MATLAB 一维随机变量及其概率分布

1、两点分布

clc
clear
a=rand(1,10);
for ii=1:10
    if a(ii)<0.2
        a(ii)=0;
    else
        a(ii)=1;
    end
end
a

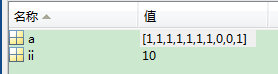
x=0的概率为0.2，x=1的概率为0.8；两点分布

clc
clear
a=rand(1,10);
b=(a>0.2)

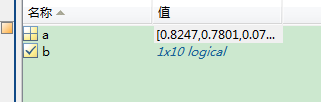
循环用向量化表示　　

2、伯努利分布（二项分布）

clc
clear
N=1000000;
r=binornd(19,0.3,1,N);%A事件发生概率0.3，重复19次。事件A发生的次数。仿真100000次
subplot(311)
hist(r);%将r等间隔的分成10个范围，y轴为该范围内的元素个数
subplot(312)
hist(r,20);%等间隔的分成20份
subplot(313)
x=0:19;
hist(r,x);%按x中元素指定的位置为中心，r的分布情况

x=0:19;
y=hist(r,x);
y(6)/N%仿真，事件发生5次的概率
p=binopdf(5,19,0.3)%调用公式计算出的事件发生五次的概率,确切值

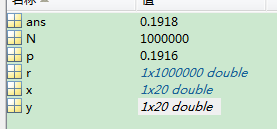
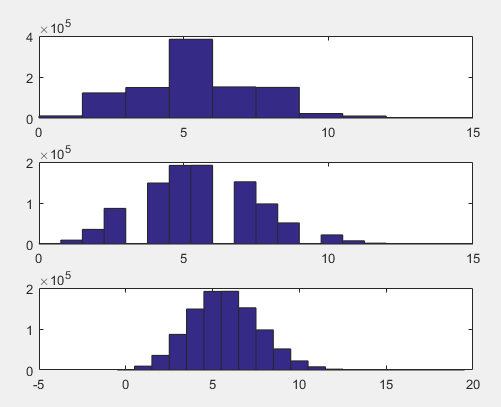
3、泊松分布

（1）泊松分布随lamda的变化

clc
clear
tic
n=0:6;
r=poissrnd(0.6,1,10000);
a=hist(r,n);
subplot(221),stem(n,a);
xlabel('k')
ylabel('p(X=k)')
title('lamda=0.6')
grid on

n=0:10;
r=poissrnd(2,1,10000);
a=hist(r,n);
subplot(222),stem(n,a);
xlabel('k')
ylabel('p(X=k)')
title('lamda=2')
grid on

n=0:20;
r=poissrnd(6,1,10000);
a=hist(r,n);
subplot(223),stem(n,a);
xlabel('k')
ylabel('p(X=k)')
title('lamda=6')
grid on

n=0:30;
r=poissrnd(14,1,10000);
a=hist(r,n);
subplot(224),stem(n,a);
xlabel('k')
ylabel('p(X=k)')
title('lamda=14')
grid on
time=toc

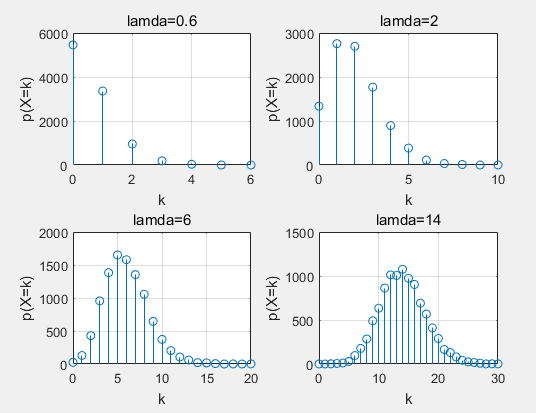
可以看到，随着lamda的变大，泊松分布越来越接近正态分布同理，计算泊松分布概率密度命令是poisspdf。

4、等可能分布

clc
clear
tic
N=100000;
s=zeros(1,N);
r1=randi([111,130],1,N);
r2=randi([56,65],1,N);
r3=randi([66,70],1,N);
r4=randi([121,130],1,N);
s=r1+r2+r3+r4;
n=length(find(s>365));
p=n/N;
time=toc

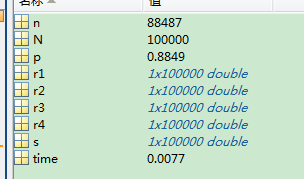
5、连续均匀分布

6、正态分布

（1）

标准正态分布

均值0.5，标准差为2 的正态分布（非方差）

方差为0.1，均值变化的正态分布

均值，方差都改变的正态分布

（2）

P{-3<ξ<3}=0.997

准确值

7、随机变量的数字特征

7.1均值

7.2

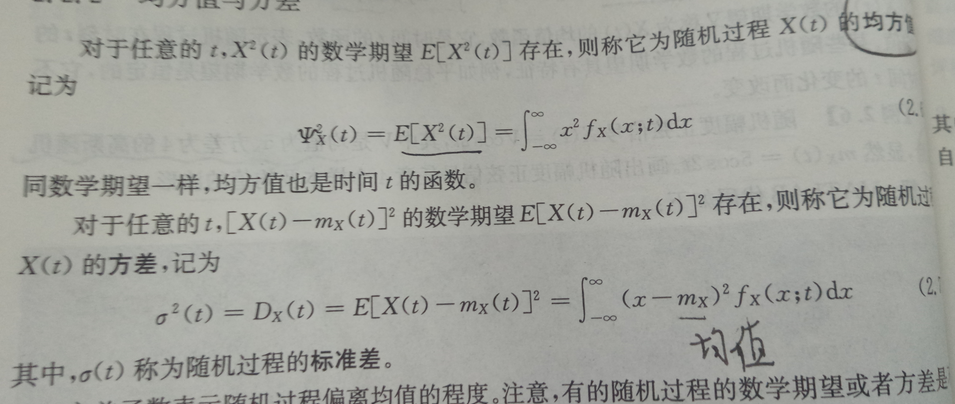
注意均方值和方差是不一样的

%随机幅度正弦信号，想x(t)=v*cos(2t),v是均值为5，方差为4的高斯随机函数
clc
clear

v=normrnd(5,2,1,2);
n=0:0.1:5;
x1=v(1)*cos(2*n);
x2=v(2)*cos(2*n);
plot(n,x1,'--',n,x2,'-.')

hold on
x=5*cos(2*n)
plot(n,x,'o-')
grid on
legend('样本1','样本2','期望信号')

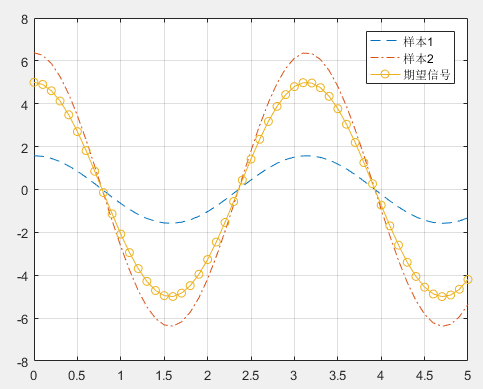
7.3

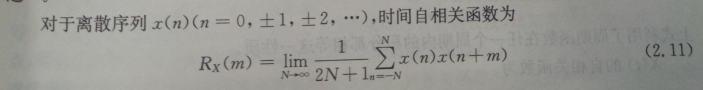
x1和x2相乘，构成了一个新的函数，该新的函数会有新的概率值，即f(x1,x2;t1,t2)。然后计算新的函数的均值。

7.4协方差

协方差用于衡量两个变量的总体误差。而 方差是协方差的一种特殊情况，即当两个变量是相同的情况。

期望值分别为 E[ X]与 E[ Y]的两个实随机变量 X与 Y之间的 协方差 Cov(X,Y)定义为：

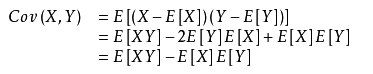
如果两个变量的变化趋势一致，也就是说如果其中一个大于自身的期望值时另外一个也大于自身的期望值，那么两个变量之间的协方差就是正值；如果两个变量的变化趋势相反，即其中一个变量大于自身的期望值时另外一个却小于自身的期望值，那么两个变量之间的协方差就是负值。

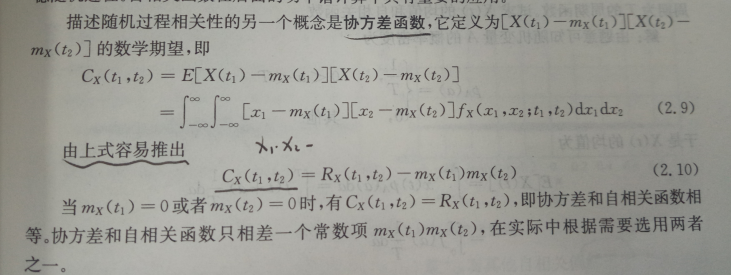
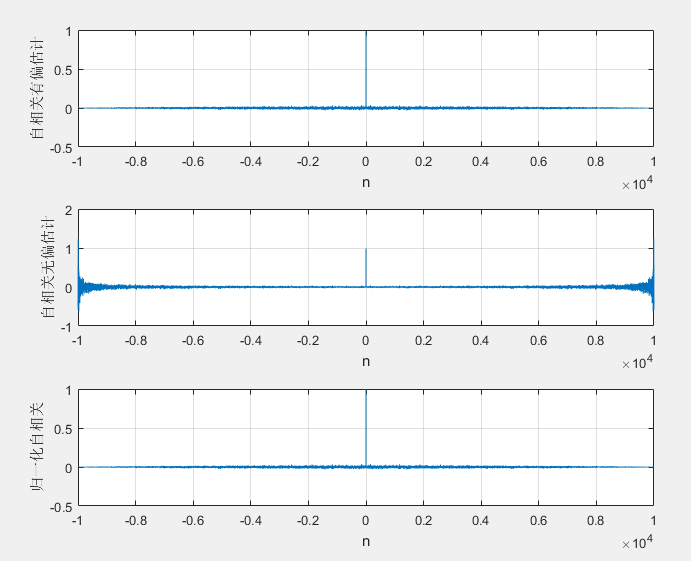
clc
clear

N=10000;
n=-(N-1):(N-1);
signal=randn(1,N);
correlation_1=xcorr(signal,'biased');
correlation_2=xcorr(signal,'unbiased');
correlation_3=xcorr(signal,'coeff');
subplot(311),plot(n,correlation_1)
xlabel('n');ylabel('自相关有偏估计');
grid on
subplot(312),plot(n,correlation_2)
xlabel('n');ylabel('自相关无偏估计');
grid on
subplot(313),plot(n,correlation_3)
xlabel('n');ylabel('归一化自相关');
grid on

7.5