Codeforces 590 A：Median Smoothing

A. Median Smoothing

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

A schoolboy named Vasya loves reading books on programming and mathematics. He has recently read an encyclopedia article that described the method of median smoothing (or median filter) and its
many applications in science and engineering. Vasya liked the idea of the method very much, and he decided to try it in practice.

Applying the simplest variant of median smoothing to the sequence of numbers a1, a2, ..., an will
result a new sequence b1, b2, ..., bnobtained
by the following algorithm:

• b1 = a1, bn = an,
  that is, the first and the last number of the new sequence match the corresponding numbers of the original sequence.
• For i = 2, ..., n - 1 value bi is
  equal to the median of three values ai - 1, ai and ai + 1.

The median of a set of three numbers is the number that goes on the second place, when these three numbers are written in the non-decreasing order. For example, the median of the set 5, 1, 2 is
number 2, and the median of set 1, 0, 1 is equal to 1.

In order to make the task easier, Vasya decided to apply the method to sequences consisting of zeros and ones only.

Having made the procedure once, Vasya looked at the resulting sequence and thought: what if I apply the algorithm to it once again, and then apply it to the next result, and so on? Vasya tried a couple of examples and found out that after some number of median
smoothing algorithm applications the sequence can stop changing. We say that the sequence is stable, if it does not change when the median smoothing is applied to it.

Now Vasya wonders, whether the sequence always eventually becomes stable. He asks you to write a program that, given a sequence of zeros and ones, will determine whether it ever becomes stable. Moreover, if it ever becomes stable, then you should determine
what will it look like and how many times one needs to apply the median smoothing algorithm to initial sequence in order to obtain a stable one.

Input

The first input line of the input contains a single integer n (3 ≤ n ≤ 500 000) —
the length of the initial sequence.

The next line contains n integers a1, a2, ..., an (ai = 0 or ai = 1),
giving the initial sequence itself.

Output

If the sequence will never become stable, print a single number  - 1.

Otherwise, first print a single integer — the minimum number of times one needs to apply the median smoothing algorithm to the initial sequence before it becomes is stable. In the second line print n numbers
separated by a space  — the resulting sequence itself.

Sample test(s)

input

4
0 0 1 1

output

0
0 0 1 1

input

5
0 1 0 1 0

output

2
0 0 0 0 0

Note

In the second sample the stabilization occurs in two steps: ,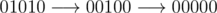
and the sequence 00000 is obviously stable.

题意是给出了一段 0 1 组成的波，然后这个波的值可能会发生变化，排除起点与终点，如果某一位置上的值不等于其左右位置加上自己的中位数话，那么它会变成中位数，这样导致波会振荡一次，问波最终是否会稳定，不会输出-1。会，就输出其振荡次数与最终波的值。

首先可以判断最终波是一定会稳定的，不可能最终不稳定，因为只有0与1，边缘值a1与an不变了，所以他们只会往中间延伸这种稳定的状态，然后我做的方法是叠加，如果前者不稳定，那么后者的不稳定程度+1，其实这么做是不对的，波振荡的这一系列的值只可能是一个山峰形状的，如1 2 1 或者 1 2 2 1.但是因为都是 0 1组成所以不用管那么多，只需管每一位置振荡次数的奇偶即可。然后就是判断每一段振荡最终位置的值，奇数不用管了，1
2 3 4 5和1 2 3 2 1最终形成的效果是一样的。偶数需要调整，1 2 3 4要调整为 1 2 2 1这样的效果。

代码：

#include <iostream>
#include <algorithm>
#include <cmath>
#include <vector>
#include <string>
#include <cstring>
#pragma warning(disable:4996)
using namespace std;

int n;
int a[5];
int val[500005];
int stable[500005];

int main()
{
    //freopen("i.txt", "r", stdin);
    //freopen("o.txt", "w", stdout);

    int i, k, maxn;
    scanf("%d", &n);

    for (i = 0; i < n; i++)
        scanf("%d", val + i);

    maxn = 0;
    memset(stable, 0, sizeof(stable));

    for (i = 1; i < n - 1; i++)
    {
        a[0] = val[i - 1];
        a[1] = val[i];
        a[2] = val[i + 1];

        sort(a, a + 3);

        if (val[i] != a[1])
        {
            stable[i] = stable[i - 1] + 1;
            maxn = max(maxn, stable[i]);
        }
        else
        {
            stable[i] = 0;
        }
    }
    int flag = 0;
    for (i = n - 2; i >= 1; i--)
    {
        if (stable[i] == 0)
        {
            flag = 0;
        }
        else
        {
            if (flag == 0 && stable[i])
            {
                flag = 1;
                if (stable[i] % 2 == 0)
                {
                    int temp = stable[i];
                    for (k = temp; k > temp / 2; k--)
                    {
                        stable[i]++;
                        i--;
                    }
                    i++;
                }
            }
        }
    }

    printf("%d\n", (maxn + 1) / 2);
    for (i = 0; i < n; i++)
    {
        if (i == 0)
        {
            printf("%d", val[i]);
        }
        else
        {
            if (stable[i] & 1)
            {
                printf(" %d", (val[i] + 1) & 1);
            }
            else
            {
                printf(" %d", val[i]);
            }
        }
    }
    printf("\n");
    //system("pause");
    return 0;
}

版权声明：本文为博主原创文章，未经博主允许不得转载。