【摩天大楼平地起】基础篇 09 简述N种查找算法

引言

　　在开始之前首先可以先思考一下假如没有查找算法会是什么情况？所有数据结构都需要全部遍历一遍，每次都一遍又一遍的查，从本质而言查找算法就是为了提高效率。

　　经过前人一代又一代的努力，目前的查找算法大致可以分为静态查找和动态查找。从名字上就很容易理解，静态查找通俗而言就是查找的时候数据不变，而动态查找也可以理解为查找的时候数据发生了改变。

　　所以这就衍生了个推论，即静态查找和动态查找算法不能通用，或者说在静态算法中使用动态算法不划算。

　　还可以从顺序的维度来划分，可以划分为无序查找和有序查找。当然其中的顺序是相对的，也就是说是依据某个参照物来比是有序或者无序。

　　平时大多数开发人员所编写的代码基本都是顺序查找，也就是说O(n)操作。

　　接下去就让我们站在前人的肩膀上，改进一下我们的思路吧。

二分查找

　　二分查找，平时在工作中应该或多或少都有听说过，这也算是除了顺序查找以外，最容易想到的查找算法了。

　　核心思路就是不断的除2，直到找到为止，就类似于以前电视节目里面的猜价格，每次猜中间的值。

　　但是这个算法前提就是给定的数据必须是有序的，如果无序的话，就没有办法决定是选上半截的中间值或是选下半截的中间值了。

　　在这里贴上一张与顺序查找的对比图：

　　

　　代码实现：

　　

  public class BinarySearch
     {
         public static int Demo(List<int> data, int key)
         {
             int low = , mid = ;
             int high = data.Count - ;
             while (low <= high)
             {
                 mid = (low + high) / ;
                 if (data[mid] == key)
                 {
                     return mid;
                 }
                 else if (data[mid] > key)
                 {
                     high = mid - ;
                 }
                 else if (data[mid] < key)
                 {
                     low = mid + ;
                 }
             }
             return -;
         }
     }

BinarySearch

　　使用场景：

　　.net已经提供的二分实现：BinarySearch

　　二分法适用于数据较为连续较为均匀的，如内存地址，索引等

　　算法复杂度 O(logn)

斐波那契查找

　　提到斐波那契，具有大学经历的小伙伴一定不会陌生，第一反应肯定就是斐波那契数列，而斐波那契查找可能有些小伙伴就没有听过了。

　　其实这个查找就是利用了斐波那契的黄金比例来减少分的次数。可以理解为是二分法的一个优化。

　　ps:没有找到gif，来个png先顶上（捂脸）

　　

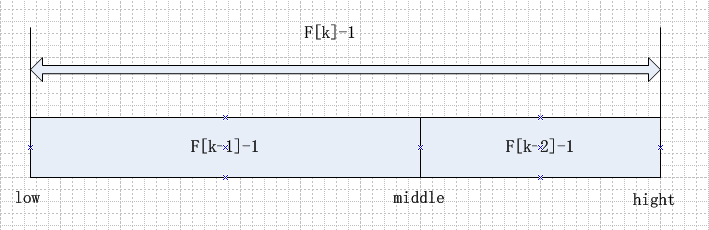
　　从图中可以看到斐波那契查找改变的是如何切分数据的问题。

　　代码如下：

  public class FibonacciSearch
     {
         public static int Demo(List<int> data, int key)
         {
             int low = ;
             int high = data.Count - ; 

             var myFibonacciSearch = new List<int>(new int[]);
             myFibonacciSearch[] = ;
             myFibonacciSearch[] = ;
             for (int i = ; i < myFibonacciSearch.Count; ++i)
             {
                 myFibonacciSearch[i] = myFibonacciSearch[i - ] + myFibonacciSearch[i - ];
             }

             int relativePosition = ;
             while (data.Count > myFibonacciSearch[relativePosition] - )
             {
                 ++relativePosition;
             }
             int[] temp = new int[myFibonacciSearch[relativePosition] - ];
             data.CopyTo(temp);

             for (int i = data.Count; i < myFibonacciSearch[relativePosition] - ; ++i)
             {
                 temp[i] = data[data.Count - ];
             }

             while (low <= high)
             {
                 int mid = low + myFibonacciSearch[relativePosition - ] - ;
                 if (key < temp[mid])
                 {
                     high = mid - ;
                     relativePosition -= ;
                 }
                 else if (key > temp[mid])
                 {
                     low = mid + ;
                     relativePosition -= ;
                 }
                 else
                 {
                     if (mid < data.Count)
                     {
                         return mid;
                     }
                     else
                     {
                         return data.Count - ;
                     }
                 }
             }
             return -;
         }
     }

FibonacciSearch

　　算法复杂度 O(logn)

插值查找

　　这个可能一般的小伙伴没有听过这个查找算法，其实这个算法也是定义了如何去找。

　　可以类比为查找字典的时候我们找X开头的单词总是会从后面开始找而找B开头的则会从头开始找。

　　插值查找就是定义了这么一个规则，通过公式    搜索键值 = left + parseInt( ( key - data[left] ) / ( data[right] - data[left] ) )*( right - left ) )

　　然后不停的切分，直到找到所需要的内容。

　　下面附上维基百科里提供的JS程序段，感兴趣的可以翻译为自己常用的语言。

　　

 var interpolationSearch = function(data, key){
     var left = ;
     var right = data.length - ;
     var m = ;
     while(left <= right){
         var m = parseInt((right - left)*(key - data[left])/(data[right] - data[left])) + left;
         if( m < left || m > right)
             break;
         if(key < data[m])
             right = m - ;
         else if(key > data[m])
             left = m + ;
         else
             return m;
     }
     return -;
 };

 //執行
 var data = getRandomData();
 quickSort(data, , data.length-);
 interpolationSearch(data, );        // (data, key)

interpolationSearch

分块查找

　　顺序查找的增强版，有点桶排序的味道。

　　分开查找的要求就是分成N块每块内部可以无序但是块与块之间必须有序。

　　这个就可以利用cpu的并行并发进行查找加速。

　　如下图所示：

　　

　　

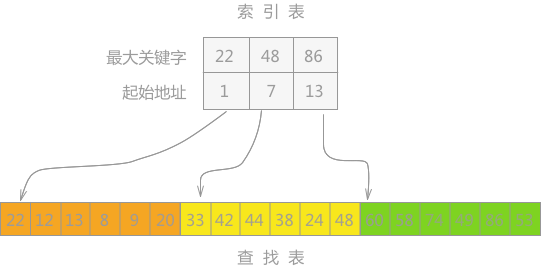
哈希查找

　　哈希对于各位开发小伙伴一定不陌生，哈希查找目的也很简单就是用空间来换时间。

　　1)       用给定的哈希函数构造哈希表；

　　2)       根据选择的冲突处理方法解决地址冲突；

　　3)       在哈希表的基础上执行哈希查找。

　　实用场景也很多：

　　1.文件查找

　　　　比如百度网盘秒传功能，适用诸如sha256等哈希算法就可以快速的找到文件是否存在（md5冲突率相对较高，不适合用做文件判重）

　　2.网络通信（微信消息算法）

　　　　数据中组装一个随机的int值然后再组装所需要的参数如id 组装成long，即后半截有序前半截随机，再使用基数对比法，只对比后部分。最终实现数据不重复的情况下查找id

　　　　用图解释就是

　　　　

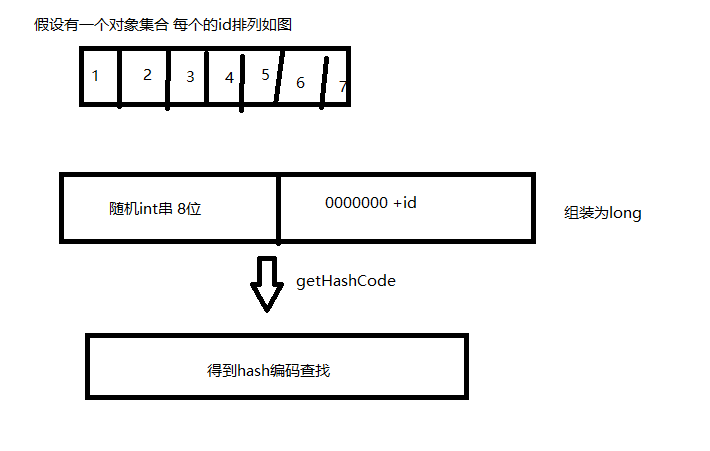
　　　　有点类似于雪花算法的感觉。

树查找

　　.net提供了教科书式的用法 感兴趣可以自行查看core源码中的SortedDictionary

　　二叉树的查询性能还行，平均查询是O(Logn),但是最坏的情况会退化为O(n),在二叉树的基础上,

　　又出来什么AVL,2-3-4,2-3(就是红黑,准确说 红黑树是2-3树的简单高效的实现)等等.

　　而B/B+平衡树其实是2-3查找树的扩展,在文件系统中好用. 所以树而言,只管用,你自己的实现根本跟不上大佬们的性能.