Circles of Waiting

题目传送门

很容易列出期望的方程,高斯消元搞一波
但是常规消元复杂度是$O(r^6)$的
考虑从左到右从上到下编号
然后按编号从小到大消元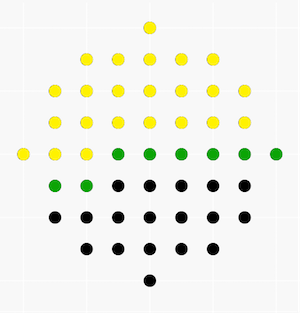

假设黄点是已经消元的点,那么消下一个点的时候,只有绿点的方程中该项系数不为0
同时,该点的方程中也只有绿点的那些项的系数不为0
由于绿点的个数是$O(r)$的,那么每次消元的复杂度就是$O(r^2)$的
总体消元复杂度就是$O(r^4)$的
然后现在得到了上三角矩阵
由于只需要求$(0,0)$点的值
所以只需要把那一行的其它元消掉
这个的复杂度也是$O(r^4)$的
总体复杂度是$O(r^4)$

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90

#include<bits/stdc++.h> #define fi first #define se second using namespace std; typedef long long LL; typedef pair<int, int> P; const int mod = 1e9 + 7; const int maxn = 8005; int add(int x, int y) { x += y; 大专栏  Circles of Waiting"line"> if(x >= mod) x -= mod; return x; } int mul(int x, int y) { LL z = 1LL * x * y; return z - z / mod * mod; } int powt(int a, int b) { int r = 1; while(b) { if(b & 1) r = mul(r, a); a = mul(a, a); b >>= 1; } return r; } int f[maxn][maxn]; int id[111][111], a[4], dx[4] = { -1, 0, 1, 0}, dy[4] = {0, -1, 0, 1}; vector<int> c; int main() { #ifdef CX_TEST freopen("E:\program--GG\test_in.txt", "r", stdin); #endif int n = 0, r, i, j, k, x, y, u, v; scanf("%d", &r); for(i = j = 0; i < 4; i++) { scanf("%d", &a[i]); j += a[i]; } j = powt(j, mod - 2); for(i = 0; i < 4; i++) a[i] = mod - mul(a[i], j); for(i = -r; i <= r; i++) { for(j = -r; j <= r; j++) { if(i * i + j * j <= r * r) id[i + 55][j + 55] = ++n; } } for(i = -r; i <= r; i++) { for(j = -r; j <= r; j++) { if(u = id[i + 55][j + 55]) { f[u][0] = f[u][u] = 1; for(k = 0; k < 4; k++) { x = i + dx[k]; y = j + dy[k]; if(v = id[x + 55][y + 55]) f[u][v] = a[k]; } } } } for(i = 1;i <= n; i++) { u = min(n, i + r * 2 + 1); c.clear(); c.push_back(0); for(j = i;j <= u; j++) { if(f[i][j]) c.push_back(j); } for(j = i + 1;j <= u; j++) { if(f[j][i]) { v = mul(mod - f[j][i], powt(f[i][i], mod - 2)); for(auto e:c) f[j][e] = add(f[j][e], mul(f[i][e], v)); } } } u = id[55][55]; for(i = 1;i <= n; i++) { if(i == u) continue; if(f[u][i]) { v = mul(mod - f[u][i], powt(f[i][i], mod - 2)); for(j = 0;j <= n; j++) f[u][j] = add(f[u][j], mul(f[i][j], v)); } } v = powt(f[u][u], mod - 2); printf("%dn", mul(f[u][0], v)); return 0; }