[CQOI2014]数三角形 题解(找规律乱搞)

题面

其实这道题不用组合数！不用容斥！

只需要一个gcd和无脑找规律（滑稽

乍一看题目，如果单纯求合法三角形的话情况太多太复杂，我们可以从局部入手，最终扩展到整体。

首先考虑这样的情况：

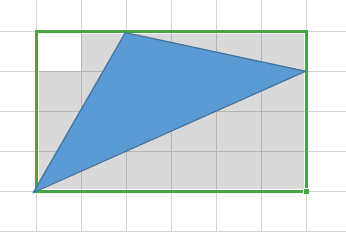
类似地，我们把三角形三个顶点都在网格边界上，且网格内任意一条线都可以把三角形切成两部分的情况，称为完全覆盖。

下面这种就不算：

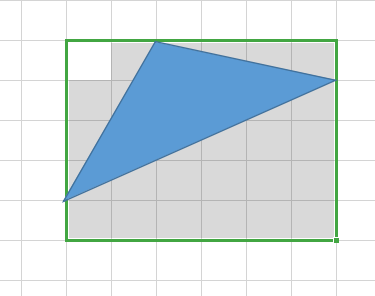
不难发现每个顶点在格点上的三角形，都有且仅有一个被它完全覆盖的网格。
所以可将原问题转化为：求出矩形中所有子矩形的完全覆盖三角形数。

又因为完全覆盖三角形数只与子矩形大小有关，与其位置无关，

而且手模一下可以发现

一个$nm$的矩形内，大小为$ij$的子矩形个数为$(n-i+1)*(m-j+1)$。

所以接下来只要求解一定长宽矩形内 完全覆盖三角形的的个数即可

然后观察可得 (迄今为止我似乎没有用除了观察之外的方法证明过东西)

如果三角形XYZ完全覆盖矩形ABCD，那么它至少有一端点在ABCD的角上。

那么接下来就可以按照 XYZ有几个端点在矩形角上分类讨论。
设矩形长为i，宽为j。

• 一个端点在角上

角的选择有4种，三角形另外两端点必在两边上，共有$(i-1)*(j-1)$种。

所以这部分答案为$4*(i-1)*(j-1)$

• 两个端点在角上

第一种：

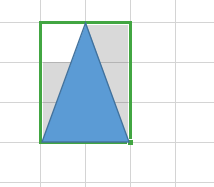
答案:\(i-1\)

第二种：

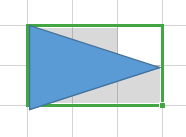
答案:\(j-1\)

第三种：

三角形有一条边与矩形对角线重合。

此时三角形剩下那个端点除了四个角以及它的对边上的格点之外，可以随便放。
那么这条对边(即矩形的一条对角线)上有几个格点呢？

$gcd(i,j)-1$个。(不包括对边的两个端点)

答案:\((i+1)*(j+1)-4-gcd(i,j)+1\)

• 三个端点在角上

显然4种。

另外，以上三种情况都可以对称过去得到不同的方案，所以$*2$。

化简可得$ans=6ij-2*gcd(i,j)$

复杂度：\(O(mnlog^{m+n})\)

#include<cstdio>
#include<iostream>
#include<cstring>
using namespace std;
typedef long long ll;
ll m,n;
int gcd(int x,int y)
{
	if(!y)return x;
	return gcd(y,x%y);
}
int main()
{
	scanf("%lld%lld",&m,&n);
	ll ans=0;
	for(int i=1;i<=n;i++)
		for(int j=1;j<=m;j++)
			ans+=(6*i*j-2LL*gcd(i,j))*(n-i+1)*(m-j+1);
	cout<<ans<<endl;
	return 0;
}

本文主要参考：https://www.luogu.org/blog/suwakow/solution-p3166