hdu 6053: TrickGCD (2017 多校第二场 1009） 【莫比乌斯 容斥原理】

题目链接

定义f[n]表示n是最大公约数情况下的计数，F[n]为n是公约数情况下的计数

（可以和 http://www.cnblogs.com/Just--Do--It/p/7197788.html hdu1695 进行类比）

显然F[n]和f[n]是满足下面这个关系的

所以，可以用下面这个公式求解f[n]

　　

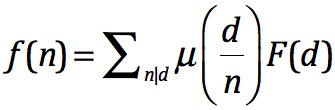
得到下面的AC代码

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;

#define max(a,b) ((a)>(b)? (a):(b))
#define min(a,b) ((a)<(b)? (a):(b))

const int maxn=1e5+;
int prime[maxn+];
bool check[maxn+];
int mu[maxn+];

void init()
{
    mu[]=;
    int tot=;
    for(int i=;i<=maxn;i++)
    {
        if(!check[i])
        {
            prime[tot++]=i;
            mu[i]=-;
        }
        for(int j=;j<tot;j++)
        {
            if(i*prime[j]>maxn) break;
            check[i*prime[j]]=true;
            if(i%prime[j]==)
            {
                mu[i*prime[j]]=;
                break;
            }
            else
            {
                mu[i*prime[j]]=-mu[i];
            }
        }
    }
}

const int N=1e5+;
const int mod=1e9+;

int n;
int num[*N];
LL F[N];
LL f[N];

LL qpow(LL x,LL n)
{
    LL ret=;
    for(;n;n>>=)
    {
        if(n&) ret=ret*x%mod;
        x=x*x%mod;
    }
    return ret;
}

int main()
{
    init();
    int T;
    scanf("%d",&T);
    for(int kase=;kase<=T;kase++)
    {
        memset(num,,sizeof(num));
        memset(f,,sizeof(f));
        int max_gcd=1e9,max_a=;
        LL ans=;
        scanf("%d",&n);
        for(int i=;i<n;i++)
        {
            int t;
            scanf("%d",&t);
            num[t]++;
            max_gcd=min(t,max_gcd);
            max_a  =max(t,max_a  );
        }
        for(int i=;i<*N;i++)
            num[i]+=num[i-];
        for(int i=;i<=max_gcd;i++)
        {
            F[i]=;
            for(int j=i;j<=max_a;j+=i)
                F[i]=F[i]*qpow(j/i,num[j+i-]-num[j-])%mod;
        }
//        =================================
        for(int i=;i<=max_gcd;i++)
            for(int j=;i*j<=max_gcd;j++)
                f[i]=(f[i]+mu[j]*F[i*j])%mod;
        for(int i=;i<=max_gcd;i++)
            ans=(ans+f[i])%mod;
//        =================================
        printf("Case #%d: %lld\n",kase,ans);
    }
}

然而！=====所夹的部分可以用一行代码代替！！！！虽然运行时间不会减少多少，不过代码量上优化了很多！

不过这种写法的实质其实可以从容斥原理的角度来考虑，再借用了莫比乌斯函数的性质。

定义：  性质P_i表示i是对象x的一个质因数，　　集合A_i表示具有性质P_i的对象的集合

比较容易想到，所有可能的公因数对应的对象计数之和，恰为所有集合的并 中的对象的总个数

那么用容斥原理求 所有集合的并 中的对象的总个数时，奇数个基本集合的交前面的系数是正一，偶数个的是负一。并且，n的因数中包含质因数平方的F[n]在这里面是不需要被计数的。

这样恰好就与莫比乌斯函数的性质产生了联系。

参考博客：　　http://blog.csdn.net/acterminate/article/details/76216345

也就变成了

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;

#define max(a,b) ((a)>(b)? (a):(b))
#define min(a,b) ((a)<(b)? (a):(b))

const int maxn=1e5+;
int prime[maxn+];
bool check[maxn+];
int mu[maxn+];

void init()
{
    mu[]=;
    int tot=;
    for(int i=;i<=maxn;i++)
    {
        if(!check[i])
        {
            prime[tot++]=i;
            mu[i]=-;
        }
        for(int j=;j<tot;j++)
        {
            if(i*prime[j]>maxn) break;
            check[i*prime[j]]=true;
            if(i%prime[j]==)
            {
                mu[i*prime[j]]=;
                break;
            }
            else
            {
                mu[i*prime[j]]=-mu[i];
            }
        }
    }
}

const int N=1e5+;
const int mod=1e9+;

int n;
int num[*N];
LL F[N];
LL f[N];

LL qpow(LL x,LL n)
{
    LL ret=;
    for(;n;n>>=)
    {
        if(n&) ret=ret*x%mod;
        x=x*x%mod;
    }
    return ret;
}

int main()
{
    init();
    int T;
    scanf("%d",&T);
    for(int kase=;kase<=T;kase++)
    {
        memset(num,,sizeof(num));
        memset(f,,sizeof(f));
        int max_gcd=1e9,max_a=;
        LL ans=;
        scanf("%d",&n);
        for(int i=;i<n;i++)
        {
            int t;
            scanf("%d",&t);
            num[t]++;
            max_gcd=min(t,max_gcd);
            max_a  =max(t,max_a  );
        }
        for(int i=;i<*N;i++)
            num[i]+=num[i-];
        for(int i=;i<=max_gcd;i++)
        {
            F[i]=;
            for(int j=i;j<=max_a;j+=i)
                F[i]=F[i]*qpow(j/i,num[j+i-]-num[j-])%mod;
//            printf("F[%d]=%4lld\n",i,F[i]);
            ans=(ans-mu[i]*F[i]+mod)%mod;
        }
        printf("Case #%d: %lld\n",kase,ans);
    }
}