P1040加分二叉树

据说窝回去的那几天考了n次试

过去了一个月才想起来补锅

传送

首先来区分一下什么是中序遍历，什么又是前序遍历

中序遍历：左，根，右（也就是说给出一个序列（按照中序遍历的序列），第i个点左边的点都是i的左子树，右边的点都是i 的右子树）

前序遍历：根，左，右，也就是我们平常画一棵树的顺序

因为这个题目中只给出了中序遍历的顺序，但是画出来的树可以千奇百怪

比如说：

样例可以长成这个样子

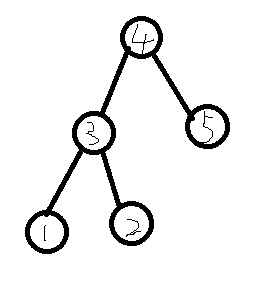
还可以长成这样子

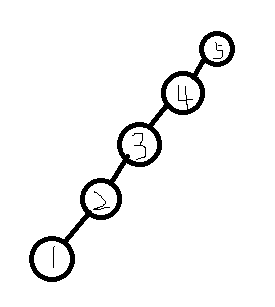
所以树的样子与树根的选择有着密切的联系

上面中序遍历中提到了一个性质：给出一个序列（按照中序遍历的序列），第i个点左边的点都是i的左子树，右边的点都是i 的右子树

仔细观察，发现这道题就是让我们对于每棵子树选出树根，使总得分最大，树根也就是上面的i。

似乎是个区间dp?窝也不知道啊，就当它是吧。

结合上面的性质，我们在枚举k（第三层枚举的断点）的时候，就相当于在枚举树根。考虑到要输出前序遍历，我们就把最终选定的树根记录下来。

我们设f[i][j]表示区间[i,j]的最大得分，root[i,j]表示区间[i,j]中选定的树根。

则：f[i][j]=max{f[i][k-1]*f[k+1][j]+f[k][k]}(i<k<j)，初始化：f[i][i]=i，root[i][i]=i，f[i][j]=f[i+1][j]=f[i][i](这里是假定左子树为空，如果左子树不为空，肯定会有更优的解覆盖掉它)

区间dp步骤：

第一层：枚举区间长度（<n）

第二层：枚举起点st(st+len<=n),计算终点end=st+len

第三层：枚举断点k(st<=k<end)

在这道题里面，由于f[st][end]初始化时就是k=st的情况,所以k直接从st+1开始

输出前序遍历：递归输出。首先输出[l,r]的根节点，再输出左子树，再输出右子树。（详情见代码）

代码：

#include<bits/stdc++.h>
#define ll long long
using namespace std;
ll n,f[][],root[][];//注意数据范围
ll read()
{
   char ch=getchar();
   ll x=;    bool f=;
   while(ch<''||ch>'')
   {
        if(ch=='-')
         f=;
        ch=getchar();
   }
   while(ch>=''&&ch<='')
   {
       x=(x<<)+(x<<)+(ch^);
       ch=getchar();
   }
   return f?-x:x;
}
void print(int l,int r)
{
    if(l>r)return;
    printf("%lld ",root[l][r]);
    if(l==r)return ;//注意顺序
    print(l,root[l][r]-);//注意这里是按照根节点分左右的
    print(root[l][r]+,r);
}
int main()
{
    n=read();
    for(int i=;i<=n;i++)
     f[i][i]=read(),root[i][i]=i;
    for(int len=;len<n;len++)
    {
        for(int st=;st+len<=n;st++)
        {
            int end=st+len;
            f[st][end]=f[st+][end]+f[st][st];
            root[st][end]=st;
            for(int k=st+;k<end;k++)
            {
                if(f[st][end]<f[st][k-]*f[k+][end]+f[k][k])
                  f[st][end]=f[st][k-]*f[k+][end]+f[k][k],root[st][end]=k;
            }
        }
    }
    printf("%lld\n",f[][n]);
    print(,n);
}