《编译原理》构造与正规式 (0|1)*01 等价的 DFA - 例题解析

《编译原理》构造与正规式 (0|1)*01 等价的 DFA - 例题解析

解题步骤：

• NFA 状态转换图
• 子集法
• DFA 的状态转换矩阵
• DFA 的状态转图

解：

已给正规式：(0|1)*01

画出 NFA 状态转换图如下：

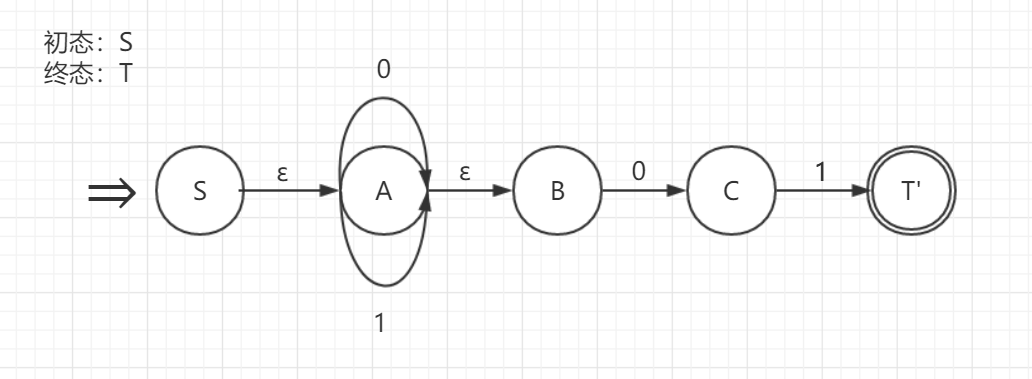
子集法的表格：

I状态\字符	I0	I1
{S, A, B} 求法： 表示开始符号，以及开始符号识别 n 个 ε 可以到达的状态集合。如本题中： 开始符号 S，通过识别 ε 可以到达的转态有 A, B，所以集合为 {S, A, B}	{A, B, C} 求法： 表示改行最左端的状态集，识别最上端的符号可以到达的状态，以及这些状态识别 n 个 ε 可以到达的状态的集合。如本题中： 有 {S, A, B}，逐个判断 S 识别 0 弧没有可以到达的状态；A 识别 0 可以到达 A，B 识别 0 可以到达 C；现在已有 A, C 状态，又因为 A 状态识别 ε 可以到达 B，所以整个集合为 {A, B, C}	{A, B} 求法： 同相邻左测表格求法。如本题中： 有 {S, A, B}，S 状态识别 1 没有可以到达的状态，A 识别 1 可以到达 A，B 识别 1 没有可以到达的状态。所以此时只有 A。又因为 A 状态识别 ε 可以到达 B，所以整个集合为 {A, B}
{A, B, C} 求法： 这个为什么是 {A, B, C}？因为 相邻右上方表格为 {A, B, C} 为什么用相邻右上方表格的状态集？因为 它是初始态，仅识别 0 和 ε 就能到达的状态集。所以，可以将该状态集视为识别一条弧所到达的状态集。可以看做是下一状态，为起状态别名做准备。	{A, B, C} 注： 有 A 就有 B	{A, B, T}
{A, B}	{A, B, C}	{A, B}
{A, B, T}	{A, B, C}	{A, B}

对状态中间重命名，求新的状态转换矩阵：

（1）因为 S 是初态，重命名为 S'，也是终态

（2）设 {A, B, C} 为 A'

（3）设 {A, B} 为 B'

（4）因为 T 是终态，此时 {A, B, T} 不是相当于 A' 识别 1 弧所到达的状态，T 是终态，{A, B, T} 也是终态，重命名为 T'

I状态\字符	I0	I1
S'	A'	B'
A'	A'	T'
B'	A'	B'
T'	A'	B'

画出 NFA 状态转换图如下：

验证

(0|1)*01 正规式对应的正规集元素特点是：

• 以 0 或 1 的任意组合，任意数量为开头
• 以 01 为结尾

当结尾为终结符时，可认为识别成功