POJ 3549 GSM phone（圆+扫描线+最短路）

题目意思是求起点s到终点s的最短路，但是只能在圆的内部和边上走。一种可以想到的方法就是求出所有的交点，然后两两连边并验证合法性，但是这样的交点数规模有n²。

我们可以观察发现，我们在圆求并构成的图形中，在其内部的点是不可能成为最短路上的点，只可能是沿着边上的点擦着经过，所以我们需要把在圆内部的所有点都给扣掉，同样可以证明这样的点的规模只有n个，接下来只需要暴力连边，但是连边的时候需要验证这样的点对是否沿着直线可达。我是直接将这条线段暴力和所有圆求交点，左侧端点计为1，右侧端点计为-1，然后用类似于扫描线的做法sort一遍，最后判断线段的两端是否被这个区间包含即可。

最后跑一边dijk就求出答案。

这个方法感觉不是很好.... 还有比我快20倍的orz... 

如果扣的是灰色点那么规模有n²

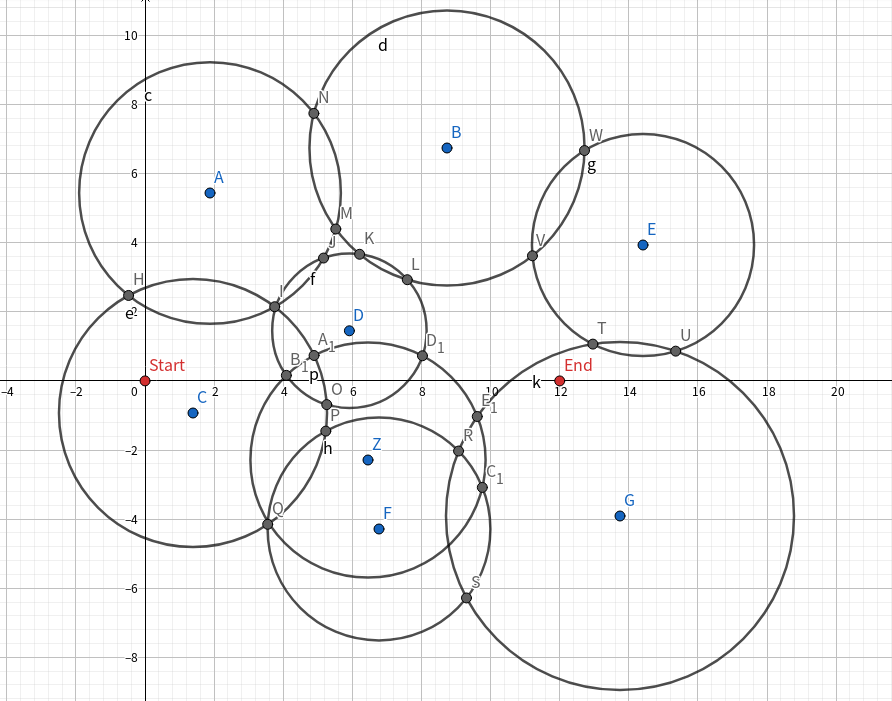
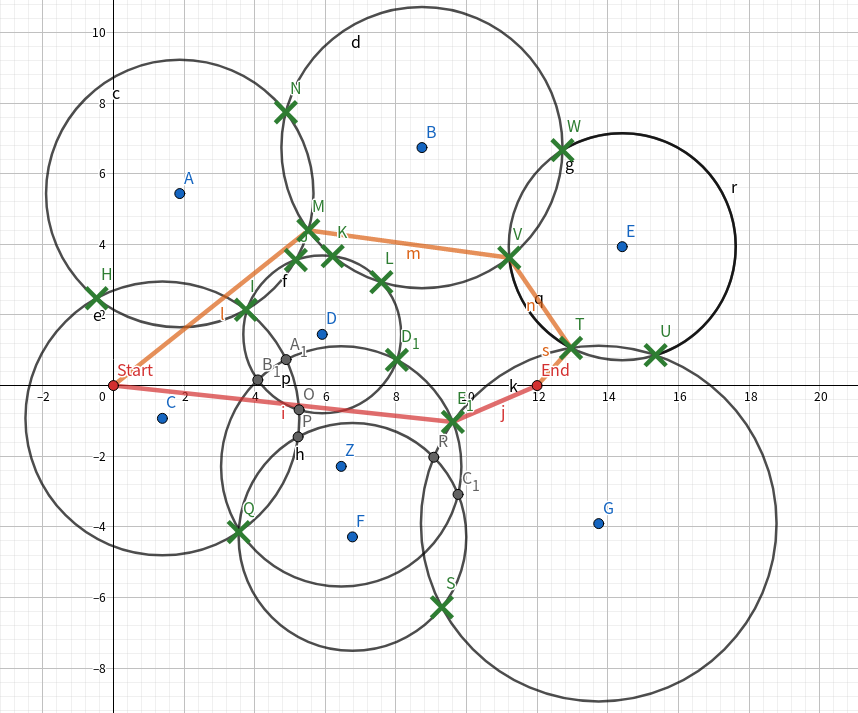
如果是外侧点只有n个，绿色点即为可用点，红色和橙色为两条路，则最短路必然擦过外侧点或者起点终点直接相连

 //      ——By DD_BOND

 //#include<bits/stdc++.h>
 //#include<unordered_map>
 //#include<unordered_set>
 #include<functional>
 #include<algorithm>
 #include<iostream>
 //#include<ext/rope>
 #include<iomanip>
 #include<climits>
 #include<cstring>
 #include<cstdlib>
 #include<cstddef>
 #include<cstdio>
 #include<memory>
 #include<vector>
 #include<cctype>
 #include<string>
 #include<cmath>
 #include<queue>
 #include<deque>
 #include<ctime>
 #include<stack>
 #include<map>
 #include<set>
 #include<cassert>

 #define fi first
 #define se second
 #define pb push_back
 #define MP make_pair

 #pragma GCC optimize(3)
 #pragma GCC target("sse,sse2,sse3,ssse3,sse4,popcnt,abm,mmx,avx,tune=native")

 using namespace std;

 typedef long double db;
 typedef long long ll;
 typedef pair<db,db> Pd;
 typedef pair<int,int> P;
 typedef pair<ll,ll> Pll;

 const db eps=1e-;
 const int MAXN=1e5+;
 const db pi=acos(-1.0);
 const ll INF=0x3f3f3f3f3f3f3f3f;

 inline int dcmp(db x){
     if(fabs(x)<eps) return ;
     return (x>? : -);
 }

 inline db Sqrt(db x){
     return x>? sqrt(x): ;
 }

 inline db sqr(db x){ return x*x; }

 struct Point{
     db x,y;
     Point(){ x=,y=; }
     Point(db _x,db _y):x(_x),y(_y){}
     void input(){
         double _x,_y;
         scanf("%lf%lf",&_x,&_y);
         x=_x,y=_y;
     }
     void output(){ printf("%.2f %.2f\n",(double)x,(double)y); }
     friend istream &operator >>(istream &os,Point &b){
         os>>b.x>>b.y;
         return os;
     }
     friend ostream &operator <<(ostream &os,Point &b){
         os<<b.x<<' '<<b.y;
         return os;
     }
     bool operator ==(const Point &b)const{
         return (dcmp(x-b.x)==&&dcmp(y-b.y)==);
     }
     bool operator !=(const Point &b)const{
         return !((dcmp(x-b.x)==&&dcmp(y-b.y)==));
     }
     bool operator <(const Point &b)const{
         return (dcmp(x-b.x)==? dcmp(y-b.y)< : x<b.x);
     }
     db operator ^(const Point &b)const{     //叉积
         return x*b.y-y*b.x;
     }
     db operator *(const Point &b)const{     //点积
         return x*b.x+y*b.y;
     }
     Point operator +(const Point &b)const{
         return Point(x+b.x,y+b.y);
     }
     Point operator -(const Point &b)const{
         return Point(x-b.x,y-b.y);
     }
     Point operator *(db a){
         return Point(x*a,y*a);
     }
     Point operator /(db a){
         return Point(x/a,y/a);
     }
     db len2(){  //长度平方
         return sqr(x)+sqr(y);
     }
     db len(){   //长度
         return Sqrt(len2());
     }
     Point change_len(db r){ //转化为长度为r的向量
         db l=len();
         if(dcmp(l)==)  return *this;  //零向量
         return Point(x*r/l,y*r/l);
     }
     Point rotate_left(){    //逆时针旋转90度
         return Point(-y,x);
     }
     Point rotate_right(){   //顺时针旋转90度
         return Point(y,-x);
     }
 };

 inline db cross(Point a,Point b){   //叉积
     return a.x*b.y-a.y*b.x;
 }

 inline db dot(Point a,Point b){ //点积
     return a.x*b.x+a.y*b.y;
 }

 inline db dis(Point a,Point b){ //两点的距离
     Point p=b-a;    return p.len();
 }

 struct Line{
     Point s,e;
     Line(){}
     Line(Point _s,Point _e):s(_s),e(_e){} //两点确定直线
     void input(){
         s.input();
         e.input();
     }
     db length(){    //线段长度
         return dis(s,e);
     }
 };

 inline db point_to_line(Point p,Line a){   //点到直线距离
     return fabs(cross(p-a.s,a.e-a.s)/a.length());
 }

 inline Point projection(Point p,Line a){       //点在直线上的投影
     return a.s+(((a.e-a.s)*dot(a.e-a.s,p-a.s))/(a.e-a.s).len2());
 }

 struct Circle{
     Point p;
     db r;
     Circle(){}
     void input(){
         p.input();
         double _r;
         scanf("%lf",&_r);
         r=_r;
     }
 };

 inline int relation(Point p,Circle a){ //点和圆的位置关系  0:圆外    1:圆上   2:圆内
     db d=dis(p,a.p);
     if(dcmp(d-a.r)==)  return ;
     return (dcmp(d-a.r)<? : );
 }

 inline int relation(Line a,Circle b){  //直线和圆的位置关系  0:相离   1:相切   2:相交
     db p=point_to_line(b.p,a);
     if(dcmp(p-b.r)==)  return ;
     return (dcmp(p-b.r)<? : );
 }

 inline int relation(Circle a,Circle v){    //圆和圆的位置关系  1:内含  2:内切  3:相交   4:外切   5:相离
     db d=dis(a.p,v.p);
     if(dcmp(d-a.r-v.r)>)   return ;
     if(dcmp(d-a.r-v.r)==)  return ;
     db l=fabs(a.r-v.r);
     if(dcmp(d-l)>)     return ;
     if(dcmp(d-l)==)    return ;
     return ;
 }

 inline int circle_intersection(Circle a,Circle v,Point &p1,Point &p2){ //两个圆的交点
     int rel=relation(a,v);                                      //返回交点个数，保存在引用中
     if(rel==||rel==)  return ;
     db d=dis(a.p,v.p);
     db l=(d*d+a.r*a.r-v.r*v.r)/(*d);
     db h=Sqrt(a.r*a.r-l*l);
     Point tmp=a.p+(v.p-a.p).change_len(l);
     p1=tmp+((v.p-a.p).rotate_left().change_len(h));
     p2=tmp+((v.p-a.p).rotate_right().change_len(h));
     if(rel==||rel==)  return ;
     return ;
 }

 inline int line_circle_intersection(Line v,Circle u,Point &p1,Point &p2){  //直线和圆的交点
     if(!relation(v,u))  return ;                                   //返回交点个数，保存在引用中
     Point a=projection(u.p,v);
     db d=point_to_line(u.p,v);
     d=Sqrt(u.r*u.r-d*d);
     if(dcmp(d)==){
         p1=a,p2=a;
         return ;
     }
     p1=a+(v.e-v.s).change_len(d);
     p2=a-(v.e-v.s).change_len(d);
     return ;
 }

 typedef pair<db,int>pdi;
 typedef pair<Point,int> pd;

 vector<pdi>edge[MAXN];

 db d[MAXN];
 pd st[MAXN];
 bool mark[MAXN];
 Circle circle[MAXN];
 Point s,t,it1,it2,inter[MAXN],point[MAXN];

 priority_queue<pdi,vector<pdi>,greater<pdi> >q;

 bool cmp(pd a,pd b){
     if(a==b)    return a.se>b.se;
     return a<b;
 }

 int main(void){
     s.input();  t.input();
     int n,m=,cnt=;  scanf("%d",&n);
     for(int i=;i<=n;i++)   circle[i].input();
     for(int i=;i<=n;i++)
         for(int j=i+;j<=n;j++){
             int p=relation(circle[i],circle[j]);
             if(p==||p==||p==){
                 circle_intersection(circle[i],circle[j],it1,it2);
                 point[m++]=it1,point[m++]=it2;
             }
         }
     sort(point+,point+m);
     m=unique(point+,point+m)-point;
     for(int i=;i<m;i++)
         for(int j=;j<=n;j++)
             if(relation(point[i],circle[j])==){
                 mark[i]=;
                 break;
             }
     for(int i=;i<m;i++)
         if(mark[i]==)
             point[cnt++]=point[i];
     m=cnt;  point[]=s,point[m]=t;
     for(int i=;i<=m;i++)
         for(int j=i+;j<=m;j++){
             int p=;
             Line l(point[i],point[j]);
             Point p1=point[i],p2=point[j];
             if(p2<p1)   swap(p1,p2);
             for(int k=;k<=n;k++){
                 Circle c=circle[k];
                 if(relation(l,c)){
                     line_circle_intersection(l,c,it1,it2);
                     if(it2<it1) swap(it1,it2);
                     st[p++]=pd(it1,);
                     st[p++]=pd(it2,-);
                 }
             }
             int found=;
             sort(st,st+p,cmp);
             for(int k=,sum=,start=;k<p;k++){
                 sum+=st[k].se;
                 if(sum==){
                     if(!(p1<st[start].fi)&&!(st[k].fi<p2)) found=;
                     start=k+;
                 }
             }
             if(found){
                 edge[i].pb(pdi(l.length(),j));
                 edge[j].pb(pdi(l.length(),i));
             }
         }
     for(int i=;i<=m;i++)   d[i]=1e20;
     q.push(pdi(,));
     while(!q.empty()){
         pdi p=q.top();  q.pop();
         if(dcmp(d[p.se]-p.fi)<)   continue;
         for(int i=;i<edge[p.se].size();i++){
             int v=edge[p.se][i].se;
             db val=edge[p.se][i].fi;
             if(dcmp(d[p.se]+val-d[v])<){
                 d[v]=d[p.se]+val;
                 q.push(pdi(d[v],v));
             }
         }
     }
     printf("%.5f\n",(double)d[m]);
     return ;
 }