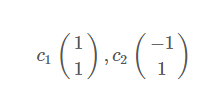PCA算法和实例
PCA算法
算法步骤:
假设有m条n维数据。
1. 将原始数据按列组成n行m列矩阵X
2. 将X的每一行(代表一个属性字段)进行零均值化,即减去这一行的均值
3. 求出协方差矩阵C=1/mXXT
4. 求出协方差矩阵的特征值以及对应的特征向量
5. 将特征向量按对应特征值大小从上到下按行排列成矩阵,取前k行组成矩阵P
6. Y=PX即为降维到k维后的数据
实例

以这个为例,我们用PCA的方法将这组二维数据降到一维
因为这个矩阵的每行已经是零均值,所以我们可以直接求协方差矩阵:
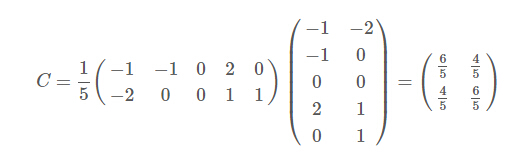
然后求其特征值和特征向量,求解后的特征值为:
λ1=2,λ2=2/5
其对应的特征向量分别是:
由于对应的特征向量分别是一个通解,c1和c2可取任意实数。那么标准化后的特征向量为:
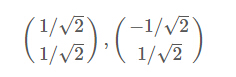
因此我们的矩阵P是:
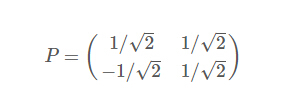
可以验证协方差矩阵C的对角化:
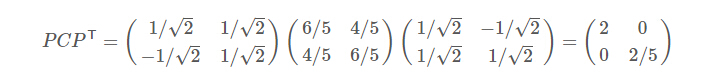
最好我们用P的第一行诚意数据矩阵,就得到了降维后的数据表示:
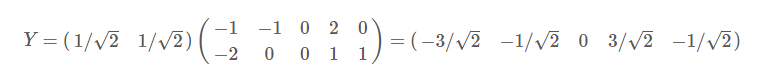
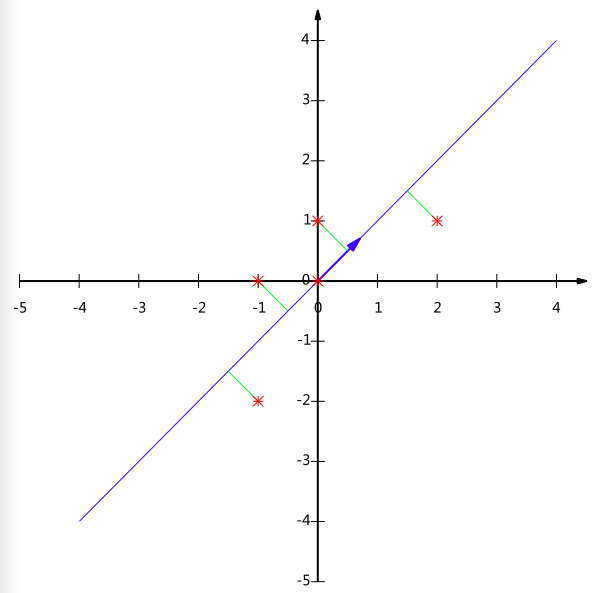
降维后的投影结果如下图:
PCA本质上是将方差最大的方向作为主要特征,并且在各个正交方向上将数据“离相关”,也就是让它们在不同的正交方向上没有相关性。
因此,PCA也存在一些限制,例如它可以很好地解除线性相关,但是对于高阶相关性就没有办法了。对于存在高阶相关性的数据,可以考虑Kernel PCA,通过Kernel将非线性相关转化为线性相关。另外,PCA假设数据各特征分布在正交方向上,如果在非正交方向上存在几个方差较大的方向,PCA的效果就大打折扣。
PCA是一种无参数技术,也就是说面对同样的数据,如果不考虑清晰,谁来做结果都一样,没有主观参数的介入,所以PCA便于通用实现,但是本身没有个性化的优化。
本文主要参考:http://blog.codinglabs.org/articles/pca-tutorial.html
PCA算法和实例的更多相关文章
- 模式识别(1)——PCA算法
作者:桂. 时间:2017-02-26 19:54:26 链接:http://www.cnblogs.com/xingshansi/articles/6445625.html 声明:转载请注明出处, ...
- PCA算法详解——本质上就是投影后使得数据尽可能分散(方差最大),PCA可以被定义为数据在低维线性空间上的正交投影,这个线性空间被称为主⼦空间(principal subspace),使得投影数据的⽅差被最⼤化(Hotelling, 1933),即最大方差理论。
PCA PCA(Principal Component Analysis,主成分分析)是一种常用的数据分析方法.PCA通过线性变换将原始数据变换为一组各维度线性无关的表示,可用于提取数据的主要特征分量 ...
- PCA算法是怎么跟协方差矩阵/特征值/特征向量勾搭起来的?
PCA, Principle Component Analysis, 主成份分析, 是使用最广泛的降维算法. ...... (关于PCA的算法步骤和应用场景随便一搜就能找到了, 所以这里就不说了. ) ...
- 三种方法实现PCA算法(Python)
主成分分析,即Principal Component Analysis(PCA),是多元统计中的重要内容,也广泛应用于机器学习和其它领域.它的主要作用是对高维数据进行降维.PCA把原先的n个特征用数目 ...
- 降维之pca算法
pca算法: 算法原理: pca利用的两个维度之间的关系和协方差成正比,协方差为0时,表示这两个维度无关,如果协方差越大这表明两个维度之间相关性越大,因而降维的时候, 都是找协方差最大的. 将XX中的 ...
- k邻近算法(KNN)实例
一 k近邻算法原理 k近邻算法是一种基本分类和回归方法. 原理:K近邻算法,即是给定一个训练数据集,对新的输入实例,在训练数据集中找到与该实例最邻近的K个实例,这K个实例的多数属于某个类,就把该输入实 ...
- PCA算法学习(Matlab实现)
PCA(主成分分析)算法,主要用于数据降维,保留了数据集中对方差贡献最大的若干个特征来达到简化数据集的目的. 实现数据降维的步骤: 1.将原始数据中的每一个样本用向量表示,把所有样本组合起来构成一个矩 ...
- OpenCV学习(35) OpenCV中的PCA算法
PCA算法的基本原理可以参考:http://www.cnblogs.com/mikewolf2002/p/3429711.html 对一副宽p.高q的二维灰度图,要完整表示该图像,需要m = ...
- 我所认识的PCA算法的princomp函数与经历 (基于matlab)
我接触princomp函数,主要是因为实验室的项目需要,所以我一接触的时候就希望快点学会怎么用. 项目中需要利用PCA算法对大量数据进行降维. 简介:主成分分析 ( Principal Compone ...
随机推荐
- 13DBUtils工具类
如果只使用JDBC进行开发,我们会发现冗余代码过多,为了简化JDBC开发,本案例我们讲采用apache commons组件一个成员:DBUtils. DBUtils就是JDBC的简化开发工具包.需要项 ...
- 如何把word文档内容和图片直接导入到wordpress编辑器
Chrome+IE默认支持粘贴剪切板中的图片,但是我要发布的文章存在word里面,图片多达数十张,我总不能一张一张复制吧?Chrome高版本提供了可以将单张图片转换在BASE64字符串的功能.但是无法 ...
- 容易混淆的JavaScript基础知识之语法部分
type 属性: 默认的 type 就是 javascript, 所以不必显式指定 type 为 javascript javascript 不强制在每个语句结尾加 “:” , javascript ...
- Linux系统判断当前运行的 Apache 所使用的配置文件
问题描述 由于历史备份.更新等原因,导致在 Linux 系统服务器中存在多个 Apache目录,如果不是网站的配置人员,可能会不清楚应该修改哪个配置文件进行网站调整. 解决方案 可以通过如下步骤,判断 ...
- 使用随机森林实现OSM路网城市多车道信息提取
Multilane roads extracted from the OpenStreetMap urban road network using random forests.,DOI:10.111 ...
- CF1182 D Complete Mirror——思路
题目:http://codeforces.com/contest/1182/problem/D 很好的思路是从度数为1的点和直径来入手. 找一条直径.看看直径的两个端点是否合法. 如果都不合法,那么根 ...
- php Closure类 闭包 匿名函数
php匿名函数 匿名函数就是没有名称的函数.匿名函数可以赋值给变量,还能像其他任何PHP对象那样传递.不过匿名函数仍是函数,因此可以调用,还可以传入参数.匿名函数特别适合作为函数或方法的回调. 如: ...
- android7.0对于SharedPreferences设置模式的限制
错误信息: 03-28 10:16:12.701 830 932 E AndroidRuntime: FATAL EXCEPTION: Thread-903-28 10:16:12.701 ...
- Integer自动装箱和拆箱
Integer a=3; => Integer a=Integer.valueOf(3); /** *@description: 自动装箱和拆箱 *@auther: yangsj *@ ...
- Grafana+Prometheus系统监控之Redis
REmote DIctionary Server(Redis) 是一个由Salvatore Sanfilippo写的key-value存储系统. Redis是一个开源的使用ANSI C语言编写.遵守B ...