Codeforces 1172B(组合数学)

题面

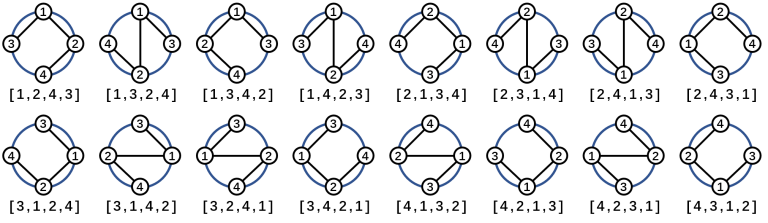
给出一棵n个点的树，要求把它画在圆上，且边不相交，画法与排列一一对应(即旋转后相同的算不同种)，求方案数。如下图是4个点的树\(T:V=\{1,2,3,4\},E=\{(1,2),(1,3),(2,4)\}\)的方案:

图片来自cf原题

分析

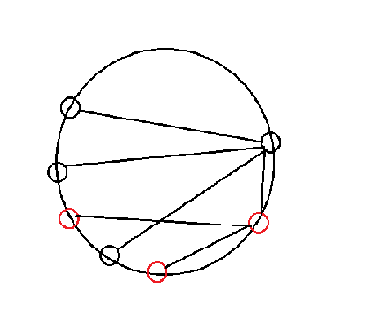
对于x的子树，我们发现x的子树上的节点在圆上一定是一个连续区间，否则会出现下图的情况

设deg[x]表示x的度数

对于非根节点x:

x有deg[x]-1个儿子，这些儿子排列的方案有\((deg[x]-1)!\)种，然后把根节点插到儿子与儿子相邻的任意一个位置，一共deg[x]个空，总答案为\((deg[x]-1)! \times deg[x]=deg[x]!\)

对于根节点x:

x本身的位置可以在圆上任选，有n种.x有deg[x]个儿子，排列方案为\(n \times deg[x]!\)

因此，总方案数为\(n \times\prod_{i=1}^n deg(i)!\)

代码

#include<iostream>
#include<cstdio>
#define maxn 200005
#define mod 998244353
using namespace std;
int n;
long long fact[maxn];
int deg[maxn];

int main(){
	int u,v;
	scanf("%d",&n);
	for(int i=1;i<n;i++){
		scanf("%d %d",&u,&v);
		deg[u]++;
		deg[v]++;
	}
	fact[0]=1;
	for(int i=1;i<=n;i++){
		fact[i]=fact[i-1]*i%mod;
	}
	long long ans=1;
	for(int i=1;i<=n;i++){
		ans*=fact[deg[i]];
		ans%=mod;
	}
	ans*=n;
	ans%=mod;
	printf("%I64d\n",ans);
}