2020牛客暑期多校训练营（第一场）Easy Integration

传送门：J. Easy Integration

题意：给你n，求这个积分，最后的结果分子是记为p，分母记为q。

求（p*q^-1）mod 998244353。

题解：比赛完看到巨巨说这是贝塔函数，我一搜还真是。

贝塔函数的递推公式：

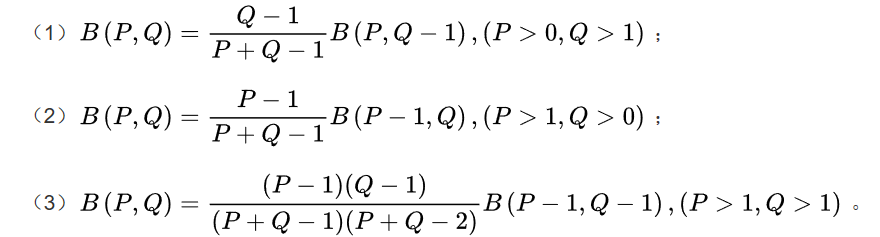
但是菜鸡只会打表找规律。那么说说怎么找到的规律吧。

先把所有的分子分母都找到，这个要用到（x-1）^n=C(n,0)x^n(-1)^0+C(n,1)x^(n-1)(-1)^1+C(n,2)x^(n-2)(-1)^2+……+C(n,n)x^0(-1)^n   ，(-1)^x 从0到n变成从n到0就变成了 (1-x)^n 的公式了。把分母都输出，发现分母是从(n+1)到(2n+1)连续的数，相乘就是 n! / (2n+1)! 。然后把分式通分，求出所有的分子相加，输出分子的和会发现分子就是 n! 。所以这个分式就是 n!*n! / (2n+1)! 。这里应该会用到费马小定理，拓展欧几里得也可以，我这里用的是费马小定理。

 1 #include<bits/stdc++.h>
 2 #define ll long long
 3 #define pb push_back
 4 #define ft first
 5 #define sd second
 6 using namespace std;
 7
 8 ll fac[2000100],inv[2000100];
 9 const ll mod=998244353;
10 const ll N=2e6+10;
11 ll a[1001000],b[1000100];
12
13 ll quick(ll a,ll b)
14 {
15     ll res=1;
16     a=a%mod;
17     while(b){
18         if(b&1) res=(res*a)%mod;
19         a=(a*a)%mod;
20         b>>=1;
21     }
22     return res%mod;
23 }
24
25 void init()
26 {
27     fac[0]=inv[0]=inv[1]=1;
28     for(ll i=1;i<=N;i++)
29         fac[i]=fac[i-1]*i%mod;
30     for(ll i=2;i<=N;i++)
31         inv[i]=(mod-mod/i)*inv[mod%i]%mod;
32     for(ll i=1;i<=N;i++)
33         inv[i]=inv[i-1]*inv[i]%mod;
34 }
35 ll C(ll n,ll m)
36 {
37     return fac[n]*inv[m]%mod*inv[n-m]%mod;
38 }
39
40 int main()
41 {
42     ios::sync_with_stdio(false);
43     cin.tie(0);
44     cout.tie(0);
45     init();
46     ll n;
47     while(cin>>n){
48 /**打表找规律
49
50         ll p=0,q=1;
51         for(ll i=0;i<=n;i++){
52             a[i]=C(n,i);
53             b[i]=n-i+n+1;
54             a[i]%=mod;
55             b[i]%=mod;
56             if((n-i)&1) a[i]=-a[i];
57             q*=b[i];
58             q%=mod;
59             cout<<b[i]<<' ';
60         }
61         cout<<endl;
62         for(ll i=0;i<=n;i++){
63             p+=q*a[i]%mod*quick(b[i],mod-2);
64             p%=mod;
65         }
66         cout<<p<<endl;
67         ll x=__gcd(p,q);
68         p/=x,q/=x;
69         ll ans=(p*quick(q,mod-2))%mod;
70         cout<<ans<<endl;
71
72 **/
73         ll p=fac[n]*fac[n]%mod;
74         ll q=fac[2*n+1];
75         cout<<p*quick(q, mod-2)%mod<<endl;
76     }
77     return 0;
78 }