P1268 树的重量（板子）

题目：

题目描述

树可以用来表示物种之间的进化关系。一棵“进化树”是一个带边权的树，其叶节点表示一个物种，两个叶节点之间的距离表示两个物种的差异。现在，一个重要的问题是，根据物种之间的距离，重构相应的“进化树”。

令N={1..n}，用一个N上的矩阵M来定义树T。其中，矩阵M满足：对于任意的i，j，k，有M[i,j] + M[j,k] >= M[i,k]。树T满足：

1．叶节点属于集合N；

2．边权均为非负整数；

3．dT(i,j)=M[i,j]，其中dT(i,j)表示树上i到j的最短路径长度。

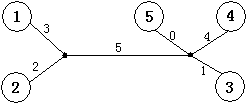
如下图，矩阵M描述了一棵树。

树的重量是指树上所有边权之和。对于任意给出的合法矩阵M，它所能表示树的重量是惟一确定的，不可能找到两棵不同重量的树，它们都符合矩阵M。你的任务就是，根据给出的矩阵M，计算M所表示树的重量。下图是上面给出的矩阵M所能表示的一棵树，这棵树的总重量为15。

输入格式

输入数据包含若干组数据。每组数据的第一行是一个整数n(2<n<30)。其后n-1行，给出的是矩阵M的一个上三角(不包含对角线)，矩阵中所有元素是不超过100的非负整数。输入数据保证合法。

输入数据以n=0结尾。

输出格式

对于每组输入，输出一行，一个整数，表示树的重量。

输入输出样例

输入 #1复制

5
5 9 12 8
8 11 7
5 1
4
4
15 36 60
31 55
36
0

输出 #1复制

15
71

题意：

就是给你一个n*n矩阵的右上部分，让你求出来树的重量

树的重量：树上所有边权之和。

给你一个n*n的矩阵，那么这个矩阵某个位置（i，j）的值dis(i,j)表示的就是i点和j点之间的距离

题解：

当n等于2的时候，那么树的重量就是dis(1,2)

当n大于2的时候：

从样例图（如下）中我们可以看到某些边是可以共用的

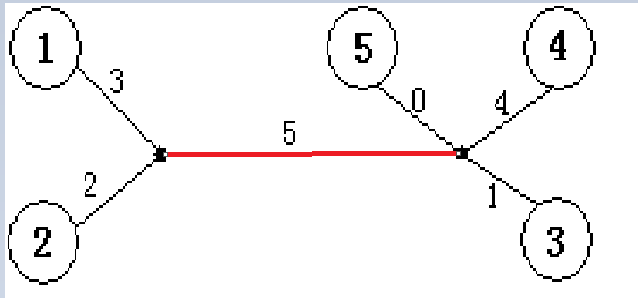
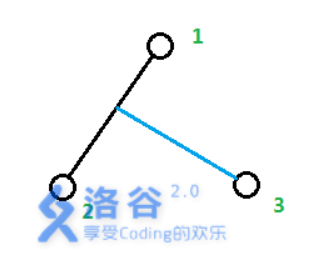
我们把上图的蓝色部分设为变量len

len= (dis(1,3)+dis(2,3)-dis(1,2))/2

公式泛化：

len=(dis(1,i)+dis(j,i)−dis(1,j))/2

我们只需要每次求出来最小的len就可以

for(int i=3;i<=n;++i)
        {
            int ans=INF;
            for(int j=2;j<i;++j)
            {
                ans=min(ans,(dis[1][i]+dis[j][i]-dis[1][j])/2);
            }
            sum+=ans;
        }

代码中的j为什么小于i？

看样例图，如果3，4，5点中的一个已经在代码中遍历过（比如5号点），那么其他点（3或4，这里用3做示范）就可以通过 (dis(1,3)+dis(5,3)-dis(1,5))/2=（9+1-8）/2=1

代码：

#include<stdio.h>
#include<string.h>
#include<iostream>
#include<algorithm>
using namespace std;
#define ll long long
#define mem(a) memset(a,0,sizeof(a))
const int maxn=30+10;
const int INF=0x3f3f3f3f;
int n,dis[maxn][maxn];
int main()
{
    while(~scanf("%d",&n))
    {
        if(!n) break;
        //mem(dis);  //不需要
        for(int i=1;i<n;++i)
        {
            for(int j=i+1;j<=n;++j)
            {
                scanf("%d",&dis[i][j]);
            }
        }
        int sum=dis[1][2];
        for(int i=3;i<=n;++i)
        {
            int ans=INF;
            for(int j=2;j<i;++j)
            {
                ans=min(ans,(dis[1][i]+dis[j][i]-dis[1][j])/2);
            }
            sum+=ans;
        }
        printf("%d\n",sum);
    }
    return 0;
}