Codeforces Round #496 (Div. 3) D. Polycarp and Div 3 (数论)

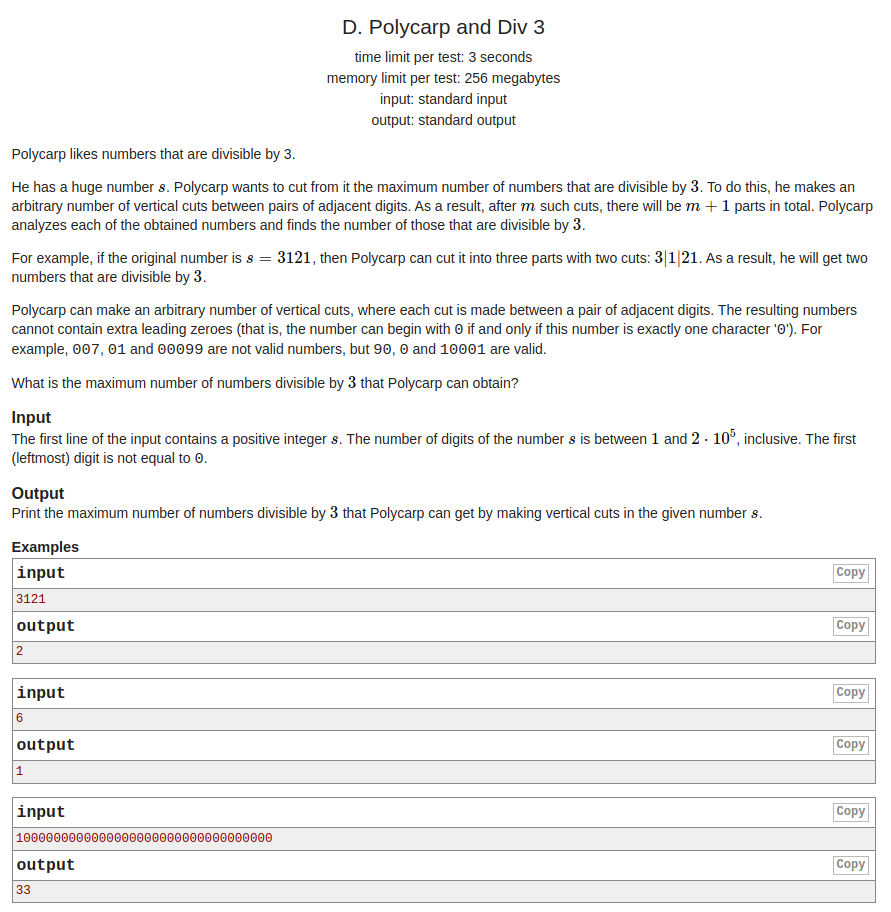
• 题意:给你一个巨长无比的数,你可以将这个数划成任意多个部分,求这些部分中最多有多少个能被\(3\)整除.

• 题解:首先我们遍历累加每个位置的数字,如果某一位数或者累加和能被\(3\)整除(基础知识,不会就去百度),那这就是一部分,再来,我们可以发现一个部分最长只有\(3\)个数字.

  证:当我这个部分有\(3\)个数字的时候,前两个数字\(mod\ 3\)的余数肯定同时为\(1\)或\(2\),这个时候:

  假如第三个数字\(mod\ 3=1\)且前两个数字\(mod\ 3 = 1\),那这个三个数加起来肯定被\(3\)整除(前面说过).

  假如第三个数字\(mod\ 3= 1\)且前两个数字\(mod\ 3=2\),那第二个和第三个数字的和被\(3\)整除.

  同理,当第三个数字\(mod\ 3 = 2\)的时候与上面一样.

  ​ 于是,我们只要判断长度为\(3\),某位数是否被整除,累积和是否被整除,这三种情况即可.

• 代码

  #include <iostream>
  #include <cstdio>
  #include <cstring>
  #include <cmath>
  #include <algorithm>
  #include <stack>
  #include <queue>
  #include <vector>
  #include <map>
  #include <set>
  #include <unordered_set>
  #include <unordered_map>
  #define ll long long
  #define fi first
  #define se second
  #define pb push_back
  #define me memset
  const int N = 1e6 + 10;
  const int mod = 1e9 + 7;
  const int INF = 0x3f3f3f3f;
  using namespace std;
  typedef pair<int,int> PII;
  typedef pair<ll,ll> PLL;
  string s;
  int cnt,res;
  int pre;
  int main() {
      ios::sync_with_stdio(false);cin.tie(0);
  	cin>>s;
  	 for(int i=0;i<s.size();++i){
  	 	pre+=s[i]-'0';
  	 	cnt++;
  	 	if(cnt==3 || (s[i]-'0')%3==0 || pre%3==0){
  	 		res++;
  	 		cnt=0;
  	 		pre=0;
  	 	}
  	 }
  	 printf("%d\n",res);
      return 0;
  }