BJOI2018 day2

双人猜数游戏

Alice 和 Bob 是一对非常聪明的人，他们可以算出各种各样游戏的最优策略。现在有个综艺节目《最强大佬》请他们来玩一个游戏。主持人写了三个正整数 \(s\) 、\(m\) 、\(n\) ，然后一起告诉 Alice 和 Bob \(s \leq m \leq n\) 以及 \(s\) 是多少。（即，\(s\) 是接 下来要猜的 \(m\) 、\(n\) 的下限。）之后主持人单独告诉 Alice \(m\) 与 \(n\) 的乘积是多少， 单独告诉 Bob \(m\) 与 \(n\) 的和是多少。

当然，如果一个人同时知道 \(m\) 与 \(n\) 的乘积以及 \(m\) 与 \(n\) 的和话就能很容易地算出 \(m\)和 \(n\) 分别是多少，但现在 Alice 和 Bob 只分别知道其中一个，而且只分别知道其中一个，而且他们只能回答主持人的问题，不能交流。从 Alice 或 Bob（见输入）开始 依次询问 Alice/Bob 知不知道 \(m\) 和 \(n\) 分别是多少， Alice/Bob 只能回答知道/不知道。

为了节目效果，为了显示出 Alice 和 Bob 非常聪明，主持人希望 Alice 和 Bob 一共说了 \(t\) 次“不知道 ”以后两个人都知道 \(m\) 和 \(n\) 是多少了 。现在主持人找到你，希望让帮他构造一组符合条件的 \(m\) 和 \(n\) 。

对于 \(40\%\) 的数据， \(t = 2\)；

对于 \(100\%\) 的数据， \(1 \leq s \leq 200\)，\(2 \leq t \leq 15\)，输入数据保证有解。

题解

模拟样例就大概知道他们搜索的过程。

考场上直接手动模拟，期望40分。

int calcA(int s,int m,int n){
	vector<pair<int,int> > solA;
	for(int i=s;i*i<=m*n;++i)if(m*n%i==0)
		solA.push_back(make_pair(i,m*n/i));
	if(solA.size()==1) return 0;

	vector<pair<int,int> > solB;
	for(int i=s;2*i<=m+n;++i)
		solB.push_back(make_pair(i,m+n-i));
	if(solB.size()==1) return 1;

	vector<vector<pair<int,int> > > solBsolA(solB.size());
	for(int i=0;i<(int)solB.size();++i){
		int a=solB[i].first,b=solB[i].second;
		for(int j=s;j*j<=a*b;++j)if(a*b%j==0)
			solBsolA[i].push_back(make_pair(j,a*b/j));
		if(solBsolA[i].size()==1){
			solB.erase(solB.begin()+i);
			solBsolA.erase(solBsolA.begin()+i);
			--i;
			continue;
		}
	}
	if(solBsolA.size()==1) return 1;

	vector<vector<vector<pair<int,int> > > > solAsolBsolA(solA.size());
	for(int i=0;i<(int)solA.size();++i){
		int a=solA[i].first,b=solA[i].second;
		for(int c=s;2*c<=a+b;++c){
			solAsolBsolA[i].push_back(vector<pair<int,int> >());
			int d=a+b-c;
			for(int j=s;j*j<=c*d;++j)if(c*d%j==0){
				solAsolBsolA[i].back().push_back(make_pair(j,c*d/j));
			}
			if(solAsolBsolA[i].back().size()==1){
				solAsolBsolA[i].erase(solAsolBsolA[i].begin()+solAsolBsolA[i].size());
			}
		}
		if(solAsolBsolA[i].size()==1){
			solA.erase(solA.begin()+i);
			solAsolBsolA.erase(solAsolBsolA.begin()+i);
			--i;
			continue;
		}
	}
	if(solAsolBsolA.size()==1) return 2;
	return 1000;
}

int calcB(int s,int m,int n){
	vector<pair<int,int> > solB;
	for(int i=s;2*i<=m+n;++i)
		solB.push_back(make_pair(i,m+n-i));
	if(solB.size()==1) return 0;

	vector<pair<int,int> > solA;
	for(int i=s;i*i<=m*n;++i)if(m*n%i==0)
		solA.push_back(make_pair(i,m*n/i));
	if(solA.size()==1) return 1;

	vector<vector<pair<int,int> > > solAsolB(solA.size());
	for(int i=0;i<(int)solA.size();++i){
		int a=solA[i].first,b=solA[i].second;
		for(int j=s;2*j<=a+b;++j)
			solAsolB[i].push_back(make_pair(j,a+b-j));
		if(solAsolB[i].size()==1){
			solA.erase(solA.begin()+i);
			solAsolB.erase(solAsolB.begin()+i);
			--i;
			continue;
		}
	}
	if(solAsolB.size()==1) return 1;

	vector<vector<vector<pair<int,int> > > > solBsolAsolB(solB.size());
	for(int i=0;i<(int)solB.size();++i){
		int a=solB[i].first,b=solB[i].second;
		for(int c=s;c*c<=a*b;++c)if(a*b%c==0){
			solBsolAsolB[i].push_back(vector<pair<int,int> > ());
			int d=a*b/c;
			for(int j=s;2*j<=c+d;++j)
				solBsolAsolB[i].back().push_back(make_pair(j,c+d-j));
			if(solBsolAsolB[i].back().size()==1){
				solBsolAsolB[i].erase(solBsolAsolB[i].begin()+solBsolAsolB[i].size());
			}
		}
		if(solBsolAsolB[i].size()==1){
			solB.erase(solB.begin()+i);
			solBsolAsolB.erase(solBsolAsolB.begin()+i);
			--i;
			continue;
		}
	}
	if(solBsolAsolB.size()==1) return 2;
	return 1000;
}

int main(){
	freopen("guess10.in","r",stdin),freopen("guess10.out","w",stdout);
	int s=read<int>();
	char name[10];scanf("%s",name);
	int t=read<int>();
	assert(t==2);
	if(name[0]=='A'){
		pair<int,int> ans=make_pair(1000,1000);
		for(int m=s;m<=400;++m)for(int n=m;n<=400;++n){
			if(n==m) cerr<<m<<" "<<n<<endl;
			if(calcA(s,m,n)==t){
				if(m+n<ans.first+ans.second or
				   (m+n==ans.first+ans.second and m<ans.first)) ans=make_pair(m,n);
			}
		}
		printf("%d %d\n",ans.first,ans.second);
	}
	else{
		pair<int,int> ans=make_pair(1000,1000);
		for(int m=s;m<=400;++m)for(int n=m;n<=400;++n){
			if(n==m) cerr<<m<<" "<<n<<endl;
			if(calcB(s,m,n)==t){
				if(m+n<ans.first+ans.second or
				   (m+n==ans.first+ans.second and m<ans.first)) ans=make_pair(m,n);
			}
		}
		printf("%d %d\n",ans.first,ans.second);
	}
	return 0;
}

实际得分28，因为我没有判断第一个人叫知道之后第二个人紧跟着也知道了。

手玩样例

这题看起来真是神仙，差不多就是两个神仙人不停地说不知道，然后突然就知道了。。。

所以我们要来手（解）玩（释）一下样例。

这里先不讲如何求答案，就来讲一下这答案为什么可以，以样例\(1\)为例。

最后得到的\(m,n\)分别为\(6,10\)，也就是说\(Alice\)和\(Bob\)分别得到的是\(60\)和\(16\)。

那我们来模拟一下他们的思路：

第1轮

• Bob：对于Bob来说，\(16=5+11=6+10=7+9=8+8\)，在没有任何信息的情况下，无法排除任何一种答案。

• Alice：对于Alice来说，\(60=5*12=6*10\)，这两种情况下的和分别为\(17\)和\(16\)，而如果Bob得到的是\(17\)或\(16\)，都不能一次确定答案，因此Alice也无法排除任何一种答案。

第2轮

• Bob：上面提到过的\(4\)种情况，所对应的积分别为\(55,60,63,64\)，而除了\(60\)以外，其余\(3\)种情况在\(5\le m\le n\)的情况下都只有一种分解方式，所以Alice可以直接确定。而\(Alice\)依然不知道，因此可以将这\(3\)种情况排除，就得出答案为\(6,10\)。

• Alice：同理，在Bob确定之后也可以通过类似的方式确定。

动态规划

我们可以考虑用动态规划+剪枝来做这题。

设\(f_{i,j,k}\)表示已经说过\(i\)次不知道，且两个数分别为\(j,k\)时是否能确定。

显然，对于每个人的询问是隔两次出现一次的。

而一个人如果上次被询问时已经知道答案了，下一次询问自然也知道。

于是可以推出第一个转移式：\(f_{i,j,k}=f_{i-2,j,k}\)。

而光这一个式子显然是不够的（废话），考虑上面手玩样例的过程，我们可以发现，以Alice为例，如果与\(j,k\)乘积相等的其他情况（设为\(x,y\)）都可以使\(f_{i-1,x,y}=1\)（即如果是这种情况，上一次询问时另一个人就能得出答案），且\(f_{i-1,j,k}=0\)，就可以排除其他所有情况，确定\(f_{i,j,k}=1\)。

对于Bob同理。

这样就可以通过动态规划来预处理出\(f\)数组了。

求出答案

考虑到题目首先要求\(m+n\)最小，其次要求\(m\)最小，因此考虑先枚举\(m+n\)，然后枚举\(m\)。

于是就变成了判断一对\(m,n\)是否符合题目要求。

首先，由于要恰好说\(t\)次不知道，因此我们要保证对于任一\(i<t\)，\(f_{i,m,n}=0\)。

然后，还要特判一下\(f_{t+1,m,n}\)是否确定，即判断此时的情况是否唯一，不然依然无法做到恰好说\(t\)次不知道。

这与之前动态规划的第二种转移方式的代码类似，具体实现详见代码。

CO int N=300+10;
int s;string name;int t;
bool f[N][N][20];

bool check_Alice(int x,int y,int t){
	bool flag=0;
	for(int i=s;i*i<=x*y;++i)if(x*y%i==0){
		int j=x*y/i;
		if(!t or !f[i][j][t-1]){
			if(i!=x) return 0;
			else flag=1;
		}
	}
	return flag;
}
bool check_Bob(int x,int y,int t){
	bool flag=0;
	for(int i=s;2*i<=x+y;++i){
		int j=x+y-i;
		if(!t or !f[i][j][t-1]){
			if(i!=x) return 0;
			else flag=1;
		}
	}
	return flag;
}
bool check_Alice_end(int x,int y){
	bool flag=0;
	for(int i=s;i*i<=x*y;++i)if(x*y%i==0){
		int j=x*y/i;
		if((t<2 or !f[i][j][t-2]) and f[i][j][t]){
			if(i!=x) return 0;
			else flag=1;
		}
	}
	return flag;
}
bool check_Bob_end(int x,int y){
	bool flag=0;
	for(int i=s;2*i<=x+y;++i){
		int j=x+y-i;
		if((t<2 or !f[i][j][t-2]) and f[i][j][t]){
			if(i!=x) return 0;
			else flag=1;
		}
	}
	return flag;
}

int main(){
	ios::sync_with_stdio(0);
	cin>>s>>name>>t;
	bool flag=name=="Alice";
	for(int k=0;k<=t;++k,flag^=1)
		for(int i=s;i<=300;++i)for(int j=i;j<=300;++j){
			if(k>=2) f[i][j][k]=f[i][j][k-2];
			if(!f[i][j][t]) f[i][j][k]=flag?check_Alice(i,j,k):check_Bob(i,j,k);
		}
	for(int sum=2*s;;++sum)for(int i=s;2*i<=sum;++i){
		int j=sum-i;
		if(!f[i][j][t]) continue;
		bool flag=1;
		for(int k=0;k<t;++k)
			if(f[i][j][k]) {flag=0;break;}
		if(!flag) continue;
		if((t&1)==(name=="Alice")?check_Alice_end(i,j):check_Bob_end(i,j)){
			cout<<i<<" "<<j<<endl;
			return 0;
		}
	}
	return 0;
}

链上二次求和

有一条长度为 \(n\) 的链（ \(\forall 1 \leq i < n\) ，点 \(i\) 与点 \(i+1\) 之间有一条边的无向图）， 每个点有一个整数权值，第 \(i\) 个点的权值是 \(a_i\) 。现在有 \(m\) 个操作，每个操作如下：

操作 1（修改）：给定链上两个节点 \(u\)、\(v\) 和一个整数 \(d\)，表示将链上 \(u\) 到 \(v\) 唯一的简单路径上每个点权值都加上 \(d\)。

操作 2（询问）：给定两个正整数 \(l\)、\(r\)，表示求链上所有节点个数大于等于 \(l\) 且小于等于 \(r\) 的简单路径节点权值和之和。由于答案很大，只用输出对质数 \(1000000007\) 取模的结果即可。

一条节点个数为 \(k\) 的简单路径节点权值和为这条上所有 \(k\) 个节点（包括端点）的权值之和，而本题中要求是对所有满足要求的简单路径，求这一权值和的和。

由于是无向图，路径也是无向的，即点 \(1\) 到点 \(2\) 的路径与点 \(2\) 到点 \(1\) 的路径是同一条，不要重复计算。

记操作 1（修改）的次数为 \(m^\prime\)。

对于全部数据， 保证 \(n \leq 200000, m \leq 500000, m^\prime \leq 100000, 0 \leq a_i < 1000000007\)

\(1 \leq u \leq n, 1\leq v \leq n, 0 \leq d < 1000000007, l \leq r \leq n\) 。

题解

考试的时候一看这个数据范围就知道这是个线段树题。

推公式，令 \(sa_i=\sum_{j=1}^ia_i\)，那么

\[ans_{len}=\sum_{i=len}^n(sa_i-sa_{i-len})
\]

令 \(ssa_i=\sum_{j=1}^isa_i\)，则

\[ans_{len}=ssa_n-ssa_{len-1}-ssa_{n-len}
\]

那么每次询问时

\[\sum_{i=l}^rans_i=(r-l+1)ssa_n-\sum_{i=l-1}^{r-1}ssa_i-\sum_{i=n-r}^{n-l}ssa_i
\]

那么我们只需要维护 \(ssa\) 即可。

考虑 \(a\) 的变化对 \(ssa\) 的影响。

\[ssa_i=\sum_{j=1}^i\sum_{k=1}^ja_k=\sum_{k=1}^i(i-k+1)a_k
\]

所以 \(a_k\) 对身后（\(i>k\)）的 \(ssa_i\) 有他们两者之间距离（\(i-k+1\)）的贡献。

对区间修改的贡献画个图如下：

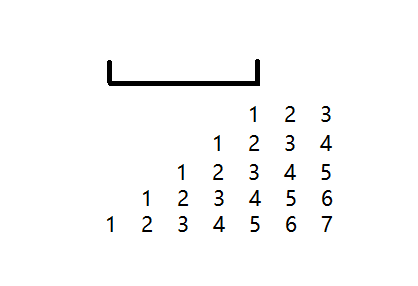
可以把这个贡献分为两段。

1. \(v\) 对 \([l,r]\) 内 \(i\) 的贡献是 \(\frac{(i-l+2)(i-l+1)}{2}v\)。
2. 记 \(len=r-l+1\)，那么 \(v\) 对 \([r+1,n]\) 内 \(i\) 的贡献是 \(\left(\frac{(len+1)len}{2}+(i-r)len\right)v\)。

由于我们只需要对 \(ssa\) 区间求和，所以在线段树上维护 \(i^0,i^1,i^2\) 的加法标记即可。

时间复杂度 \(O(m\log n)\)。

CO int mod=1000000000+7,i2=500000004;
IN int add(int a,int b){
	return (a+=b)>=mod?a-mod:a;
}
IN int mul(int a,int b){
	return (LL)a*b%mod;
}
IN int fpow(int a,int b){
	int ans=1;
	for(;b;b>>=1,a=mul(a,a))
		if(b&1) ans=mul(ans,a);
	return ans;
}

CO int N=200000+10;
int a[N],sa[N],ssa[N];

int sum[4*N],tag[4*N][3];

#define lc (x<<1)
#define rc (x<<1|1)
#define mid ((l+r)>>1)
IN void push_up(int x){
	sum[x]=add(sum[lc],sum[rc]);
}
void build(int x,int l,int r){
	fill(tag[x],tag[x]+3,0);
	if(l==r){
		sum[x]=ssa[l];
		return;
	}
	build(lc,l,mid),build(rc,mid+1,r);
	push_up(x);
}
IN int query(int d,int n){
	if(d==0) return n;
	else if(d==1) return (LL)n*(n+1)/2%mod;
	else return (LL)n*(n+1)*(2*n+1)/6%mod;
}
IN void push_down(int x,int l,int r){
	int chg=0;
	for(int d=0;d<=2;++d)if(tag[x][d]){
		sum[lc]=add(sum[lc],mul(add(query(d,mid),mod-query(d,l-1)),tag[x][d]));
		tag[lc][d]=add(tag[lc][d],tag[x][d]);
		sum[rc]=add(sum[rc],mul(add(query(d,r),mod-query(d,mid)),tag[x][d]));
		chg=add(chg,mul(add(query(d,r),mod-query(d,mid)),tag[x][d]));
		tag[rc][d]=add(tag[rc][d],tag[x][d]);
		tag[x][d]=0;
	}
}
void change(int x,int l,int r,int ql,int qr,int v[3]){
	if(ql<=l and r<=qr){
		for(int d=0;d<=2;++d){
			sum[x]=add(sum[x],mul(add(query(d,r),mod-query(d,l-1)),v[d]));
			tag[x][d]=add(tag[x][d],v[d]);
		}
		return;
	}
	push_down(x,l,r);
	if(ql<=mid) change(lc,l,mid,ql,qr,v);
	if(qr>mid) change(rc,mid+1,r,ql,qr,v);
	push_up(x);
}
int query(int x,int l,int r,int ql,int qr){
	if(ql<=l and r<=qr) return sum[x];
	push_down(x,l,r);
	if(qr<=mid) return query(lc,l,mid,ql,qr);
	if(ql>mid) return query(rc,mid+1,r,ql,qr);
	return add(query(lc,l,mid,ql,qr),query(rc,mid+1,r,ql,qr));
}

int main(){
//	freopen("sum.in","r",stdin),freopen("sum.out","w",stdout);
	int n=read<int>(),m=read<int>();
	for(int i=1;i<=n;++i){
		read(a[i]);
		sa[i]=add(sa[i-1],a[i]);
		ssa[i]=add(ssa[i-1],sa[i]);
	}
	build(1,1,n);
	while(m--){
		if(read<int>()==1){
			int l=read<int>(),r=read<int>(),v=read<int>();
			if(l>r) swap(l,r);
			int tlr[3];
			tlr[0]=mul((LL)(l-2)*(l-1)/2%mod,v);
			tlr[1]=mul(add(3,mod-2*l),mul(i2,v));
			tlr[2]=mul(i2,v);
			change(1,1,n,l,r,tlr);
			if(r+1<=n){
				int len=r-l+1,trn[3];
				trn[0]=mul(add((LL)(len+1)*len/2%mod,mod-mul(len,r)),v);
				trn[1]=mul(len,v);
				trn[2]=0;
				change(1,1,n,r+1,n,trn);
			}
		}
		else{
			int l=read<int>(),r=read<int>();
			int ans=mul(r-l+1,query(1,1,n,n,n));
			if(r-1>=1) ans=add(ans,mod-query(1,1,n,max(l-1,1),r-1));
			if(n-l>=1) ans=add(ans,mod-query(1,1,n,max(n-r,1),n-l));
			printf("%d\n",ans);
		}
	}
	return 0;
}

另外值得注意的是，输入中给的是 \(u,v\) 之间的唯一路径，那么可能 \(u>v\)。估计有很多人FST。

治疗之雨

（没玩过《炉石传说》的人可以跳过这一段）今天我们来探讨下《炉石传说》中“治疗之雨”（恢复 \(12\) 点生命值，随机分配到所有友方角色上）和“暗影打击装甲”（每当一个角色获得治疗，便对随机敌人造成 \(1\) 点伤害）这两张卡牌之间的互动效果。假设你场上有 \(m\) 个剩余生命值无限大且生命值上限减去剩余生命值也无限大的随从，而对方的场上有 \(k\) 个暗影打击装甲，你的英雄剩余生命值为 \(p\) 、生命值上限为 \(n\) ，现在你使用了一张可以恢复无限多（而不是 \(12\) 点）生命值的治疗之雨，问治疗之雨期望总共恢复了几点生命值以后你的英雄会死亡（生命值降为 \(0\) ；治疗之雨的判定机制使得在此后再也不会为英雄恢复生命值）。

注：题目背景与题目描述有冲突的地方请以题目描述为准

下面让我们再形式化地描述一遍问题。

你现在有 \(m+1\) 个数：第一个为 \(p\) ，最小值为 \(0\) ，最大值为 \(n\) ；剩下 \(m\) 个都是无穷，没有最小值或最大值。你可以进行任意多轮操作，每轮操作如下：

在不为最大值的数中等概率随机选择一个（如果没有则不操作），把它加一；

进行 \(k\) 次这个步骤：在不为最小值的数中等概率随机选择一个（如果没有则不操作），把它减一。

现在问期望进行多少轮操作以后第一个数会变为最小值 \(0\) 。

对于 \(100\%\) 的数据， \(1 \leq T \leq 100\)，\(1 \leq p \leq n \leq 1500\) ，\(0 \leq m, k \leq 1000000000\)。

//保证不存在 \(n=p=k=1\) ， \(m=0\) 的情况（因为出题人判错了）

//保证不存在答案的分母是\(1000000007\)的倍数的情况（因为出题人没想到）

题解

这题最重要的就是搞懂题意。

然后DP状态十分简单，\(E(i)\) 表示还有 \(i\) 滴血时的期望。

转移系数是二项分布。

但是高斯消元复杂度炸了，需要特殊处理。

注意到矩阵系数不为0的格子的形式：

1	1	0	0	0	0
1	1	1	0	0	0
1	1	1	1	0	0
1	1	1	1	1	0
1	1	1	1	1	1
1	1	1	1	1	1

所以每行只会两格两格地消，时间复杂度 \(O(n^2)\)。

CO int N=1500+10;
int inv[N],prob[N];
int a[N][N];

void real_main(){
	int n=read<int>(),p=read<int>(),m=read<int>(),k=read<int>();
	if(k==0) return puts("-1"),void();
	if(m==0){
		if(k==1){
			if(n>1) return puts("-1"),void();
			else return puts("1"),void();
		}
		int cnt=1;
		p=p<n?p+1-k:p-k;
		if(p>0) cnt+=(p+k-2)/(k-1);
		printf("%d\n",cnt);
		return;
	}
	int p0=fpow(m+1,mod-2),p1=add(1,mod-p0);
	prob[0]=fpow(p1,k);
	for(int ip1=fpow(p1,mod-2),i=1;i<=n;++i){
		prob[i]=mul(prob[i-1],mul(k-i+1,inv[i]));
		prob[i]=mul(prob[i],mul(p0,ip1));
	}
	memset(a,0,sizeof a);
	for(int i=1;i<n;++i){
		a[i][i+1]=mod-mul(p0,prob[0]);
		for(int j=0;j<min(i,k);++j)
			a[i][i-j]=mod-add(mul(p0,prob[j+1]),mul(p1,prob[j]));
		if(k<i) a[i][i-k]=mod-mul(p1,prob[k]);
		a[i][i]=add(a[i][i],1),a[i][n+1]=1;
	}
	for(int i=0;i<=min(n-1,k);++i)
		a[n][n-i]=mod-prob[i];
	a[n][n]=add(a[n][n],1),a[n][n+1]=1;
	for(int i=1;i<n;++i){
		int inv=fpow(a[i][i],mod-2);
		for(int j=i+1;j<=n;++j){
			int alph=mul(mod-a[j][i],inv);
			a[j][i]=add(a[j][i],mul(alph,a[i][i]));
			a[j][i+1]=add(a[j][i+1],mul(alph,a[i][i+1]));
			a[j][n+1]=add(a[j][n+1],mul(alph,a[i][n+1]));
		}
	}
	a[n][n+1]=mul(a[n][n+1],fpow(a[n][n],mod-2)),a[n][n]=1;
	for(int i=n-1;i>=1;--i){
		a[i][n+1]=add(a[i][n+1],mod-mul(a[i][i+1],a[i+1][n+1])),a[i][i+1]=0;
		a[i][n+1]=mul(a[i][n+1],fpow(a[i][i],mod-2)),a[i][i]=1;
	}
	printf("%d\n",a[p][n+1]);
}
int main(){
	inv[0]=inv[1]=1;
	for(int i=2;i<N;++i) inv[i]=mul(mod-mod/i,inv[mod%i]);
	for(int T=read<int>();T--;) real_main();
	return 0;
}