jdk7中hashmap实现原理和jdk8中hashmap的改进方法总结

1. HashMap的数据结构

数据结构中有数组和链表来实现对数据的存储，但这两者基本上是两个极端。

数组

数组存储区间是连续的，占用内存严重，故空间复杂的很大。但数组的二分查找时间复杂度小，为O(1)；数组的特点是：寻址容易，插入和删除困难；

链表

链表存储区间离散，占用内存比较宽松，故空间复杂度很小，但时间复杂度很大，达O（N）。链表的特点是：寻址困难，插入和删除容易。

哈希表

那么我们能不能综合两者的特性，做出一种寻址容易，插入删除也容易的数据结构？答案是肯定的，这就是我们要提起的哈希表。哈希表（(Hash table）既满足了数据的查找方便，同时不占用太多的内容空间，使用也十分方便。

　　哈希表有多种不同的实现方法，我接下来解释的是最常用的一种方法—— 拉链法，我们可以理解为“链表的数组” ，如图：

 

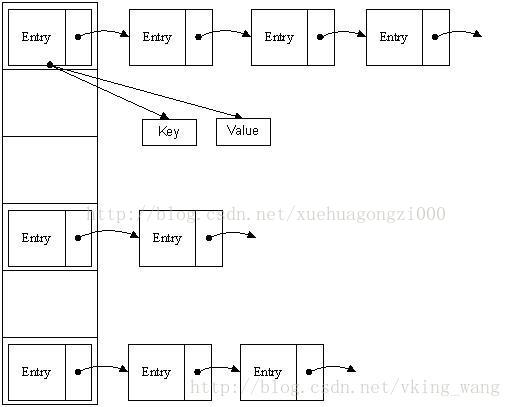
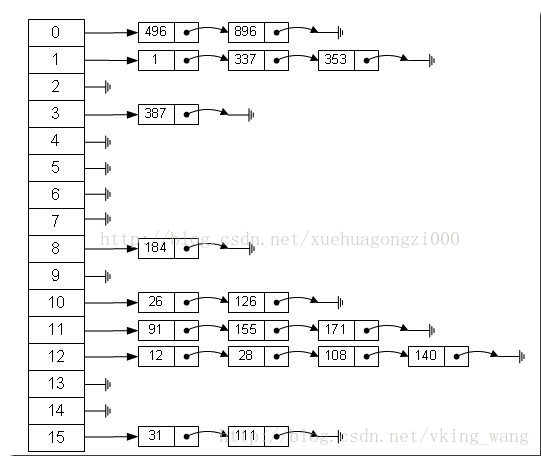
从上图我们可以发现哈希表是由数组+链表组成的，一个长度为16的数组中，每个元素存储的是一个链表的头结点。那么这些元素是按照什么样的规则存储到数组中呢。一般情况是通过hash(key)%len获得，也就是元素的key的哈希值对数组长度取模得到。比如上述哈希表中，12%16=12,28%16=12,108%16=12,140%16=12。所以12、28、108以及140都存储在数组下标为12的位置。

　　HashMap其实也是一个线性的数组实现的,所以可以理解为其存储数据的容器就是一个线性数组。这可能让我们很不解，一个线性的数组怎么实现按键值对来存取数据呢？这里HashMap有做一些处理。

　　首先HashMap里面实现一个静态内部类Entry，其重要的属性有 key , value, next，从属性key,value我们就能很明显的看出来Entry就是HashMap键值对实现的一个基础bean，我们上面说到HashMap的基础就是一个线性数组，这个数组就是Entry[]，Map里面的内容都保存在Entry[]里面。

   /**
     * The table, resized as necessary. Length MUST Always be a power of two.
     */
    transient Entry[] table;

2. HashMap的存取实现

既然是线性数组，为什么能随机存取？这里HashMap用了一个小算法，大致是这样实现：

// 存储时:
int hash = key.hashCode(); // 这个hashCode方法这里不详述,只要理解每个key的hash是一个固定的int值
int index = hash % Entry[].length;
Entry[index] = value;

// 取值时:
int hash = key.hashCode();
int index = hash % Entry[].length;
return Entry[index];

 

1）put

 

疑问：如果两个key通过hash%Entry[].length得到的index相同，会不会有覆盖的危险？

　　这里HashMap里面用到链式数据结构的一个概念。上面我们提到过Entry类里面有一个next属性，作用是指向下一个Entry。打个比方， 第一个键值对A进来，通过计算其key的hash得到的index=0，记做:Entry[0] = A。一会后又进来一个键值对B，通过计算其index也等于0，现在怎么办？HashMap会这样做:B.next = A,Entry[0] = B,如果又进来C,index也等于0,那么C.next = B,Entry[0] = C；这样我们发现index=0的地方其实存取了A,B,C三个键值对,他们通过next这个属性链接在一起。所以疑问不用担心。也就是说数组中存储的是最后插入的元素（在前面进行插入）。到这里为止，HashMap的大致实现，我们应该已经清楚了。

 public V put(K key, V value) {
         if (key == null)
             return putForNullKey(value); //null总是放在数组的第一个链表中
         int hash = hash(key.hashCode());
         int i = indexFor(hash, table.length);
         //遍历链表
         for (Entry<K,V> e = table[i]; e != null; e = e.next) {
             Object k;
             //如果key在链表中已存在，则替换为新value
             if (e.hash == hash && ((k = e.key) == key || key.equals(k))) {
                 V oldValue = e.value;
                 e.value = value;
                 e.recordAccess(this);
                 return oldValue;
             }
         }

         modCount++;
         addEntry(hash, key, value, i);
         return null;
     }

 void addEntry(int hash, K key, V value, int bucketIndex) {
     Entry<K,V> e = table[bucketIndex];
     table[bucketIndex] = new Entry<K,V>(hash, key, value, e); //参数e, 是Entry.next
     //如果size超过threshold，则扩充table大小。再散列
     if (size++ >= threshold)
             resize(2 * table.length);
 }

　　当然HashMap里面也包含一些优化方面的实现，这里也说一下。比如：Entry[]的长度一定后，随着map里面数据的越来越长，这样同一个index的链就会很长，会不会影响性能？HashMap里面设置一个因子，随着map的size越来越大，Entry[]会以一定的规则加长长度。

2）get

 public V get(Object key) {
         if (key == null)
             return getForNullKey();
         int hash = hash(key.hashCode());
         //先定位到数组元素，再遍历该元素处的链表
         for (Entry<K,V> e = table[indexFor(hash, table.length)];
              e != null;
              e = e.next) {
             Object k;
             if (e.hash == hash && ((k = e.key) == key || key.equals(k)))
                 return e.value;
         }
         return null;
 }

3）null key的存取

null key总是存放在Entry[]数组的第一个元素。

  private V putForNullKey(V value) {
         for (Entry<K,V> e = table[0]; e != null; e = e.next) {
             if (e.key == null) {
                 V oldValue = e.value;
                 e.value = value;
                 e.recordAccess(this);
                 return oldValue;
             }
         }
         modCount++;
         addEntry(0, null, value, 0);
         return null;
     }

     private V getForNullKey() {
         for (Entry<K,V> e = table[0]; e != null; e = e.next) {
             if (e.key == null)
                 return e.value;
         }
         return null;
     }

 

 

 

 

4）确定数组index：hashcode % table.length取模

HashMap存取时，都需要计算当前key应该对应Entry[]数组哪个元素，即计算数组下标；算法如下：

 /**
     * Returns index for hash code h.
     */
    static int indexFor(int h, int length) {
        return h & (length-1);
    }

 

按位取并，作用上相当于取模mod或者取余%。

这意味着数组下标相同，并不表示hashCode相同。

 

5）table初始大小

 

  public HashMap(int initialCapacity, float loadFactor) {
         .....

         // Find a power of 2 >= initialCapacity
         int capacity = 1;
         while (capacity < initialCapacity)
             capacity <<= 1;

         this.loadFactor = loadFactor;
         threshold = (int)(capacity * loadFactor);
         table = new Entry[capacity];
         init();
     }

 

注意table初始大小并不是构造函数中的initialCapacity！！

而是 >= initialCapacity的2的n次幂！！！！因为里面有移位操作，这样初始化更方便

3. 解决hash冲突的办法

1. 开放定址法（线性探测再散列，二次探测再散列，伪随机探测再散列）
2. 再哈希法
3. 链地址法
4. 建立一个公共溢出区

Java中hashmap的解决办法就是采用的链地址法。

4. 再散列resize/rehash过程

当哈希表的容量超过默认容量时，必须调整table的大小。当容量已经达到最大可能值时，那么该方法就将容量调整到Integer.MAX_VALUE返回，这时，需要创建一张新表，将原表的映射到新表中。

扩容的过程：

    /**
      * Rehashes the contents of this map into a new array with a
      * larger capacity.  This method is called automatically when the
      * number of keys in this map reaches its threshold.
      *
      * If current capacity is MAXIMUM_CAPACITY, this method does not
      * resize the map, but sets threshold to Integer.MAX_VALUE.
      * This has the effect of preventing future calls.
      *
      * @param newCapacity the new capacity, MUST be a power of two;
      *        must be greater than current capacity unless current
      *        capacity is MAXIMUM_CAPACITY (in which case value
      *        is irrelevant).
      */
     void resize(int newCapacity) {
         Entry[] oldTable = table;
         int oldCapacity = oldTable.length;
         if (oldCapacity == MAXIMUM_CAPACITY) {
             threshold = Integer.MAX_VALUE;
             return;
         }

         Entry[] newTable = new Entry[newCapacity];  //初始化一个新的Entry数组
         transfer(newTable);                  //！！将数据转移到新的Entry数组里
         table = newTable;               //HashMap的table属性引用新的Entry数组
         threshold = (int)(newCapacity * loadFactor);             //修改阈值
     }

     /**
      * Transfers all entries from current table to newTable.
      */
     void transfer(Entry[] newTable) {
         Entry[] src = table;
         int newCapacity = newTable.length;
         for (int j = 0; j < src.length; j++) {
             Entry<K,V> e = src[j];
             if (e != null) {
                 src[j] = null;
                 do {
                     Entry<K,V> next = e.next;
                     //重新计算index
                     int i = indexFor(e.hash, newCapacity);
                     e.next = newTable[i];
                     newTable[i] = e;
                     e = next;
                 } while (e != null);
             }
         }
     }

5.java8的性能改善

这里存在一个问题，即使负载因子和Hash算法设计的再合理，也免不了会出现拉链过长的情况，一旦出现拉链过长，则会严重影响HashMap的性能。于是，在JDK1.8版本中，对数据结构做了进一步的优化，引入了红黑树。而当链表长度太长（默认超过8）时，链表就转换为红黑树，利用红黑树快速增删改查的特点提高HashMap的性能，其中会用到红黑树的插入、删除、查找等算法。

当插入新元素时，对于红黑树的判断如下：

判断table[i] 是否为treeNode，即table[i] 是否是红黑树，如果是红黑树，则直接在树中插入键值对，否则转向下面；

遍历table[i]，判断链表长度是否大于8，大于8的话把链表转换为红黑树，在红黑树中执行插入操作，否则进行链表的插入操作；遍历过程中若发现key已经存在直接覆盖value即可；