Mesh网格简化

Mesh简化算法：

1. 通过mesh简化，可以将一个多边形的网格A转化成另一个网格B

网格B相比A，有更少的三角形面、边、顶点。

2. 简化的过程是受到一定的约束的。会有一系列自定义的质量标准来控制简化的进行。这些质量标准是为了让简化后的网格尽可能和原来的网格有相差不大的质量。

3. Mesh简化往往都是迭代的，例如每一次移除一个顶点或者一条边。并且这一过程是可以反转的，也就是可以通过优化后的网格，恢复到原网格

主要的简化算法：

1. 顶点聚集（Vertex Clustering）。

按照我自己的理解大致概述下，就是将距离 （记作ε ）一定范围内的顶点合并成一个代表顶点。

这种处理方式速度快，时间复杂度是O(n)，n是顶点数量。（暂留疑问为什么是O(n)）

当然缺陷也很明显，可能会出现一个三角形退化成一条线段甚至一个顶点的情况。

a) 聚集生成（Cluster Generation）

用一个大的方框囊括mesh，然后将这个大方框分割成一个个小空间（cells），确定一个数值 ε > 0，作为小空间的边长。然后将mesh映射到这个方框里

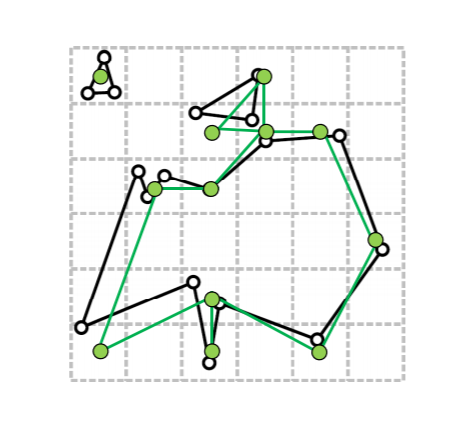
（上图白点黑线是原mesh，绿点是简化后的mesh顶点）

b) 选择代表顶点（Representative Vertex）

就是将一个小空间里的所有顶点合并，选一个代表顶点来表示（这个代表顶点不一定是原mesh中存在的顶点）

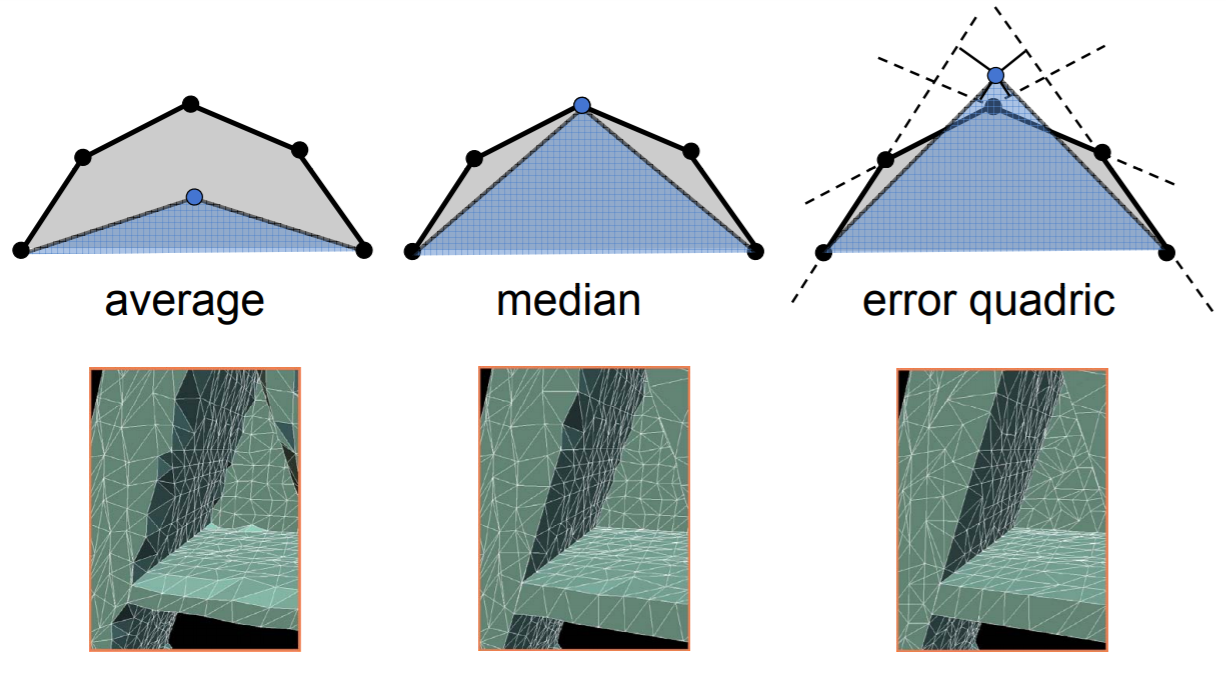
第一种选择方法：平均值

应该是将小空间内顶点坐标取平均，最后选取一个代表点v_p

第二种方法：中值

应该就是取最靠近中间的顶点吧

第三种方法：Quadrics Error Metrics(QEM) 二次误差测算

具体QEM的处理方式在另一篇文章中记录，其中我也有很多疑惑的地方，但还是简单的梳理了一遍

“QEM是一种误差度量，表示一个顶点到理想点的距离”，

按照我的理解就是，在一个小的空格（前面提到的cell）里，有多个顶点存在（共n个，v₁~v_n），最终我们需要选择一个代表点v_{p ，}

对于每个顶点，都计算一次用v_p代替v_i的二次误差；最后再将这n个二次误差加和E_sum。而我们的任务就是找到一个合适的点V_p，使得E_sum最小。

上述三种方法的效果如下：

c）网格生成（Mesh Generation）

经过上面步骤的处理，每个小空间（cell）中都会最多有一个代表点v_p

假设有两个cell，记作Cell_a和Cell_b，其代表点为v_pa，v_pb；

Cell_a中的顶点集合为{p₁,p₂, ..., p_n}，Cell_b中的顶点集合是{q₁,q₂, ..., q_m}，如果存在连线<p_i, q_j>，就将v_pa，v_pb连接

d）拓扑结构改变（Topology Changes）

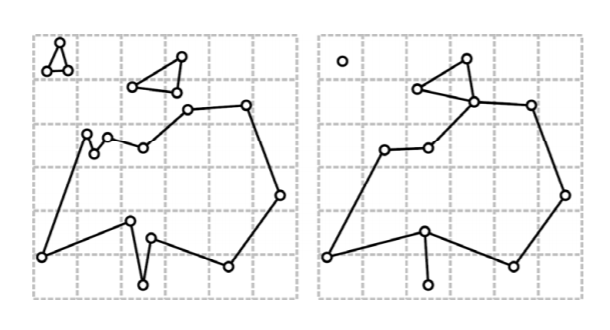
（这张图就可以看出上面提到的缺陷）

2. 增量式减少（Incremental Decimation）

a) 思路如下：

• Repeat:
• pick mesh region
• apply decimation operator
• Until no further reduction possible

针对一个网格区域，找到所有简化的方法（每种简化方法后都会生成一个新的网格区域）

然后（有错误评估值的控制，偏差超出范围的简化方案不做考虑）：

• For each region
• evaluate quality after decimation
• enqueue(quality, region)
• Repeat:
• get best mesh region from queue
• if error < ε
• apply decimation operator
• update queue
• Until no further reduction possible

对每个简化后的网格区域进行偏差评估，然后放入一个队列；

取出最优项（未完成）

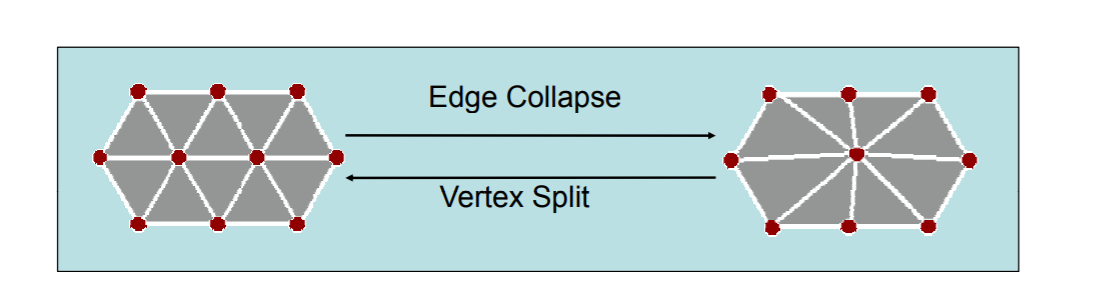
b) 简化处理方法（Decimation Operators）

包括顶点移除（Vertex Removal）、边去除（Edge Collapse）、Half-Edge Collapse（不知道怎么翻译了）

这几种处理方法看图解很清晰，不加赘述

c) 误差度量（Error Metrics）

分为局部误差度量和全局误差度量

局部误差度量，按我理解的是，对 简化处理导致平面减少 这一情况进行度量

全局误差度量，计算简化处理后的网格区域误差值（未完成）

d) Fairness Criteria （按照我的理解，指的是简化过程中需要注意的约束标准，一下几点具体解释都是我自己的推测）

合理的误差——简化处理导致的误差不能过大（似乎有点像废话）

三角面的形状——三角面的形状变化不能过大

3. 两种方法的比较

Vertex Clustering

a) 顶点聚集时间复杂度O(n)，处理速度快；但是简化过程难以控制（暂留疑问）

b) 拓扑结构（可能）会改变，（可能）会出现非流行网格

Increment Decimation

a) 在网格质量和简化速度之间有很好的平衡（暂留疑问）

b) 对网格的拓扑结构有明确的控制

c) 限制法向量偏差提升了网格质量

4. 参考

http://graphics.stanford.edu/courses/cs468-10-fall/LectureSlides/08_Simplification.pdf

https://pages.mtu.edu/~shene/COURSES/cs3621/SLIDES/Simplification.pdf