算法学习day01 栈和队列

1,设计一个算法利用顺序栈的基本运算判断一个字符串是否是回文
解题思路：
      由于回文是从前到后和从后到前读都是一样的，所以只要将待判断的字符串颠倒
然后与原字符串相比较，就可以决定是否是回文了

#include<stdio.h>
#include<stdlib.h>
#define MaxSize 100  //顺序栈的初始分配大小
typedef struct SqStack {
    char data[MaxSize];//保存栈中元素
    int top;//栈中指针
}SqStack;

//声明初始化方法
void initStack(SqStack &st);
//声明压栈方法
int Push(SqStack &st, char x);
//声明出栈方法
int Pop(SqStack &st, char &x);
//判断是否为空
int StackEmpty(SqStack st);
//声明判断是否是回文的方法
int isPalindrome(char str[]);
int main() {
    char str[] = "abcdcba";
    printf("是否是回文？1(是):0(不是)= %d \n", isPalindrome(str));
    return ;
}
//实现方法
//初始化
void initStack(SqStack &st) {//st为引用型参数
    st.top = -;
}
//压栈
int Push(SqStack &st, char x) {
    if (st.top==MaxSize-) {//栈满，上溢出，返回0
        return ;
    }
    else {
        st.top++;
        st.data[st.top] = x;
        return ;//成功进栈返回1
    }
}
//出栈
int Pop(SqStack &st, char &x) { //x为引用型参数
    if (st.top == -) {
        return ;
    }
    else {
        x = st.data[st.top];
        st.top--;
        return ;//成功出栈返回1
    }
}

//判断是否为空
int StackEmpty(SqStack st) {
        if (st.top == -)return ;
        else return ;
}

//判定一个给定字符串str是否是回文，是返回1 不是返回0
int isPalindrome(char str[]) {
    SqStack st;//定义一个顺序栈st
    initStack(st);//栈初始化
    int i = ;
    char ch;
    while ((ch=str[i++])!='\0') //所有字符串一次进栈
        Push(st,ch);
        i = ;//从头开始遍历str

        while (!StackEmpty(st)) {
            Pop(st,ch);
            if (ch!=str[i++]) {//两字符不相同时返回0
                 //销毁栈返回0
                return ;
            }
        }
    return ;//所有字符都相同返回1
}

例2：设计一个算法，判断一个可能包含有小括号（“（”，“）”），中括号（“[”，“]”），大括号（“{”，“}”）的表达式中各类括号是否匹配，若匹配返回1，不匹配返回0
     解题思路：

设置一个栈st(使用字符数组存放栈中元素，再用一个整型变量top 作为栈顶指针)用i扫描表达式，忽略非括号字符，当遇到左括号“（”，”[","{",时，将其入栈，
遇到 } ] )时，判断栈顶是否相匹配的括号，若不是退出扫描，返回0，负责扫描完毕，若栈空则返回1，否则返回0；

#include <stdio.h>
#define MaxSize 100
int match(char *exps)                    //exps存放表达式
{    char st[MaxSize];
    int nomatch=,top=-,i=;
    while (exps[i]!='\0' && nomatch==)//遍历表达式exps
    {    switch(exps[i])
        {
        case '(': case '[': case '{':    //左括号进栈
            top++;st[top]=exps[i];break;
        case ')':                        //判断栈顶是否为'('
            if (st[top]=='(') top--;
            else nomatch=;
            break;
        case ']':                        //判断栈顶是否为'['
            if (st[top]=='[') top--;
            else nomatch=;
            break;
        case '}':                        //判断栈顶是否为'{'
            if (st[top]=='{') top--;
            else nomatch=;
            break;
        default:                        //跳过其他字符
            break;
        }
        i++;
    }
    if (nomatch== && top==-)        //栈空且符号匹配则返回1
        return ;
    else
        return ;                    //否则返回0
}
void main()
{
    char str1[]="[(])";
    char str2[]="[()]";
    char str3[]="[()])";
    char str4[]="([()]";
    printf("判断结果如下:\n");
    if (match(str1))
        printf("  %s是匹配的表达式\n",str1);
    else
        printf("  %s不是匹配的表达式\n",str1);
    if (match(str2))
        printf("  %s是匹配的表达式\n",str2);
    else
        printf("  %s不是匹配的表达式\n",str2);
    if (match(str3))
        printf("  %s是匹配的表达式\n",str3);
    else
        printf("  %s不是匹配的表达式\n",str3);
    if (match(str4))
        printf("  %s是匹配的表达式\n",str4);
    else
        printf("  %s不是匹配的表达式\n",str4);

}

例3：设计一个算法，将一个十进制正整数转换为相应的二进制数；

解题思路：

将十进制数转化为2进制数，通常才用除2取余法，在转换过程中，二进制数是从低位到高位的次序得到的，这和通常的从高位到低位输出相反，

为此设计一个栈，用于暂时存放每次得到的余数，当转换过程结束时，退栈所有元素便得到从高位到低位的二进制数，如下演示：

实现：

#include <stdio.h>
#define MaxSize 100
void trans(int d, char b[]) //b用于存放d转换成的二进制数的字符串
{
    char st[MaxSize], ch;
    int i = , top = -;        //栈顶指针top初始为-1
    while (d != )
    {
        ch = '' + d % ;     //求余数并转换为字符
        top++; st[top] = ch;    //字符ch进栈
        d /= ;               //继续求更高位
    }
    while (top != -)
    {
        b[i] = st[top];
        top--;            //出栈并存放在数组b中
        i++;
    }
    b[i] = '\0';                //加入字符串结束标志
}

void main()
{
    int d;
    char str[MaxSize];
    do
    {
        printf("输入一个正整数:");
        scanf("%d", &d);
    } while (d<);
    trans(d, str);
    printf("对应的二进制数:%s\n", str);

}

在较复杂的数据处理中，通常需要保存多个需要临时产生的数据，如果先产生的数据先处理，那么需要用队列来处理这些数据；

综合：设计一个算法，反映病人到医院看病，排队看医生的过程：

描述：病人排队看医生，采用先到先看的方式，所以要用到队列，由于病人人数具有较大的不确定性，这里采用一个带头结点的单链表作为队列的存储结构，为了简单，

病人通过其姓名来唯一标识，如下病人队列：

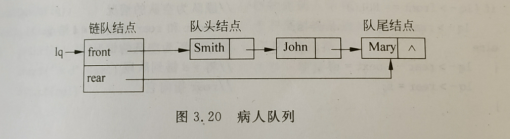
实现如下：

#include <stdio.h>
#include <malloc.h>
#include <string.h>
typedef struct Lnode
{    char data[];            //存放患者姓名
    struct Lnode *next;        //指针域
} QType;                    //链队结点类型
typedef struct
{    QType *front;            //指向队头病人结点
    QType *rear;            //指向队尾病人结点
} LQueue;                    //病人链队类型
//---初始化队列运算算法---
void InitQueue(LQueue *&lq)
{    lq=(LQueue *)malloc(sizeof(LQueue));
    lq->rear=lq->front=NULL;        //初始时队头和队尾指针均为空
}
//----销毁链队----
void DestroyQueue(LQueue *&lq)
{    QType *pre=lq->front,*p;
    if (pre!=NULL)                    //非空队的情况
    {    if (pre==lq->rear)            //只有一个数据结点的情况
            free(pre);                //释放*pre结点
        else                        //有两个或多个数据结点的情况
        {    p=pre->next;
            while (p!=NULL)
            {    free(pre);            //释放*pre结点
                pre=p; p=p->next;    //pre、p同步后移
            }
            free(pre);                //释放尾结点
        }
        free(lq);                    //释放链队结点
    }
}
//----进队运算算法----
void EnQueue(LQueue *&lq,char x[])
{    QType *s;
    s=(QType *)malloc(sizeof(QType));    //创建新结点，插入到链队的末尾
    strcpy(s->data,x);s->next=NULL;
    if (lq->front==NULL)                //原队为空队的情况
        lq->rear=lq->front=s;            //front和rear均指向*s结点
    else                                //原队不为空队的情况
    {    lq->rear->next=s;                //将*s链到队尾
        lq->rear=s;                        //rear指向它
    }
}
//-----出队运算算法-----
int DeQueue(LQueue *&lq,char x[])
{    QType *p;
    if (lq->front==NULL)        //原队为空队的情况
        return ;
    p=lq->front;                //p指向队头结点
    strcpy(x,p->data);            //取队头元素值
    if (lq->rear==lq->front)    //若原队列中只有一个结点,删除后队列变空
        lq->rear=lq->front=NULL;
    else                        //原队有两个或以上结点的情况
        lq->front=lq->front->next;
    free(p);
    return ;
}
//----判断队空运算算法----
int QueueEmpty(LQueue *lq)
{    if (lq->front==NULL) return ;    //队空返回1
    else return ;                    //队不空返回0
}
//----输出队中所有元素的算法----
int DispQueue(LQueue *lq)
{    QType *p;
    if (QueueEmpty(lq))                //队空返回0
        return ;
    else
    {    p=lq->front;
        while (p!=NULL)
        {    printf("%s ",p->data);
            p=p->next;
        }
        printf("\n");
        return ;            //队不空返回1
    }
}

void main()
{    int sel,flag=;
    LQueue *lq;
    char name[];
    InitQueue(lq);            //初始化病人队列
    while (flag==)         //未下班时循环执行
    {    printf("1:排队 2:看医生 3:查看排队 0:下班  请选择:");
        scanf("%d",&sel);    //选择一项操作
        switch(sel)
        {
        case :                //医生下班
            if (!QueueEmpty(lq))
                printf("  >>请排队的患者明天就医\n");
            DestroyQueue(lq);
            flag=;
            break;
        case :                //一个病人排队
            printf("  >>输入患者姓名:");
            scanf("%s",name);
            EnQueue(lq,name);
            break;
        case :                //一个病人看医生
            if (!DeQueue(lq,name))
                printf("  >>没有排队的患者\n");
            else
                printf("  >>患者%s看医生\n",name);
            break;
        case :                //查看目前病人排队情况
            printf("  >>排队患者:");
            if (!DispQueue(lq))
                printf("  >>没有排队的患者\n");
            break;
        }
    }
}