angular4.x实现一个全选，反选，外加从下一页返回上一页，选中上一次的操作记录

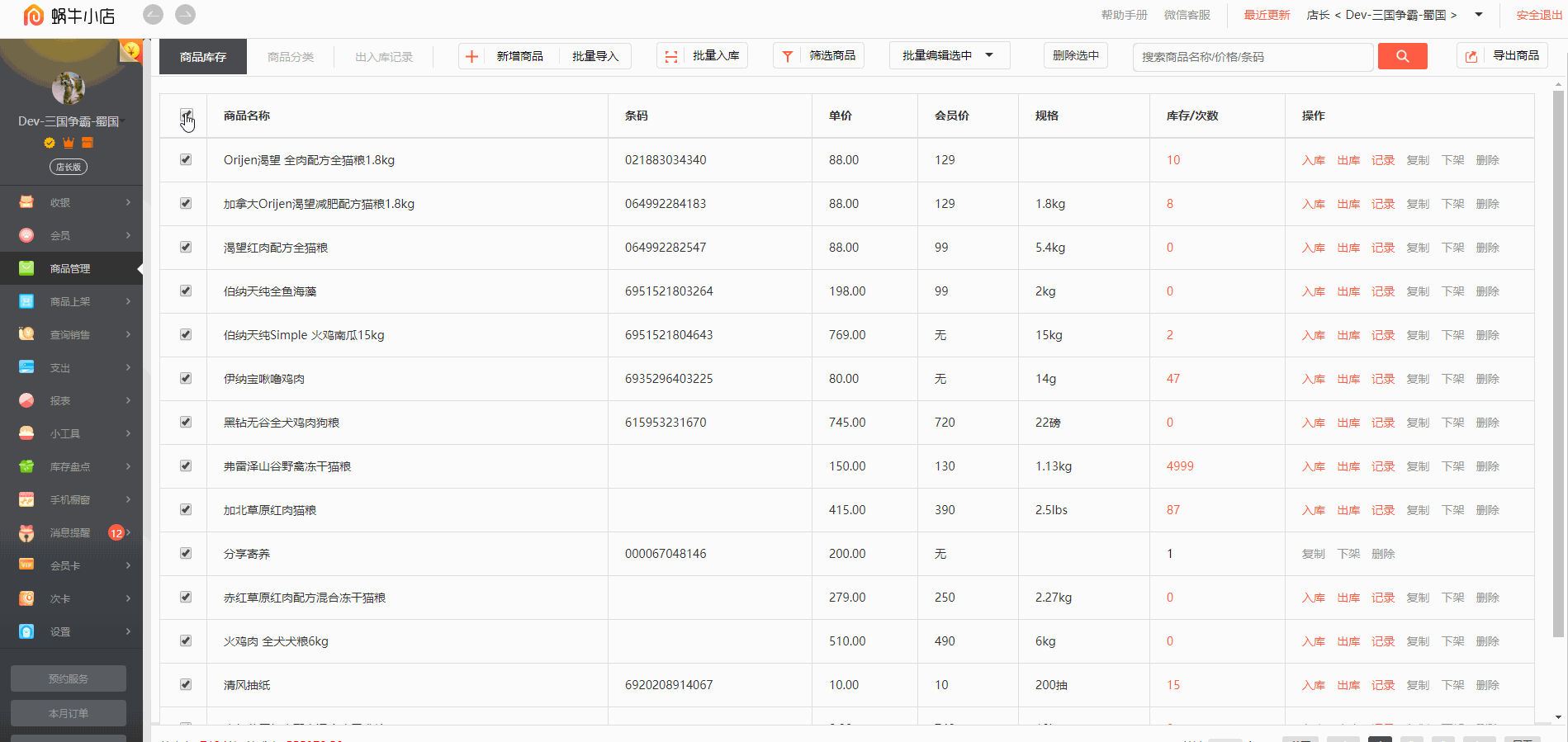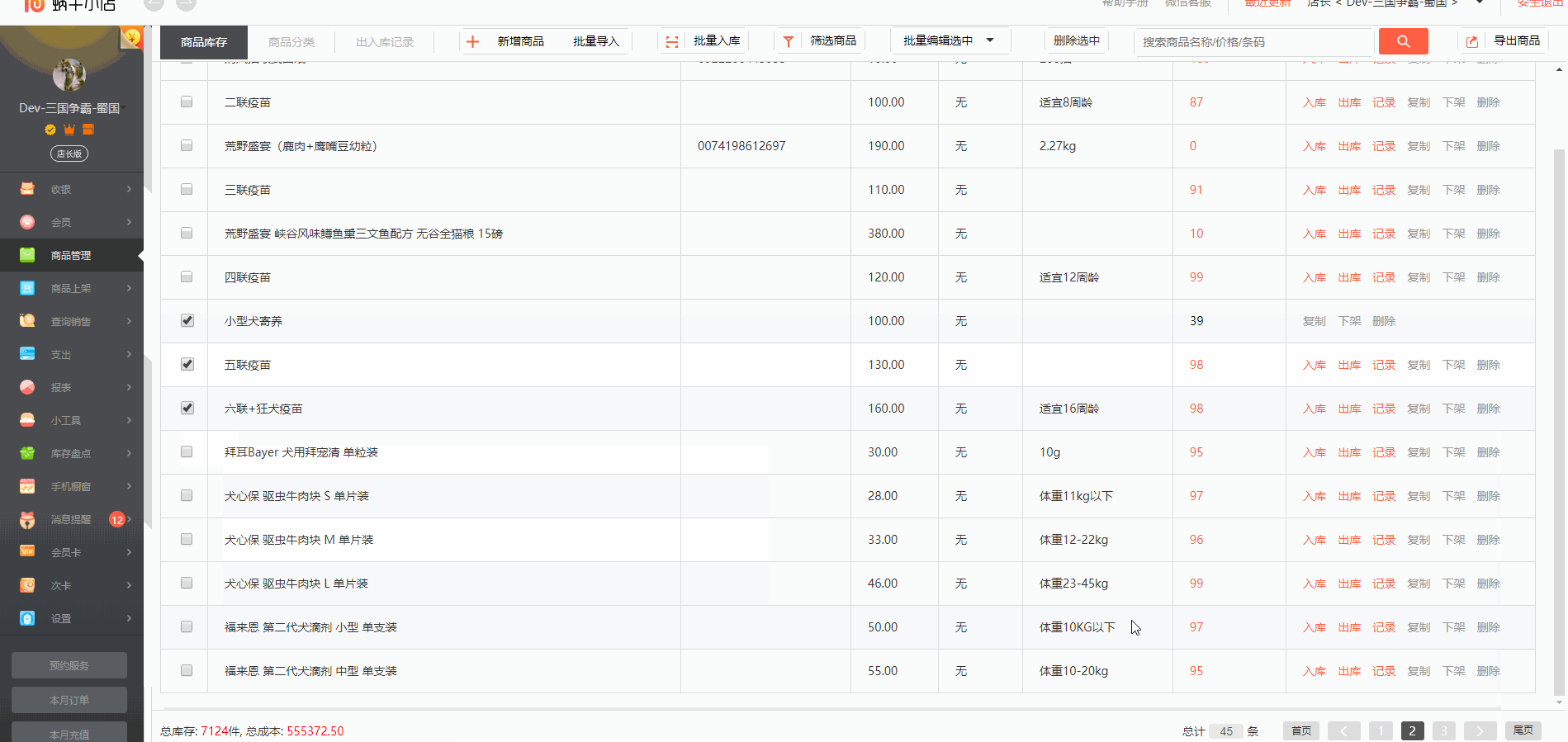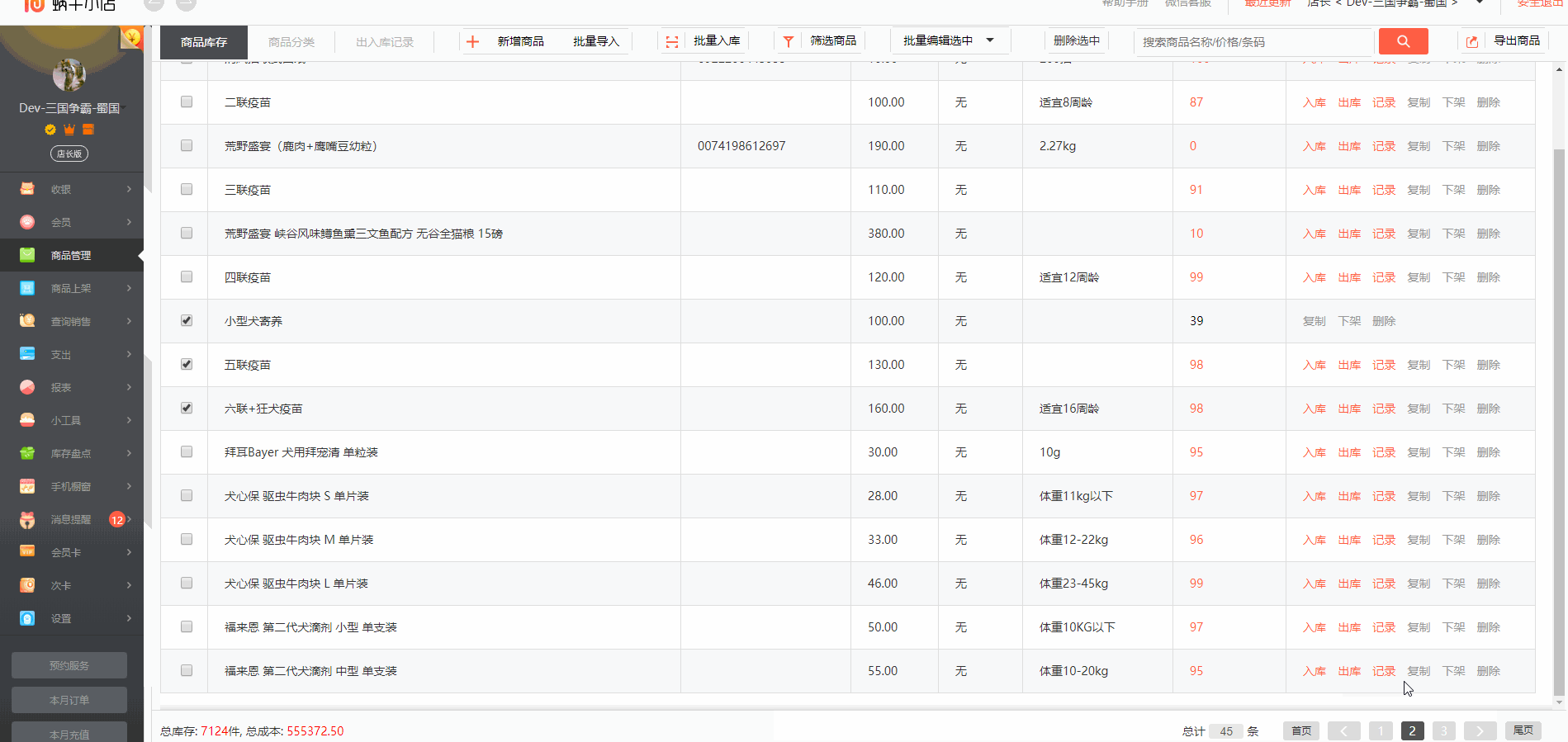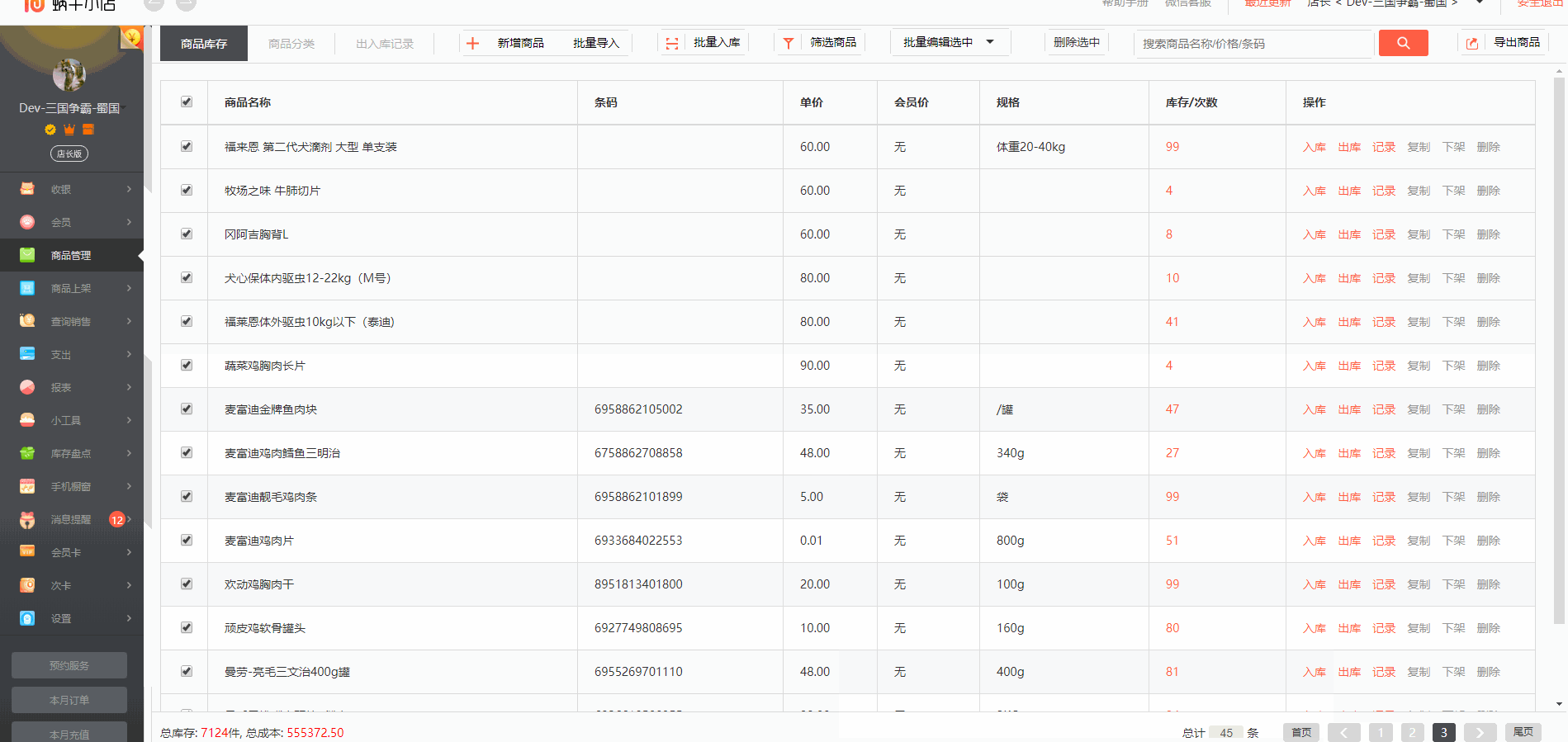
productMap:any = new Map<string, string>(); //定义一个map的数据模型
    //只要操作这个checkbox 那么只管把数据全部勾起了就行了 刷新数据源：products
    checkAll(page:any): void{

        //todo 取出用户当前是选中还是取消选中的标识
        let isTrue = $('#all_'+page).is(':checked');
        //let productMap = new Map();
        var tempArr = this.products;
        for(let item of tempArr){
            if(isTrue){
                item['checked'] = true;
                this.productMap.set(item.product_id, true);
            }else {
                item['checked'] = false;
                this.productMap.set(item.product_id, false);
            }

        }

        this.products = JSON.parse(JSON.stringify(tempArr)); //刷新数据源——这里需要深度拷贝界面才会动态刷新

        //console.log('tempArr',tempArr);
        console.log("this.products",this.products)
        console.log('checkAllproductMap',this.productMap);
    }

    //操作某一个checkbox框，做两件事：记录是否选中，去循环判断顶部的全选是否需要选中
    checkChange(obj):void{

        let tempArr = this.products;
        for(let item of tempArr){
            if(item.product_id === obj.product_id){
                let isFlag = !item.checked;
                item['checked']=!item.checked;
                this.productMap.set(item.product_id, isFlag);
            }

        }

        //返回一个新的数组，包含从 start 到 end （不包括该元素）的 arrayObject 中的元素。返回选定的元素，该方法不会修改原数组。
        let tempList = tempArr.slice(0,tempArr.length)
        this.products = tempList; //刷新数据源
        console.log('checkChangeproductMap',this.productMap);

        //todo 处理顶部按钮是否是全选的逻辑
        //let isChecked =
        let result = tempList.filter(item => {
            return item.checked ===true;
        })
        //debugger
        let pageNum = this.productList.pager.currentPage;
        if(result.length ===15){ //顶部的全选选中
            $("#all_"+pageNum).prop("checked",true);
        }else { //顶部的全选不选中
            $("#all_"+pageNum).attr("checked",false);
        }

    }

    //每次翻页的时候进行比对需要选中哪些数据
    pageChange():void{

        //从当前的15条数据中回显需要选中的数据，前置条件：如果本地的this.productMap有值
        let tempArr = this.products;
        for(let item of tempArr){
            item['checked'] = this.productMap.get(item.product_id)
        }

        let tempList = tempArr.slice(0,tempArr.length);
        let result = tempList.filter(item => {
            return item.checked ===true;
        })
        //debugger
        let pageNum = this.productList.pager.currentPage;
        if(result.length ===15){ //顶部的全选选中
            $("#all_"+pageNum).prop("checked",true);
        }else { //顶部的全选不选中
            $("#all_"+pageNum).attr("checked",false);
        }

        this.products = tempList;
    }