[Scikit-learn] 1.4 Support Vector Regression

SVM算法

既可用于回归问题，比如SVR(Support Vector Regression，支持向量回归）
也可以用于分类问题，比如SVC（Support Vector Classification，支持向量分类）

这里简单介绍下SVR：https://scikit-learn.org/stable/modules/svm.html#svm-regression

SVM解决回归问题

一、原理示范

感觉不是很好的样子，没有 Bayesian Linear Regression的效果好；但其实也是取决于“核”的选取。

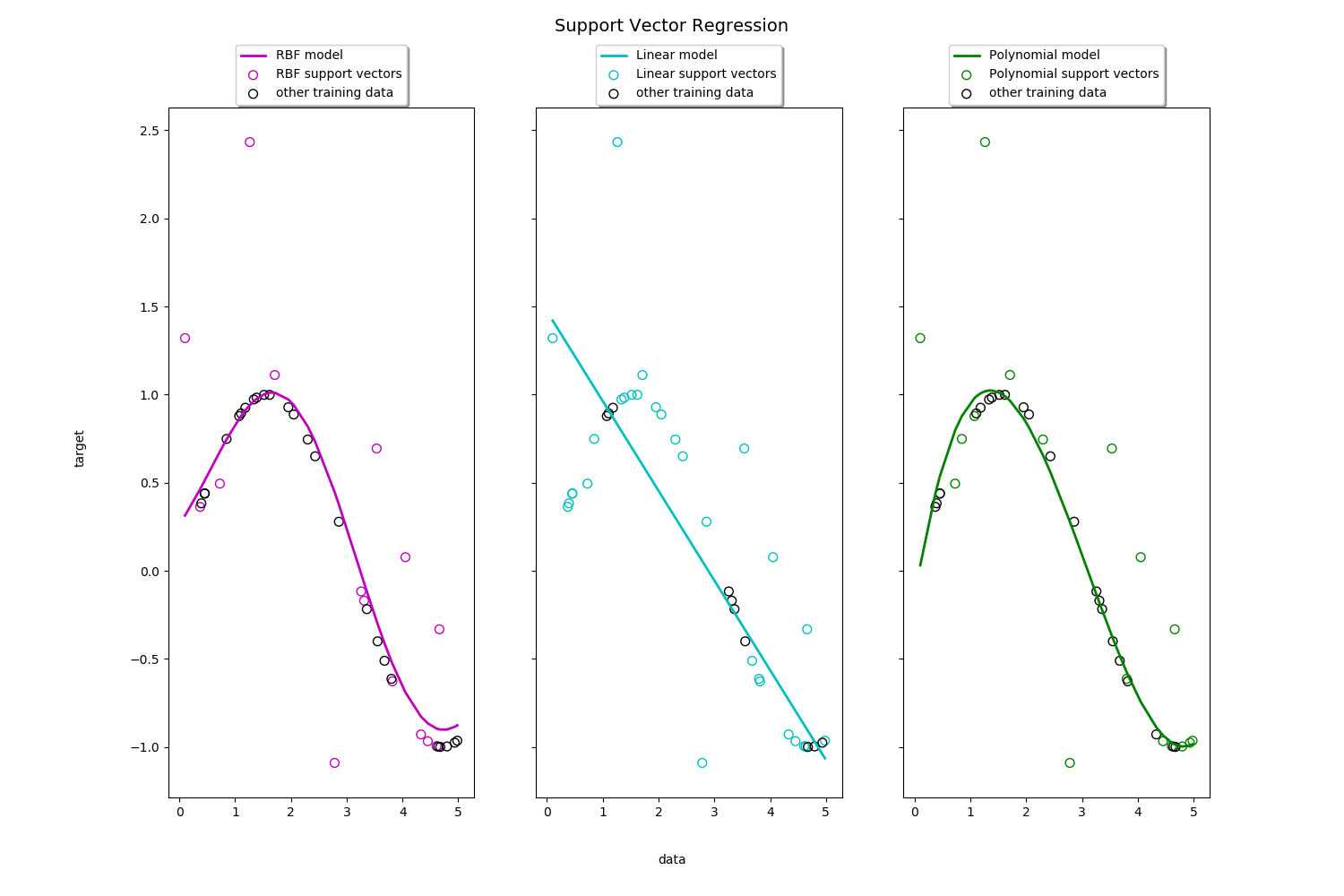
二、代码示范

print(__doc__)

import numpy as np

from sklearn.svm import SVR

import matplotlib.pyplot as plt

# #############################################################################

# Generate sample data

X = np.sort(5 * np.random.rand(40, 1), axis=0)

y = np.sin(X).ravel()

# #############################################################################

# Add noise to targets

y[::5] += 3 * (0.5 - np.random.rand(8))

# #############################################################################

# Fit regression model

svr_rbf  = SVR(kernel='rbf', C=100, gamma=0.1, epsilon=.1)

svr_lin  = SVR(kernel='linear', C=100, gamma='auto')

svr_poly = SVR(kernel='poly', C=100, gamma='auto', degree=3, epsilon=.1,

               coef0=1)

# #############################################################################

# Look at the results

lw = 2

svrs = [svr_rbf, svr_lin, svr_poly]

kernel_label = ['RBF', 'Linear', 'Polynomial']

model_color = ['m', 'c', 'g']

fig, axes = plt.subplots(nrows=1, ncols=3, figsize=(15, 10), sharey=True)

for ix, svr in enumerate(svrs):

    axes[ix].plot(X, svr.fit(X, y).predict(X), color=model_color[ix], lw=lw,

                  label='{} model'.format(kernel_label[ix]))

    axes[ix].scatter(X[svr.support_], y[svr.support_], facecolor="none",

                     edgecolor=model_color[ix], s=50,

                     label='{} support vectors'.format(kernel_label[ix]))

    axes[ix].scatter(X[np.setdiff1d(np.arange(len(X)), svr.support_)],

                     y[np.setdiff1d(np.arange(len(X)), svr.support_)],

                     facecolor="none", edgecolor="k", s=50,

                     label='other training data')

    axes[ix].legend(loc='upper center', bbox_to_anchor=(0.5, 1.1),

                    ncol=1, fancybox=True, shadow=True)

fig.text(0.5, 0.04, 'data', ha='center', va='center')

fig.text(0.06, 0.5, 'target', ha='center', va='center', rotation='vertical')

fig.suptitle("Support Vector Regression", fontsize=14)

plt.show()

可见，RBF有了径向基中“贝叶斯概率”的特性，跟容易找到数据趋势的主体。

实践出真知

Ref: SVM: 实际中使用SVM的一些问题

一、核的选择

如果features的范围差别不大。

- 一种选择是不使用kernel(也称为linear kernel)，直接使用x: 这种情况是当我们的n很大（即维度很高，features很多）但是训练样本却很少的情况下，我们一般不希望画出很复杂的边界线　(因为样本很少，画出很复杂的边界线就会过拟合)，而是用线性的边界线。
- 一种选择是使用Gaussian kernel：这种情况需要确定σ²(平衡bias还是variance)。这种情况是当x的维度不高，但是样本集很多的情况下。如上图中，n=2,但是m却很多，需要一个类似于圆的边界线。(即需要一个复杂的边界)

二、默塞尔定理

如果features的范围差别很大，在执行kernel之前要使用feature scaling。

我们最常用的是高斯kernel 和 linear kernel (即不使用kernel)，但是需要注意的是不是任何相似度函数都是有效的核函数，它们(包括我们常使用的高斯kernel)需要满足一个定理（默塞尔定理）,这是因为SVM有很多数值优化技巧，为了有效地求解参数Θ，需要相似度函数满足默塞尔定理，这样才能确保SVM包能够使用优化的方法来求解参数Θ。

三、LR / SVM / DNN 比较

我们将logistic regression的cost function进行了修改得出了SVM，那么我们在什么情况下应该使用什么算法呢？

【量少】如果我们的features要比样本数要大的话（如n=10000 (维度)，m=10-1000 (样本量)），我们使用logistic regression或者linear kernel，因为在样本较少的情况下，我们使用线性分类效果已经很好了，我们没有足够多的样本来支持我们进行复杂的分类。

【适量】如果n（维度）较小，m（样本量）大小适中的话，使用SVM with Gaussion kernel.如我们之前讲的有一个二维（n=2）的数据集，我们可以使用高斯核函数很好的将正负区分出来.

【量多】如果n（维度）较小，m（样本量）非常庞大的话，会创建一些features，然后再使用logistic regeression 或者linear kernel。因为当m非常大的话，使用高斯核函数会较慢。

logistic regeression 与linear kernel是非常相似的算法，如果其中一个适合运行的话，那么另一个也很有可能适合运行。

我们使用高斯kernel的范围很大，当m多达50000,n在1-1000(很常见的范围)，都可以使用SVM with 高斯kernel,可以解决很多logistic regression不能解决的问题。

神经网络在任何情况下都适用，但是有一个缺点是它训练起来比较慢，相对于SVM来说

SVM求的不是局部最优解，而是全局最优解

相对于使用哪种算法来说，我们更重要的是

1. 掌握更多的数据，
2. 如何调试算法（bias/variance），
3. 如何设计新的特征变量，

这些都比是使用SVM还是logistic regression重要。

但是SVM是一种被广泛使用的算法，并且在某个范围内，它的效率非常高，是一种有效地学习复杂的非线性问题的学习算法。

logistic regression,神经网络，SVM这三个学习算法使得我们可以解决很多前沿的机器学习问题。

End.