gcc 编译过程

gcc 编译过程
从 hello.c 到 hello(或 a.out)文件， 必须历经 hello.i、 hello.s、 hello.o，最后才得到 hello(或
a.out)文件，分别对应着预处理、编译、汇编和链接 4 个步骤，整个过程如图 10.5 所示。

这 4 步大致的工作内容如下：
（1） 预处理， C 编译器对各种预处理命令进行处理，包括头文件包含、宏定义的扩
展、条件编译的选择等；
（2） 编译，将预处理得到的源代码文件，进行“翻译转换”，产生出机器语言的目标
程序，得到机器语言的汇编文件；
（3） 汇编，将汇编代码翻译成了机器码，但是还不可以运行；
（4） 链接，处理可重定位文件，把各种符号引用和符号定义转换成为可执行文件中
的合适信息，通常是虚拟地址。

下面根据 hello.c 这个示例，跟踪一下其中的细节。
（1）预处理
在 gcc 命令加上-E 参数，可以得到预处理文件。输入下列命令：
vmuser@Linux-host:hello$ gcc -E hello.c –o hello.i
将会产生 hello.i 文件，这就是 hello.c 经过预处理后的文件。实际操作结果见图 10.6。

图 10.6 预编译得到 hello.i 文件
一个原本连同空行才 8 行的代码，经过预处理，得到了一个 800 多行的预处理文件，文
件开的内容如图 10.7 所示。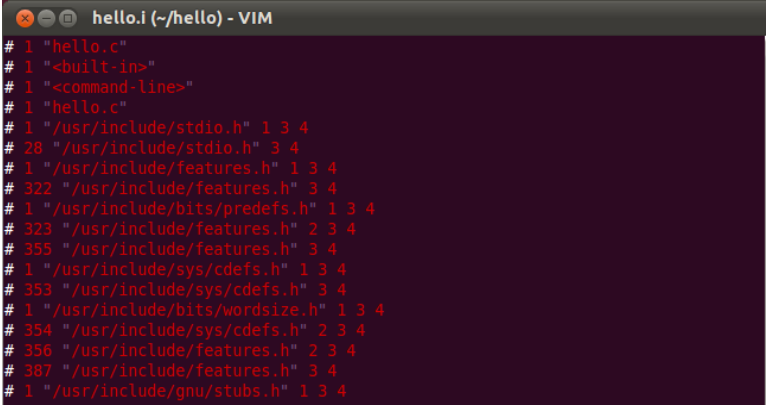

图 10.7 hello.i 文件开头
hello.i 文件末尾处的内容如图 10.8 所示。

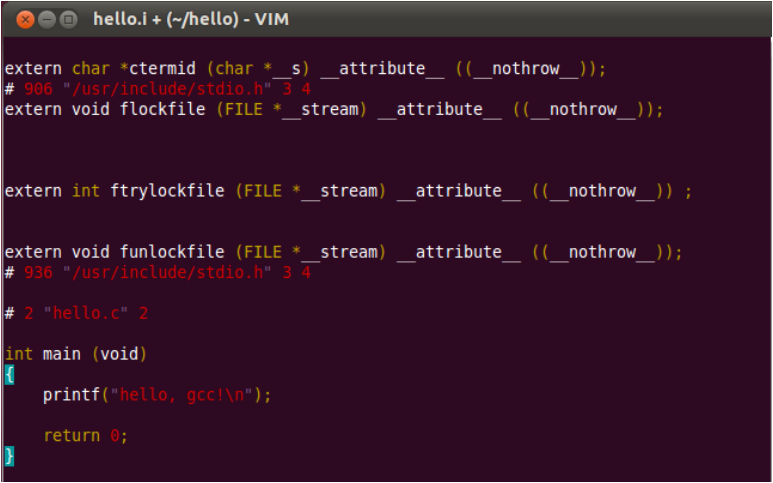
图 10.8 hello.i 文件末尾
其余部分内容请用 Vi 打开后进行查看。可以看到， hello.c 经过预处理后得到的 hello.i
文件，除了原本的几行代码之外，还包含了很多额外的变量、函数等等，这些都是预处理器
处理的结果。
（2）编译
在 gcc 编译参数加上-S，可以将 hello.i 编译成 hello.s 文件。命令如下：
vmuser@Linux-host:hello$ gcc -S hello.i

实际操作和结果如图 10.9 所示。

图 10.9 编译得到 hello.s 文件
hello.s 是一个汇编文件，可用 Vi 编辑器打开查看，如图 10.10 所示。

图 10.10 hello.s 文件内容
可以看到，该文件内容都是汇编语句。这里不对汇编进行解释。
（3）汇编
得到了汇编文件后，通过 gcc 就可以得到机器码了。在终端输入下列命令，可以得到
hello.o 文件。
vmuser@Linux-host:hello$ gcc -c hello.s
实际操作和结果如图 10.11 所示。

图 10.11 汇编得到 hello.o 文件
（4）链接
尽管已经得到了机器码，但这个文件却还是不可以运行的，必须要经过链接才能运行。
在终端输入下列命令，将会得到可执行文件 a.out。
vmuser@Linux-host:hello$ gcc hello.o
操作和结果如图 10.12 所示。

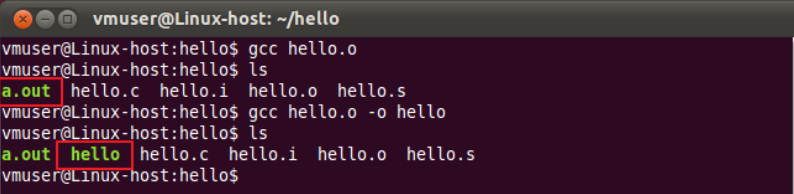
图 10.12 链接得到 a.out 文件
a.out 是 gcc 默认输出文件名称，可以通过-o 参数指定新的文件名。例如加上“-o hello”
参数，将会生成 hello 文件，这个文件和 a.out 实际上是一样的，用 md5sum 命令计算文件校
验值，两者完全一样，如图 10.13 所示。

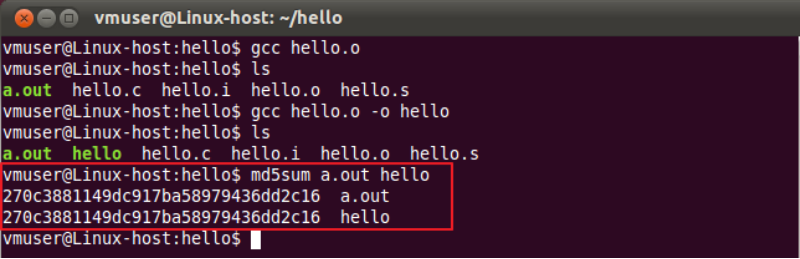
图 10.13 a.out 和 hello 文件
链接可分为动态链接和静态链接：
 动态链接使用动态链接库进行链接，生成的程序在执行的时候需要加载所需的动态
库才能运行。动态链接生成的程序小巧，但是必须依赖动态库，否则无法执行。
 Linux 下的动态链接库实际是共享目标文件（shared object），一般是.so 文件，
作用类似于 Windows 下的.dll 文件。
 静态链接使用静态库进行链接，生成的程序包含程序运行所需要的全部库，可以直
接运行，不过体积较大。
 Linux 下静态库是汇编产生的.o 文件的集合，一般以.a 文件形式出现。
gcc 默认是动态链接，加上-static 参数则采用静态链接。再来看 hello.c 示例，在链接的
时候加上-static 参数：
vmuser@Linux-host:hello$ gcc hello.o -static -o hello_static
操作命令和结果如图 10.14 所示，可以看到，动态链接生成的文件大小是 7155 字节，
而静态链接生成的文件却有 616096 字节，体积明显大了很多。

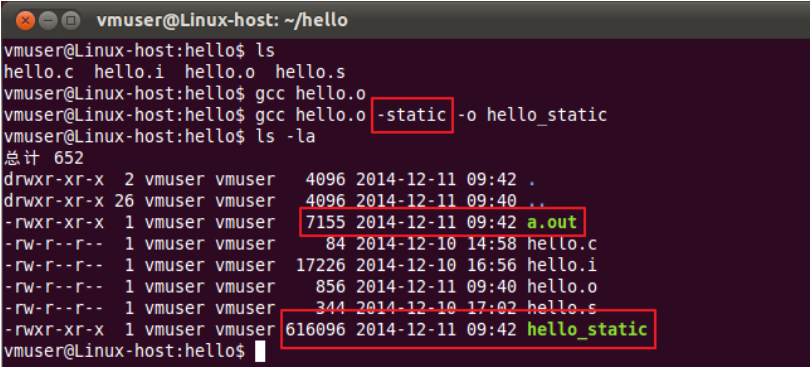
图 10.14 静态链接和动态链接结果对比