poj2826An Easy Problem?!

链接

繁琐细节题。

1、线段无交点时，ans=0;

2、如图 假设过p3.y的水平线与p1p2相交

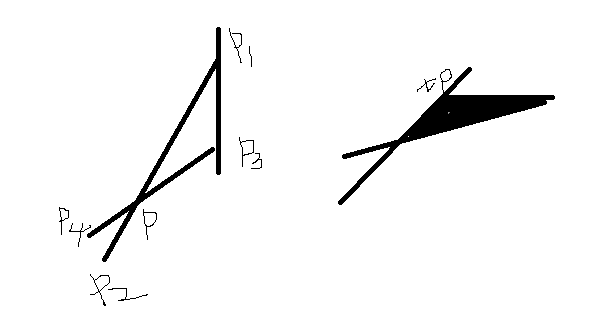
因为雨是垂直下落的，左图的情况是无法收集到雨水的，而这种情况有一种简便的判定方式 cross(p1-p2,p3-p4)与cross((p1+(0,1))-p1,p1,p3)同号

对于右边的，阴影部分即为ans,求出水平交点tp,p1p2与p3p4的交点pp,ans = fabs(cross(tp-pp,p3-pp))/2;

 #include <iostream>
 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 #include<stdlib.h>
 #include<vector>
 #include<cmath>
 #include<queue>
 #include<set>
 using namespace std;
 #define N 100000
 #define LL long long
 #define INF 0xfffffff
 const double eps = 1e-;
 const double pi = acos(-1.0);
 const double inf = ~0u>>;
 struct point
 {
     double x,y;
     point(double x=,double y=):x(x),y(y) {}
 } p[];
 typedef point pointt;
 pointt operator -(point a,point b)
 {
     return pointt(a.x-b.x,a.y-b.y);
 }
 int dcmp(double x)
 {
     if(fabs(x)<eps) return ;
     return x<?-:;
 }
 double cross(point a,point b)
 {
     return a.x*b.y-a.y*b.x;
 }
 bool cmp(point a,point b)
 {
     return a.y>b.y;
 }

 bool intersection1(point p1, point p2, point p3, point p4, point& p)      // 直线相交
 {
     double a1, b1, c1, a2, b2, c2, d;
     a1 = p1.y - p2.y;
     b1 = p2.x - p1.x;
     c1 = p1.x*p2.y - p2.x*p1.y;
     a2 = p3.y - p4.y;
     b2 = p4.x - p3.x;
     c2 = p3.x*p4.y - p4.x*p3.y;
     d = a1*b2 - a2*b1;
     if (!dcmp(d))    return false;
     p.x = (-c1*b2 + c2*b1) / d;
     p.y = (-a1*c2 + a2*c1) / d;
     return true;
 }
 double solve(point p1,point p2,point p3,point p4,point pp,point tp)
 {
     double ans;
     point p11 = point(p1.x,p1.y+);
     if(dcmp(cross(p11-p1,p1-p3))==)
     {
         ans = ;
         //cout<<",";
     }
     else
     {
         if(dcmp(cross(p11-p1,p1-p3))*dcmp(cross(p1-p2,p3-p4))<)
         {
             ans = fabs(cross(p3-pp,tp-pp))/;
             //cout<<",";
         }
         else ans = ;
     }
     return ans;
 }
 int on_segment( point p1,point p2 ,point p )
 {
     double max=p1.x > p2.x ? p1.x : p2.x ;
     double min =p1.x < p2.x ? p1.x : p2.x ;
     double max1=p1.y > p2.y ? p1.y : p2.y ;
     double min1=p1.y < p2.y ? p1.y : p2.y ;
     if( p.x >=min && p.x <=max &&
             p.y >=min1 && p.y <=max1 )
         return ;
     else
         return ;
 }
 int main()
 {
     int t,i;
     cin>>t;
     while(t--)
     {
         for(i = ; i <=  ; i++)
             scanf("%lf%lf",&p[i].x,&p[i].y);
         sort(p+,p+,cmp);
         sort(p+,p+,cmp);
         point pp;
         if(intersection1(p[],p[],p[],p[],pp))
         {
             if(!on_segment(p[],p[],pp)||!on_segment(p[],p[],pp))
             {
                 puts("0.00");
                 continue;
             }
         }
         //cout<<pp.x<<" "<<pp.y<<endl;
         double ans;
         point p1 = point(p[].x-,p[].y),p2;
         point p3 = point(p[].x-,p[].y);
         if(intersection1(p[],p[],p[],p1,p2)&&on_segment(p[],p[],p2))
         {

             ans = solve(p[],p[],p[],p[],pp,p2);
         }
         else
         {
             intersection1(p[],p[],p[],p3,p2);
            // cout<<p2.x<<" "<<p2.y<<endl;
             ans = solve(p[],p[],p[],p[],pp,p2);
         }
         printf("%.2f\n",ans+eps);

     }
     return ;
 }