hdu---(3779)Railroad(记忆化搜索/dfs)

Railroad

Time Limit: 4000/2000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 572    Accepted Submission(s): 228

Problem Description

A
train yard is a complex series of railroad tracks for storing, sorting,
or loading/unloading railroad cars. In this problem, the railroad
tracks are much simpler, and we are only interested in combining two
trains into one.

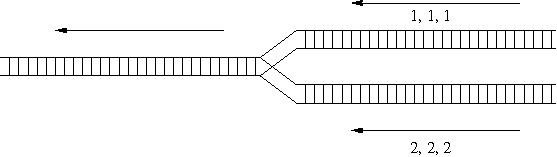
Figure 1: Merging railroad tracks.

The
two trains each contain some railroad cars. Each railroad car contains a
single type of products identified by a positive integer up to
1,000,000. The two trains come in from the right on separate tracks, as
in the diagram above. To combine the two trains, we may choose to take
the railroad car at the front of either train and attach it to the back
of the train being formed on the left. Of course, if we have already
moved all the railroad cars from one train, then all remaining cars from
the other train will be moved to the left one at a time. All railroad
cars must be moved to the left eventually. Depending on which train on
the right is selected at each step, we will obtain different
arrangements for the departing train on the left. For example, we may
obtain the order 1,1,1,2,2,2 by always choosing the top train until all
of its cars have been moved. We may also obtain the order 2,1,2,1,2,1 by
alternately choosing railroad cars from the two trains.

To
facilitate further processing at the other train yards later on in the
trip (and also at the destination), the supervisor at the train yard has
been given an ordering of the products desired for the departing train.
In this problem, you must decide whether it is possible to obtain the
desired ordering, given the orders of the products for the two trains
arriving at the train yard.

 

Input

The input consists of a number of cases. The first line contains two positive integers N₁ N₂
which are the number of railroad cars in each train. There are at least
1 and at most 1000 railroad cars in each train. The second line
contains N1 positive integers (up to 1,000,000) identifying the products
on the first train from front of the train to the back of the train.
The third line contains N₂ positive integers identifying the products on the second train (same format as above). Finally, the fourth line contains N₁+N₂ positive integers giving the desired order for the departing train (same format as above).

The end of input is indicated by N₁ = N₂ = 0.

 

Output

For each case, print on a line possible if it is possible to produce the desired order, or not possible if not.

 

Sample Input

3 3
1 2 1
2 1 1
1 2 1 1 2 1
3 3
1 2 1
2 1 2
1 1 1 2 2 2
0 0

 

Sample Output

possible

not possible

 

题目的意思：  给你两个数组a,b  让a,b两个数组按其原序进行组合，问能否组合成为c数组。

 

我们可以试着用搜索的方式进行处理，但是由于数据较大，而且在处理的过程中，有重叠的状态，所以我们需要用到记忆话，对于原先有的状态之后的搜索，我们不去在重复，这样就节省了很多的时间。

代码：

 //#define LOCAL
 #include<cstdio>
 #include<cstring>
 using namespace std;
 const int maxn=;
 int aa[maxn],bb[maxn],cc[maxn<<];
 int mat[maxn][maxn];
 int n1,n2;
 bool flag;
 void dfs(int lena,int lenb,int lenc)
 {
     if(lena==n1+&&lenb==n2+){
          flag=;
         return ;
      }
    if(mat[lena][lenb]) return ;
    if(!flag&&aa[lena]==cc[lenc]){
        mat[lena][lenb]=;
          dfs(lena+,lenb,lenc+);
    }
    if(!flag&&bb[lenb]==cc[lenc]){
        mat[lena][lenb]=;
       dfs(lena,lenb+,lenc+);
    }
 }
 void input(int n,int a[])
 {
     for(int i=;i<=n;i++)
        scanf("%d",&a[i]);
 }
 int main()
 {
     #ifdef LOCAL
     freopen("test.in","r",stdin);
     #endif
     while(scanf("%d%d",&n1,&n2)&&n1+n2!=)
     {
         input(n1,aa);
         aa[n1+]=-;
         input(n2,bb);
         bb[n2+]=-;
         input(n1+n2,cc);
         flag=;
         memset(mat,,sizeof(mat));
         dfs(,,);
         if(flag)printf("possible\n");
         else printf("not possible\n");
     }
  return ;
 }