zay大爷的膜你题 D2T1 江城唱晚

二更——

因为这篇题解在zay讲之前就写完了，所以我就没写前面的骗分做法，取而代之的是对于正解的一些补充

依旧是外链。。。

这一次网易云爆炸了。。。。所以我决定后面的都用QQ（后续的题解证明我真香了）

下面是题面

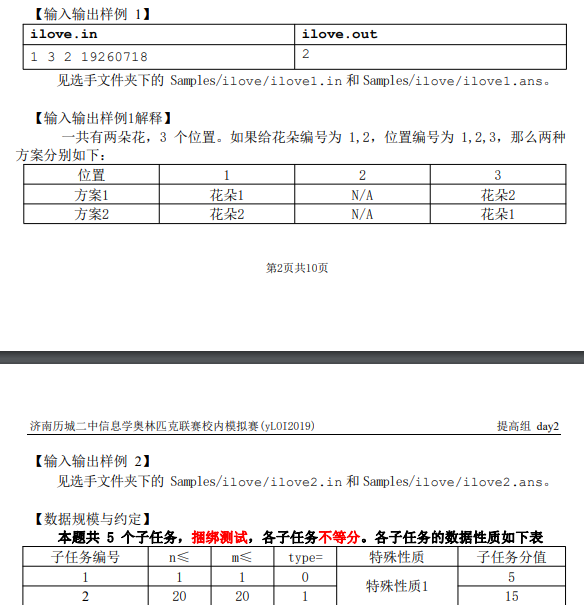
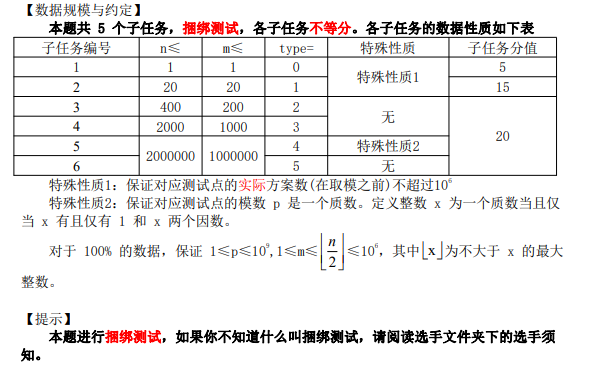
这道题是一道傻逼题 数学题，按照zay的说法，这种题目在数据范围比较小的情况下可以用dp，数据比较大的话就得用组合数学等方法纸面上推了

我们仔细看一看，首先有m朵花的话，我们就有m！种排列方式（也就是m的全排列），然后我们假设已经把花的顺序排好了

我们这一步要做的事情就是在剩下的n-m+1个空中选择m个插到m朵花中去，也就是插空算法，至于在算n-m等数组要不要+1的时候，最好还是手推再加上实践，这样能保证算出来的数是正确的

所以最后的答案就是A(m,m)*C(n-m+1,m)

本来以为按A和C的算法直接写上就没事的，但是我们忽略了一个问题，直接算阶乘太大，在模意义下算除法还得求逆元，这就意味着我们得化简，把整个式子写出来然后化简得到

(n-m+1)! / (n-2m+1)!

然后直接从n-2m+2开始循环就可以啦

这是代码

#include <iostream>
#include <cstdio>
#include <cmath>
using namespace std;
long long type, n, m, p, ans = ;
int main()
{
    freopen("ilove.in","r",stdin);
    freopen("ilove.out","w",stdout);
    scanf("%lld%lld%lld%lld", &type, &n, &m, &p);
    if(type == ){
        printf("");
        return ;
    }
    if(n < m*-){
        printf("");
        return ;
    }
    for (int i = n - *m + ; i <= n - m + ; ++i){
        ans = ans * i % p;
    }
    printf("%lld", ans % p);
    return ;
}

对了，还有一个事，虽然我们对这个东西取模，但是还是很容易溢出int，所以在输出等时候，我们最好是开一个long long

最后送上一句话

十年OI一场空，不开long long见祖宗