51nod 1116 K进制下的大数
你万万想不到,Long Long 就能存下的数据
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <map>
using namespace std;
typedef long long ll;
map<char,int>mp;
int main()
{ string s;
while(cin>>s){
int max1=-1;
int max2=-1;
bool flag=false;
bool kk=false;
for(int i=0;i<s.length();i++){
if(s[i]>='A'&&s[i]<='Z')
{flag=true;
max2=max(max2,s[i]-'A');
}
else if(s[i]>='0'&&s[i]<='9')
max1=max(max1,s[i]-'0');
}
if(!flag){
for(int i=max1+1;i<=36;i++){
ll k=1;
ll sum=0;
for(int j=0;j<s.length();j++){
sum=sum*i+1ll*(s[j]-'0');
sum%=(i-1);
}
if(!sum)
{printf("%d\n",i);kk=true;break;}
}
}
else{
for(int i=max2+11;i<=36;i++){
ll k=1;
ll sum=0;
for(int j=0;j<s.length();j++){
if(s[j]>='0'&&s[j]<='9')
sum =1ll*(s[j]-'0')+sum*i;
else
sum=1ll*(s[j]-'A'+10)+sum*i;
sum%=(i-1);
}
//if(i==22)
//cout<<sum<<"@@@@"<<endl;
if(!sum)
{printf("%d\n",i);
//cout<<"!!"<<max2+11<<endl;
//cout<<sum<<endl;
//cout<<(i-1)<<endl;
kk=true;
break;}
}
}
if(!kk)
puts("No solution");
}
return 0;
}51nod 1116 K进制下的大数的更多相关文章
- 51nod 1116 K进制下的大数 (暴力枚举)
题目链接 题意:中文题. 题解:暴力枚举. #include <iostream> #include <cstring> using namespace std; ; ; ch ...
- 51Nod 1116 K进制下的大数(暴力枚举)
#include<iostream> #include<cstdio> #include<algorithm> #include<cstring> us ...
- 51 Nod 1116 K进制下的大数
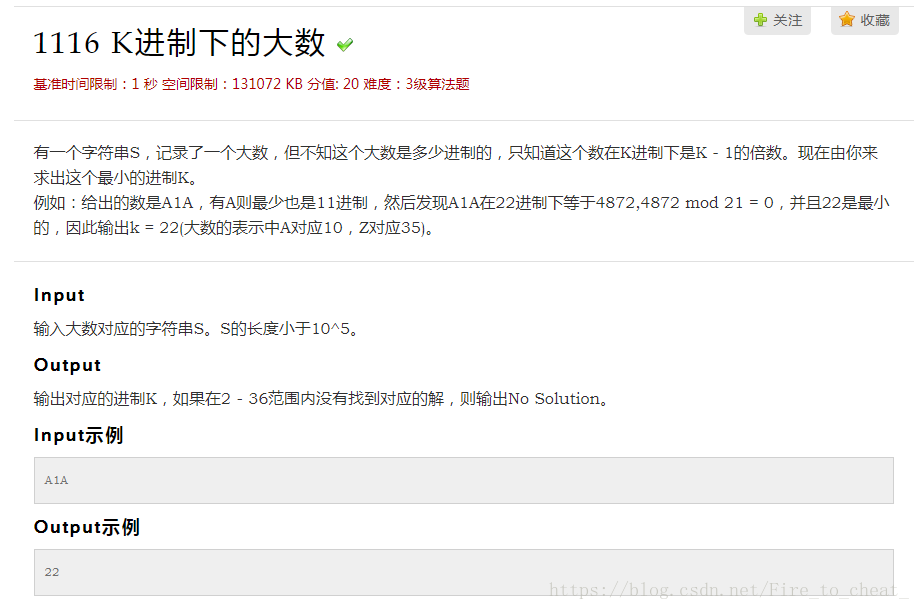
1116 K进制下的大数 基准时间限制:1 秒 空间限制:131072 KB 分值: 20 难度:3级算法题 收藏 关注 有一个字符串S,记录了一个大数,但不知这个大数是多少进制的,只知道这个数 ...
- [51nod1116]K进制下的大数
解题关键:$A\% (k - 1) = (A[0] + A[1]*k + A[2]*{k^2} + ...A[n]*{k^n})\% (k - 1) = (A[0] + A[1] + ...A[n]) ...
- A - K进制下的大数
https://vjudge.net/contest/218366#problem/A 中间溢出,注意求模. #include<iostream> #include<cstdio&g ...
- n!在k进制下的后缀0
问n! 转化成k进制后的位数和尾数的0的个数.[UVA 10061 How many zeros and how many digits?] Given a decimal integer numbe ...
- bzoj 3000 Big Number 估算n!在k进制下的位数 斯特林公式
题目大意 求n!在k进制下的位数 2≤N≤2^31, 2≤K≤200 分析 作为数学没学好的傻嗨,我们先回顾一下log函数 \(\log_a(b)=\frac 1 {log_b(a)}\) \(\lo ...
- 求x!在k进制下后缀零的个数(洛谷月赛T1)
求x!在k进制下后缀和的个数 20分: 求十进制下的x!后缀和的个数 40分: 高精求阶乘,直接模拟过程 (我不管反正我不打,本蒟蒻最讨厌高精了) 60分 利用一个定理(网上有求x!在 ...
- 陕西师范大学第七届程序设计竞赛网络同步赛 F WWX的礼物【数学/k进制下x^n的位数/log】
链接:https://www.nowcoder.com/acm/contest/121/F来源:牛客网 题目描述 WWX的女朋友送给了他一个礼物,可是礼物却被一把K进制密码锁锁住了.在礼物盒上还有一张 ...
随机推荐
- System表空间大小有10Gb,使用率达到95%,
System表空间大小有10Gb,使用率达到95%,很好奇, 随后执行如下SQL,查看system表空间中使用空间最多的对象 SQL>SELECT * FROM DBA_SEGMENTS T W ...
- Nginx: 解决connect() to xxxx failed (13: Permission denied) while connecting to upstream的问题
一句话:setsebool httpd_can_network_connect true
- 基于github for windows&github的团队协作基本操作
首先,我们要在github上团队协作.先要建立一个team.这个自行百度,在github上操作就是. 点击打开链接 这是我的有道文章(假设看不到图片的话) 今天主要讲的是怎么操作github for ...
- KindEditor使用过程中,用JQ提交表单时,获取不到编辑器的内容
首先要说明的是.在使用提交button直接提交时.编辑器的内容是能够正常获取的,而使用 jq或js ,如$("#form").submit(),提交时,则编辑器的内容是无法获取的. ...
- Spring中AOP的使用
问题:什么是AOP? 答:AOP基本概念:Aspect-Oriented Programming,面向方面编程的简称,Aspect是一种新的模块化机制.用来描写叙述分散在对象.类或方法中的横切关注点( ...
- java8--IO工具类(java疯狂讲义3复习笔记)
Paths类 public static void pathTest(){ Path path = Paths.get("~"); System.out.println(path) ...
- Linux Find Out Last System Reboot Time and Date Command 登录安全 开关机 记录 帐号审计 历史记录命令条数
Linux Find Out Last System Reboot Time and Date Command - nixCraft https://www.cyberciti.biz/tips/li ...
- YTU 2430: C语言习题 链表建立,插入,删除,输出
2430: C语言习题 链表建立,插入,删除,输出 时间限制: 1 Sec 内存限制: 128 MB 提交: 576 解决: 280 题目描述 编写一个函数creatlink,用来建立一个动态链表 ...
- YTU 2562: 黄金螺旋
2562: 黄金螺旋 时间限制: 1 Sec 内存限制: 128 MB 提交: 832 解决: 427 题目描述 黄金螺旋是根据斐波那契数列画出来的螺旋曲线,自然界中存在许多斐波那契螺旋线的图案, ...
- Masonry scrollview循环布局
前言 说到iOS自动布局,有很多的解决办法.有的人使用xib/storyboard自动布局,也有人使用frame来适配.对于前者,笔者并不喜欢,也不支持.对于后者,更是麻烦,到处计算高度.宽度等,千万 ...