【阶梯报告】洛谷P3391【模板】文艺平衡树 splay

【阶梯报告】洛谷P3391【模板】文艺平衡树 splay

题目链接在这里[链接](https://www.luogu.org/problemnew/show/P3391)
最近在学习splay，终于做对了这道模版题，虽然不是很难的样子。~~但是我一开始并不会做，而且看完题解之后还打错一直打不对，调试了很久~~
下面是题目简述

现在给你一个长度为n的序列，序列元素初始为1,2,3...n，同时有m个操作，每个操作给定一个L和R，表示将[L,R]区间的数进行翻转。
输出：完成所有操作之后的序列（n,m≤100000）

首先，这道题用暴力是肯定超时的。但是既然连题目都提示用splay做这道题了，那么我们自然可以用splay做这道题。
首先我们想一下splay的树的性质。
### 性质
1. 如果我们给每一个点添加一个键值，这个键值表示的是这个点在序列中的位置，那么我们对splay树进行中序遍历之后，得到的序列就是原来对应的序列。
2. 对于splay树，无论是进行zip还是zap操作，都不会影响最终中序遍历的结果。因为zip和zap都是在保证二叉查找树的性质的前提下进行的。
3. 假如我们splay(L-1,root),然后，splay(R+1,root->right_child),那么我们就会惊奇地发现，区间[L,R]内的所有点都在R+1这个结点的左子树种。
4. 假如我们把任意一个结点的子树中的每一个结点的左右子树都换边，（包括自己）那么最终中序遍历的结果就是——除了被翻转的子树以外，其他所有点的中序遍历都没有变化，而子树中的所有节点（包括子树根节点）的中序遍历刚刚好反了过来。（你们可以自己画一个图试一下，或者说，如下图）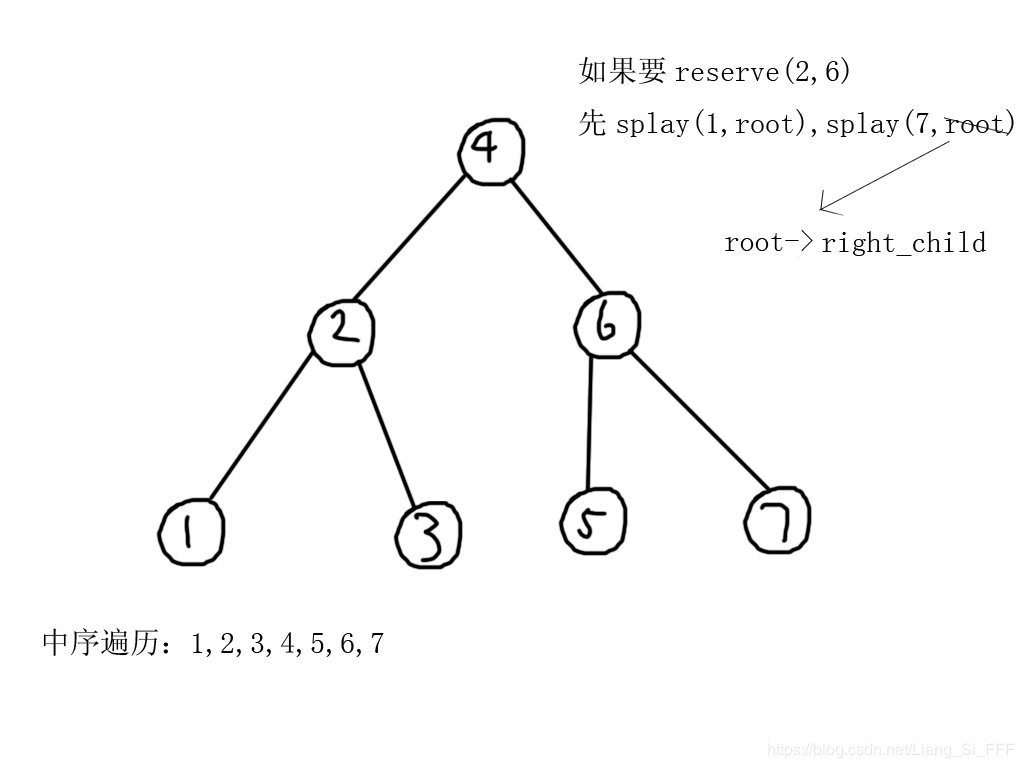

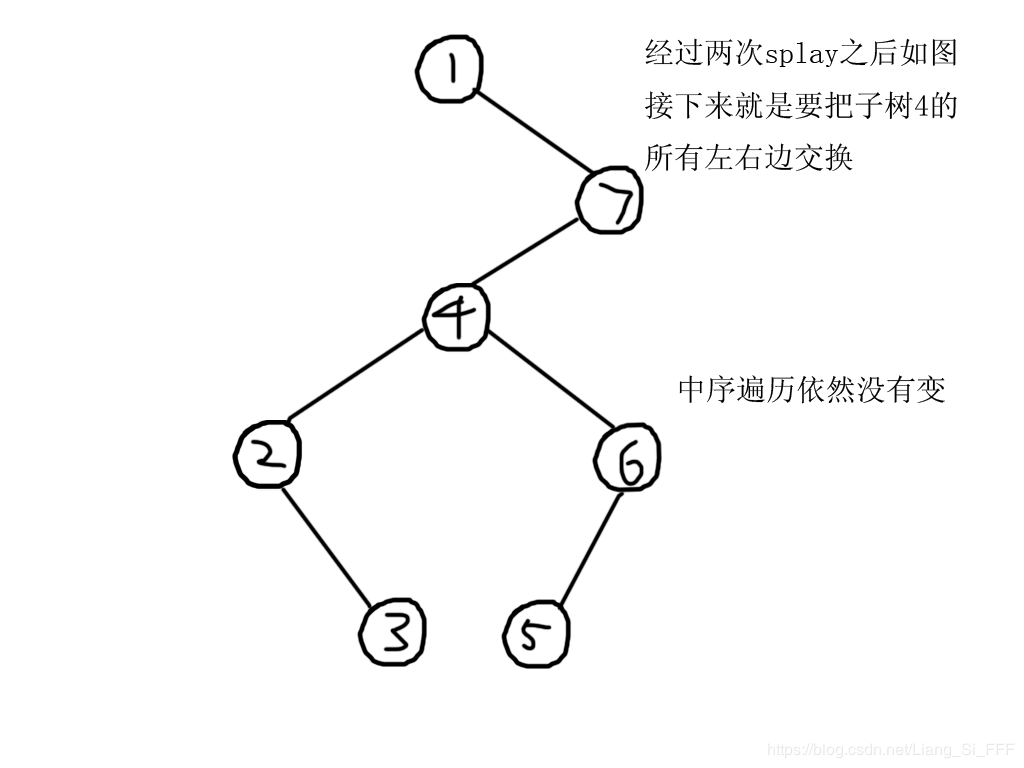
思路
第一种简陋的想法
1. 以1,2,3,4...n为键值插入splay树（或者直接构建一棵平衡树就行，因为你已经知道会有哪些元素插入树中）。之后，我们对树的所有操作都不需要用到键值，直接根据zip和zap不会改变中序遍历的特性进行改变。
2. 翻转区间的时候，先splay(l-1,root),splay(r+1,root->right_child)，然后再把r+1这个结点的左子树的所有左右孩子交换即可。

虽然这么做确实可以做对题目，但是这样会有几个需要注意的地方。
1 . 假如要reserve(1,n),那么我们将会splay(0,root)和splay(n+1,root->left_child),但是树中没有0和n+1这两个结点。因此一开始的时候我们就应该加入INF和-INF，充当卫兵的作用。
2 . 交换子树中所有结点的速度实在是太慢了，和o(n)压根没有区别。这样根本就没有变快。
优化的方法
1. 翻转树的时候不需要把整个子树都交换，只要采取线段树的懒标记的方法做一个标记即可。
- 标记完之后，假如等一下再标记同样的区间，只要异或一下1就可以了
- 假如要splay的点在已经翻转过的子树里面，那么我们到时候只要在寻找结点的过程中进行push_down就可以了。
- 在输出整棵splay树的时候，也注意一下push_down就可以了。
具体方法
1. 把所有的元素都塞进splay里面。由于一开始就是有序的，所以你既可以一个一个地insert进去，也可以直接就构建一个十分平衡的splay树
2. 对于每一个翻转操作，首先splay(l-1,root),splay(r+1,root->right_child),然后再把r+1的左子树打上标记即可
3. 要点：每次在find一个结点的时候，一定要先push_down,然后再进行操作。
4. 最后输出整棵树的时候也注意一下push_down
下面是我的代码，可能不是很看得明白。

 #include<cstdio>
 using namespace std;
 const int N=;
 const int INF=;
 struct node
 {
 int lc,rc,fa,size,val,mark;//mark就是懒标记，val是本来的值,size是子树（包括自己）的大小
 node()
 {
 lc=rc=fa=size=val=mark=;
 }
 }tree[N];
 int root=,tot=,FIRST=;
 void build(int,int,int,int);//直接用递归在刚开始的时候建立一棵比较平衡的树
 void push_down(int);
 void zip(int);//左旋
 void zap(int);//右旋
 void initailize();//放入INT和-INF作为卫兵
 void splay(int,int);
 int find(int);//用于寻找splay树中的第几大的数。毕竟在序列中排第k的数就是在splay中第k大的数
 void reverse(int,int);
 void print(int);//用递归输出整棵树
 int main()
 {
 int n,m;
 scanf("%d%d",&n,&m);
 build(,,n,);
 initailize();
 while(m--)
 {
 int l,r;
 scanf("%d%d",&l,&r);
 reverse(l+,r+);//由于有-INF的存在，所以翻转[l,r]区间的时候，其实是翻转[l+1,r+1]区间
 }
 print(root);
 return ;
 }
 void build(int x,int l,int r,int father)
 {
 tree[x].fa=father;
 tree[x].size=;
 if(l==r)
 {
 tree[x].val=l;
 return;
 }
 int mid=(l+r)/;
 tree[x].val=mid;
 if(mid==l)
 {
 tree[x].rc=++tot;
 build(tot,r,r,x);
 tree[x].size+=tree[tree[x].rc].size;
 }
 else
 {
 tree[x].lc=++tot;
 build(tot,l,mid-,x);
 tree[x].rc=++tot;
 build(tot,mid+,r,x);
 tree[x].size+=tree[tree[x].lc].size+tree[tree[x].rc].size;
 }
 }
 void initailize()
 {
 int p=root;
 while(tree[p].lc!=) tree[p].size++,p=tree[p].lc;
 tree[p].size++;
 tree[p].lc=++tot;
 tree[tot].fa=p;
 tree[tot].size=;
 tree[tot].val=-INF;
 p=root;
 while(tree[p].rc!=) tree[p].size++,p=tree[p].rc;
 tree[p].size++;
 tree[p].rc=++tot;
 tree[tot].fa=p;
 tree[tot].size=;
 tree[tot].val=INF;
 }
 void inline push_down(int x)
 {
 if(tree[x].mark)
 {
 int L=tree[x].lc,R=tree[x].rc;
 tree[L].mark^=;
 tree[R].mark^=;
 tree[x].mark=;
 tree[x].lc=R;
 tree[x].rc=L;
 }
 }
 void zip(int x)
 {
 int y=tree[x].fa;
 tree[y].rc=tree[x].lc;
 tree[x].lc=y;
 tree[x].fa=tree[y].fa;
 tree[y].fa=x;
 if(tree[x].fa)
 if(tree[tree[x].fa].lc==y)
 tree[tree[x].fa].lc=x;
 else tree[tree[x].fa].rc=x;
 else root=x;
 if(tree[y].rc)
 tree[tree[y].rc].fa=y;
 tree[y].size=tree[tree[y].lc].size+tree[tree[y].rc].size+;
 tree[x].size=tree[tree[x].lc].size+tree[tree[x].rc].size+;
 }
 void zap(int x)
 {
 int y=tree[x].fa;
 tree[y].lc=tree[x].rc;
 tree[x].rc=y;
 tree[x].fa=tree[y].fa;
 tree[y].fa=x;
 if(tree[x].fa)
 if(tree[tree[x].fa].lc==y)
 tree[tree[x].fa].lc=x;
 else tree[tree[x].fa].rc=x;
 else root=x;
 if(tree[y].lc)
 tree[tree[y].lc].fa=y;
 tree[y].size=tree[tree[y].lc].size+tree[tree[y].rc].size+;
 tree[x].size=tree[tree[x].lc].size+tree[tree[x].rc].size+;
 }
 void splay(int x,int aim)
 {
 aim=tree[aim].fa;
 while(tree[x].fa!=aim)
 {
 int y=tree[x].fa;
 int z=tree[y].fa;
 if(z==aim)
 if(tree[y].lc==x)
 zap(x);
 else zip(x);
 else if(tree[z].lc==y&&tree[y].lc==x)
 zap(x),zap(x);
 else if(tree[z].rc==y&&tree[y].rc==x)
 zip(x),zip(x);
 else if(tree[z].lc==y)
 zip(x),zap(x);
 else zap(x),zip(x);
 }
 }
 int find(int k)
 {
 int p=root;
 while()
 {
 push_down(p);
 if(tree[tree[p].lc].size>=k)
 p=tree[p].lc;
 else
 {
 k-=tree[tree[p].lc].size;
 if(k==) return p;
 k-=;
 p=tree[p].rc;
 }
 }
 }
 void reverse(int l,int r)
 {
 int L=find(l-);
 splay(L,root);
 int R=find(r+);
 splay(R,tree[L].rc);
 tree[tree[R].lc].mark^=;
 }
 void print(int x)
 {
 if(x==) return;
 push_down(x);
 print(tree[x].lc);
 if(tree[x].val!=INF&&tree[x].val!=-INF)
 {
 if(FIRST)
 {
 FIRST=;
 printf("%d",tree[x].val);
 }
 else printf(" %d",tree[x].val);
 }
 print(tree[x].rc);
 }

对了，顺便说一下，为什么我看的资料书里面，不同的平衡树的zip是不一样的？有些是表示左旋，有些是表示右旋，zap也是一样，导致我现在都是按照自己的标准来了。

我在CSDN也发了。https://blog.csdn.net/Liang_Si_FFF/article/details/84190616