POJ2187 Beauty Contest （旋转卡壳算法 求直径）

POJ2187

旋转卡壳算法如图

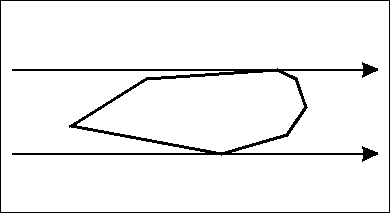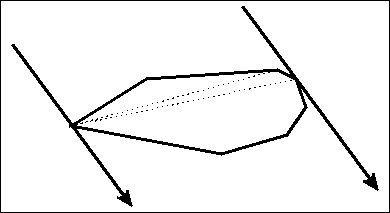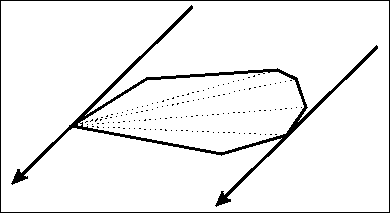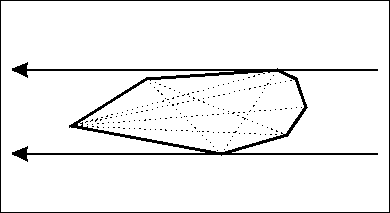
证明：对于直径AB 必然有某一时刻 A和B同时被卡住 所以旋转卡壳卡住的点集中必然存在直径

而卡壳过程显然是O（n）的 故可在O（n）时间内求出直径

凸包具有良好的性质 其中的点是有序的 对于某个点 从它之后的点与它的距离必然是一个单峰凸函数 根据这个性质也可以设计一个O（nlogn）的算法

给出代码

#include<iostream>
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
#include<math.h>
#include<algorithm>
#include<queue>
#include<vector>
using namespace std;

const double eps=1e-9;

int cmp(double x)
{
 if(fabs(x)<eps)return 0;
 if(x>0)return 1;
 	else return -1;
}

const double pi=acos(-1.0);

inline double sqr(double x)
{
 return x*x;
}

struct point
{
 double x,y;
 point (){}
 point (double a,double b):x(a),y(b){}
 void input()
 	{
 	 scanf("%lf%lf",&x,&y);
	}
 friend point operator +(const point &a,const point &b)
 	{
 	 return point(a.x+b.x,a.y+b.y);
	}
 friend point operator -(const point &a,const point &b)
 	{
 	 return point(a.x-b.x,a.y-b.y);
	}
 friend bool operator ==(const point &a,const point &b)
 	{
 	 return cmp(a.x-b.x)==0&&cmp(a.y-b.y)==0;
	}
 friend point operator *(const point &a,const double &b)
 	{
 	 return point(a.x*b,a.y*b);
	}
 friend point operator*(const double &a,const point &b)
 	{
 	 return point(a*b.x,a*b.y);
	}
 friend point operator /(const point &a,const double &b)
 	{
 	 return point(a.x/b,a.y/b);
	}
 double norm()
 	{
 	 return sqr(x)+sqr(y);
	}
};

struct line
{
 point a,b;
 line(){};
 line(point x,point y):a(x),b(y)
 {

 }
};
double det(const point &a,const point &b)
{
 return a.x*b.y-a.y*b.x;
}

double dot(const point &a,const point &b)
{
 return a.x*b.x+a.y*b.y;
}

double dist(const point &a,const point &b)
{
 return (a-b).norm();
}

point rotate_point(const point &p,double A)
{
 double tx=p.x,ty=p.y;
 return point(tx*cos(A)-ty*sin(A),tx*sin(A)+ty*cos(A));
}

bool parallel(line a,line b)
{
 return !cmp(det(a.a-a.b,b.a-b.b));
}

bool line_joined(line a,line b,point &res)
{
 if(parallel(a,b))return false;
 double s1=det(a.a-b.a,b.b-b.a);
 double s2=det(a.b-b.a,b.b-b.a);
 res=(s1*a.b-s2*a.a)/(s1-s2);
 return true;
}

bool pointonSegment(point p,point s,point t)
{
 return cmp(det(p-s,t-s))==0&&cmp(dot(p-s,p-t))<=0;
}

void PointProjLine(const point p,const point s,const point t,point &cp)
{
 double r=dot((t-s),(p-s))/dot(t-s,t-s);
 cp=s+r*(t-s);
}

struct polygon_convex
{
 vector<point>P;
 polygon_convex(int Size=0)
 	{
 	 P.resize(Size);
	}
};

bool comp_less(const point &a,const point &b)
{
 return cmp(a.x-b.x)<0||cmp(a.x-b.x)==0&&cmp(a.y-b.y)<0;

}

polygon_convex convex_hull(vector<point> a)
{
 polygon_convex res(2*a.size()+5);
 sort(a.begin(),a.end(),comp_less);
 a.erase(unique(a.begin(),a.end()),a.end());//删去重复点
 int m=0;
 for(int i=0;i<a.size();i++)
 	{
 	 while(m>1&&cmp(det(res.P[m-1]-res.P[m-2],a[i]-res.P[m-2]))<=0)--m;
 	 res.P[m++]=a[i];
	}
 int k=m;
 for(int i=int(a.size())-2;i>=0;--i)
 	{
 	 while(m>k&&cmp(det(res.P[m-1]-res.P[m-2],a[i]-res.P[m-2]))<=0)--m;
 	 res.P[m++]=a[i];
	}
 res.P.resize(m);
 if(a.size()>1)res.P.resize(m-1);
 return res;
}

bool is_convex(vector<point> &a)
{
 for(int i=0;i<a.size();i++)
 	{
 	 int i1=(i+1)%int(a.size());
 	 int i2=(i+2)%int(a.size());
 	 int i3=(i+3)%int(a.size());
 	 if((cmp(det(a[i1]-a[i],a[i2]-a[i1]))*cmp(det(a[i2]-a[i1],a[i3]-a[i2])))<0)
	  	return false;
	}
 return true;
}
int containO(const polygon_convex &a,const point &b)
{
 int n=a.P.size();
 point g=(a.P[0]+a.P[n/3]+a.P[2*n/3])/3.0;
 int l=0,r=n;
 while(l+1<r)
 	{
 	 int mid=(l+r)/2;
 	 if(cmp(det(a.P[l]-g,a.P[mid]-g))>0)
 	 	{
 	 	 if(cmp(det(a.P[l]-g,b-g))>=0&&cmp(det(a.P[mid]-g,b-g))<0)r=mid;
 	 	 	else l=mid;
		}else
			{
			 if(cmp(det(a.P[l]-g,b-g))<0&&cmp(det(a.P[mid]-g,b-g))>=0)l=mid;
 	 	 		else r=mid;
			}
	}
 r%=n;
 int z=cmp(det(a.P[r]-b,a.P[l]-b))-1;
 if(z==-2)return 1;
 return z;
}
long long int distant(point a,point b)
{
 return  (int(b.x)-int(a.x))*(int(b.x)-int(a.x))+(int(b.y)-int(a.y))*(int(b.y)-int(a.y));
}
double  convex_diameter(polygon_convex &a,int &First,int &Second)
{
 vector<point> &p=a.P;
 int n=p.size();
 double maxd=0;
 if(n==1)
 	{
 	 First=Second=0;
 	 return maxd;
	}
 #define next(i)((i+1)%n)
 for(int i=0,j=1;i<n;++i)
 	{
 	 while(cmp(det(p[next(i)]-p[i],p[j]-p[i])-det(p[next(i)]-p[i],p[next(j)]-p[i]))<0)
 	 	j=next(j);
 	 double d=dist(p[i],p[j]);
 	 if(d>maxd)
 	 	{
 	 	 maxd=d;
 	 	 First=i,Second=j;
		}
	 d=dist(p[next(i)],p[next(j)]);
	 if(d>maxd)
	 	{
	 	 maxd=d;
 	 	 First=next(i),Second=next(j);
		}

	}
 return maxd;
}

vector<point> pp;

int main()
{freopen("t.txt","r",stdin);
 pp.clear();
 int n;
 scanf("%d",&n);
 for(int i=0;i<n;i++)
 	{
 	 point pn;pn.input();
 	 pp.push_back(pn);
	}
 int a,b;
 polygon_convex pc= convex_hull(pp);
 int ans=0;

 printf("%.0lf\n",convex_diameter(pc,a,b));
 return 0;
}