cf575A Fibonotci

Fibonotci sequence is an integer recursive sequence defined by the recurrence relation

F_n = s_n - 1·F_n - 1 + s_n - 2·F_n - 2withF₀ = 0, F₁ = 1

Sequence s is an infinite and almost cyclic sequence with a cycle of length N. A sequence s is called almost cyclic with a cycle of length N if 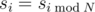, for i ≥ N, except for a finite number of values s_i, for which 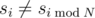(i ≥ N).

Following is an example of an almost cyclic sequence with a cycle of length 4:

s = (5,3,8,11,5,3,7,11,5,3,8,11,…)

Notice that the only value of s for which the equality 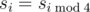does not hold is s₆ (s₆ = 7 and s₂ = 8). You are given s₀, s₁, ...s_N - 1 and all the values of sequence s for which 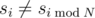(i ≥ N).

Find .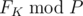

Input

The first line contains two numbers K and P. The second line contains a single number N. The third line contains N numbers separated by spaces, that represent the first N numbers of the sequence s. The fourth line contains a single number M, the number of values of sequence s for which 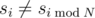. Each of the following M lines contains two numbers j and v, indicating that 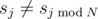and s_j = v. All j-s are distinct.

• 1 ≤ N, M ≤ 50000
• 0 ≤ K ≤ 10¹⁸
• 1 ≤ P ≤ 10⁹
• 1 ≤ s_i ≤ 10⁹, for all i = 0, 1, ...N - 1
• N ≤ j ≤ 10¹⁸
• 1 ≤ v ≤ 10⁹
• All values are integers

Output

Output should contain a single integer equal to .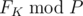

Examples

Input

10 8
3
1 2 1
2
7 3
5 4

Output

4

感觉是递推神题……f[n]=s[n-1]*f[n-1]+s[n-2]*f[n-2]，而且{s[i]}是个T=5w的循环数列，而且还换掉了s[i]当中5w个点……

先不考虑几个s[i]的特殊点

都算到f[1e18]了肯定是要用到矩阵快速幂了

构建矩阵比较简单：

f[n]   f[n-1]        *         s[n]     1           =             f[n+1]      f[n]

0        0                     s[n-1]    0                             0          0

那么

f[1]   f[0]        *            s[1]     1        *      s[2]      1       *  .....  *    s[n-1]     1         =         f[n]      f[n-1]

0        0                      s[0]    0                s[1]      0                        s[n-2]    0                      0          0

然后注意到s[i]是个循环的

所以就是算出一个循环内的转移矩阵的乘积，一个循环是

s[1]     1          ~          s[T]       1

s[0]     0                      s[T-1]    0

接下来直接快速幂即可。

然后考虑挖点的情况：对于一个s[k]的修改，实际上有两个矩阵受到了它的影响：

s[k]      1      和            s[k+1]   1

s[k-1]   0                     s[k]       0

所以每个修改拆成2个对矩阵里头的值的修改。这样就是对矩阵的单点修改不超过10w个

所有s[k]的修改按照k排个序

然后维护一个线段树，保存一个周期内的矩阵的乘积（对你没看错，线段树存的是矩阵）

每次同一个周期内的修改就直接在线段树上单点修改，做完之后ans乘个当前1到T的区间积，然后再单点改回去，下个周期再改。这样每个修改就是logT的

改回去的时候搞个栈就好了

最后输出个答案矩阵的左上角

 #include<cstdio>
 #include<iostream>
 #include<cstring>
 #include<cstdlib>
 #include<algorithm>
 #include<cmath>
 #include<queue>
 #include<deque>
 #include<set>
 #include<map>
 #include<ctime>
 #define LL long long
 #define inf 0x7ffffff
 #define pa pair<int,int>
 #define mkp(a,b) make_pair(a,b)
 #define pi 3.1415926535897932384626433832795028841971
 using namespace std;
 inline LL read()
 {
     LL x=,f=;char ch=getchar();
     while(ch<''||ch>''){if(ch=='-')f=-;ch=getchar();}
     while(ch>=''&&ch<=''){x=x*+ch-'';ch=getchar();}
     return x*f;
 }
 LL k,mod,T,C,cnt;
 LL s[];
 struct matrix{
     LL a[][];
     inline void init(){a[][]=a[][]=a[][]=a[][]=;}
     matrix operator *(matrix b)
     {
         matrix ans;ans.init();
         for (int k=;k<=;k++)
             for (int i=;i<=;i++)
                 for (int j=;j<=;j++)
                     ans.a[i][j]=(ans.a[i][j]+a[i][k]*b.a[k][j])%mod;
         return ans;
     }
 }ans;
 inline matrix getm(LL x)
 {
     matrix c;
     c.a[][]=s[x];c.a[][]=;c.a[][]=s[x-];c.a[][]=;
     return c;
 }
 struct segtree{
     int l,r;
     matrix m;
 }t[];
 int zhan[],top;
 inline void update(int k){t[k].m=t[k<<].m*t[k<<|].m;}
 inline void buildtree(int now,int l,int r)
 {
     t[now].l=l;t[now].r=r;
     if (l==r)
     {
         t[now].m=getm(l);
         return;
     }
     int mid=(l+r)>>;
     buildtree(now<<,l,mid);
     buildtree(now<<|,mid+,r);
     update(now);
 }
 inline void change(int now,int x,matrix m)
 {
     int l=t[now].l,r=t[now].r;
     if (l==r){t[now].m=m;return;}
     int mid=(l+r)>>;
     if (x<=mid)change(now<<,x,m);
     else change(now<<|,x,m);
     update(now);
 }
 inline matrix ask(int now,int x,int y)
 {
     int l=t[now].l,r=t[now].r;
     if (l==x&&r==y)return t[now].m;
     int mid=(l+r)>>;
     if (y<=mid)return ask(now<<,x,y);
     else if (x>mid)return ask(now<<|,x,y);
     else return ask(now<<,x,mid)*ask(now<<|,mid+,y);
 }
 inline matrix quickpow(matrix a,LL b)
 {
     matrix s;s.init();s.a[][]=s.a[][]=;
     while (b)
     {
         if (b&)s=s*a;
         a=a*a;
         b>>=;
     }
     return s;
 }
 struct cg{LL pos,rnk,x,op;}c[],lst;
 bool operator <(cg a,cg b){return a.rnk<b.rnk||a.rnk==b.rnk&&a.pos<b.pos;}
 bool operator <=(cg a,cg b){return !(b<a);}
 int main()
 {
     k=read();mod=read();T=read();
     if (k==){puts("");return ;}
     if (k==){printf("%d\n",%mod);return ;}
     k--;lst.rnk=k/T+(k%T!=);lst.pos=k%T;if (!lst.pos)lst.pos=T;
     for (int i=;i<T;i++)s[i]=read();s[T]=s[];
     C=read();
     for (int i=;i<=C;i++)
     {
         LL a=read(),b=read();
         c[++cnt].rnk=a/T+(a%T!=);
         c[cnt].pos=a%T;if (!c[cnt].pos)c[cnt].pos=T;
         c[cnt].x=b;c[cnt].op=;

         c[++cnt].rnk=a/T+;
         c[cnt].pos=a%T+;
         c[cnt].x=b;c[cnt].op=;
     }
     sort(c+,c+cnt+);
     buildtree(,,T);
     ans.a[][]=;
     LL now2=;
     for (int i=;i<=cnt;i++)
     {
         if(c[i]<=lst)
         {
             if (c[i].rnk-!=now2)
             {
                 ans=ans*ask(,,T);
                 while (top){change(,zhan[top],getm(zhan[top]));top--;}
                 now2++;
                 if(now2!=c[i].rnk-)ans=ans*quickpow(ask(,,T),c[i].rnk--now2),now2=c[i].rnk-;
             }
             matrix chg=ask(,c[i].pos,c[i].pos);
             if (c[i].op==)chg.a[][]=c[i].x;else chg.a[][]=c[i].x;
             change(,c[i].pos,chg);
             zhan[++top]=c[i].pos;
         }else
         {
             if (now2<lst.rnk-)
             {
                 ans=ans*ask(,,T);
                 while (top){change(,zhan[top],getm(zhan[top]));top--;}
                 now2++;
                 if (now2<lst.rnk-)ans=ans*quickpow(ask(,,T),lst.rnk--now2);
             }
             ans=ans*ask(,,lst.pos);
             printf("%lld\n",ans.a[][]);return ;
         }
     }
     if (now2<lst.rnk-)
     {
         ans=ans*ask(,,T);
         while (top){change(,zhan[top],getm(zhan[top]));top--;}
         now2++;
         if (now2<lst.rnk-)ans=ans*quickpow(ask(,,T),lst.rnk--now2);
     }
     ans=ans*ask(,,lst.pos);
     printf("%lld\n",ans.a[][]);return ;
 }

cf 575A