51nod 1379 索函数

Fib[0]=0,Fib[1]=1,Fib[n]=Fib[n-1]+Fib[n-2] if n>1.

定义索函数Sor(n)=Fib[0]| Fib[1] |Fib[2]|…|Fib[n].

给定整数n，要求计算Sor(n)%1,000,000,007(1e9+7).

Input

第1行：给出一个整数T，表示有T组数据。(1<=T<=10000)
第2行到T+1行，每行一个整数n。(0<=n<=10^10)

Output

对于每个测试用例，输出结果占一行。

Input示例

2
1
2

Output示例

1
1

思路：
　　因为是或运算，那么将其Sor(n)转化为二进制，每一位上的值均应该为1，那么我们只需要求出二进制的位长，便可以求得Sor(n)。
　　对于斐波那契数列数列有： 

　　　

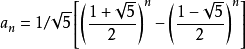
　　此时求其以2为底的对数，无法去掉n次幂，很难进行进一步化简，我们继续考虑：

　　当n趋近于无穷大时:

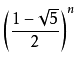　　的值趋近于0，

　　即此时求出Sor(n)转化为二进制时的长度为：

log2(15√(1+5√2)n)

log2(15√(1+5√2)n)

　　　

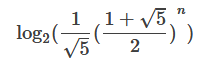
　　进行化简得：

　　

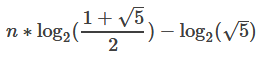
　　可以O(1)求出Sor(n)的位长len，通过快速幂求出 2^(len+1)的值后减去一得到Sor(n)的数值。

　　蛮有意思的一道题目。

　　

#include <stdio.h>
#include <math.h>
#define MAXSIZE 90
#define INF 0x3f3f3f3f
#define LL long long

const int mod = 1e9+;

double f[MAXSIZE];

LL Pow(LL a,LL n)
{
    LL ans = ;
    while(n)
    {
        if(n & )
        {
            ans = (ans*a)%mod;
        }
        a = (a*a)%mod;
        n >>= ;
    }
    return ans%mod;
}

LL Solve(LL n)
{
    LL ans,len;
    if(n < MAXSIZE)
    {
        len = log(f[n])/log(2.0);
    }
    else
        len = n*log((+sqrt(5.0))/2.0)/log(2.0) - log(sqrt(5.0))/log(2.0);
    ans = Pow(,len+);
    return ans;
}

int main()
{
    f[] = ;
    f[] = ;
    f[] = ;
    for(int i=;i<MAXSIZE;i++)
    {
        f[i] = f[i-] + f[i-];
    }
    int T;
    LL n;
    scanf("%d",&T);
    while(T--)
    {
        scanf("%lld",&n);
        if(n==)
        {
            printf("0\n");
            continue;
        }
        LL ans = Solve(n);
        printf("%lld\n",ans-);
    }
    return ;
}