pytorch学习-AUTOGRAD: AUTOMATIC DIFFERENTIATION自动微分

参考：https://pytorch.org/tutorials/beginner/blitz/autograd_tutorial.html#sphx-glr-beginner-blitz-autograd-tutorial-py

AUTOGRAD: AUTOMATIC DIFFERENTIATION

PyTorch中所有神经网络的核心是autograd包。让我们先简单地看一下这个，然后我们来训练我们的第一个神经网络。
autograd包为张量上的所有操作提供自动微分。它是一个按运行定义的框架，这意味着的、该支持是由代码的运行方式定义的，并且每个迭代都可以是不同的。

让我们用更简单的术语和一些例子来看看。

Tensor

torch.Tensor是包的中心类。如果将其属性.requires_grad设置为True，它将开始跟踪其上的所有操作。当你完成计算时，你可以调用 .backward()函数并自动计算所有的梯度。这个张量的梯度将累积为.grad属性。

要阻止张量跟踪历史，可以调用.detach()将其从计算历史中分离出来，并防止跟踪未来的计算。

为了防止跟踪历史(和使用内存)，还可以使用torch.no_grad():将代码块封装起来。这在评估模型时特别有用，因为模型可能有requires_grad=True的可训练参数，但我们不需要梯度。

还有一个类对autograd实现非常重要—— 即函数。

张量和函数是相互联系的，并建立一个无环图，它编码了一个完整的计算历史。每个张量都有一个.grad_fn属性，该属性引用一个创建了张量的函数(用户创建的张量除外 —— 它们的grad_fn为None)。

如果你想计算导数，你可以在一个张量上调用 .backward() 。如果张量是一个标量(即它包含一个元素数据)，你不需要指定任何参数给 .backward() ，但是如果它有更多的元素，你需要指定一个梯度参数，这是一个匹配形状的张量。

import torch

创建一个tensor x并设置requires_grad=True去追踪其计算；然后进行加法操作得到y， 这时候就能够查看y的.grad_fn属性去得到其计算的说明：

#-*- coding: utf- -*-
from __future__ import print_function
import torch

x = torch.ones(, , requires_grad=True)
print(x)

y = x +
print(y)

print(y.grad_fn)

返回：

(deeplearning) userdeMBP:pytorch user$ python test.py
tensor([[., .],
        [., .]], requires_grad=True)
tensor([[., .],
        [., .]], grad_fn=<AddBackward0>)
<AddBackward0 object at 0x101816358>

上面的最后的返回结果AddBackward0说明了该y是经过加法操作获得的

还可以进行更多的操作：

#-*- coding: utf- -*-
from __future__ import print_function
import torch

x = torch.ones(, , requires_grad=True)

y = x + 

z = y * y *
out = z.mean()

print(z)
print(out)

返回：

(deeplearning) userdeMBP:pytorch user$ python test.py
tensor([[., .],
        [., .]], grad_fn=<MulBackward0>)
tensor(., grad_fn=<MeanBackward1>)

可以看出来z是乘法操作得出的，out是求平均值操作得出的

.requires_grad_( ... )函数会改变现存的Tensor的内置requires_grad标签。如果没设置，这个标签默认为False，即不计算梯度

#-*- coding: utf- -*-
from __future__ import print_function
import torch

a = torch.randn(, )
a = ((a * ) / (a - ))
print(a)
print(a.requires_grad)

a.requires_grad_(True)
print(a)
print(a.requires_grad)

b = (a * a).sum()
print(b)
print(b.grad_fn)

返回：

(deeplearning) userdeMBP:pytorch user$ python test.py
tensor([[20.8490, -1.7316],
        [ 1.4831, -2.8223]])
False
tensor([[20.8490, -1.7316],
        [ 1.4831, -2.8223]], requires_grad=True)
True
tensor(447.8450, grad_fn=<SumBackward0>)
<SumBackward0 object at 0x10c381400>

Gradients梯度

因为out中只包含了一个标量，out.backward()和out.backward(torch.tensor(1.))的值是相同的

#-*- coding: utf- -*-
from __future__ import print_function
import torch

x = torch.ones(, , requires_grad=True)

y = x + 

z = y * y *
out = z.mean()

print(out)
out.backward()
print(x.grad) # 得到out相对于x的梯度d(out)/dx

返回：

(deeplearning) userdeMBP:pytorch user$ python test.py
tensor(., grad_fn=<MeanBackward1>)
tensor([[4.5000, 4.5000],
        [4.5000, 4.5000]])

省略计算步骤

你应该得到值为4.5的矩阵。让我们将out称为Tensor "o"。o的计算公式为o=1/4 ∑_iz_i，z_i=3(x_i+2)²且 zi∣xi=1=27。因此o对x_i求导为 ∂_o/∂_xi=3/2(x_i+2), 带入x_i=1，则得到值4.5.

数学上，如果你有一个向量值函数 y⃗ =f(x⃗），那么 y⃗相对于 x⃗的梯度就是一个Jacobian矩阵：

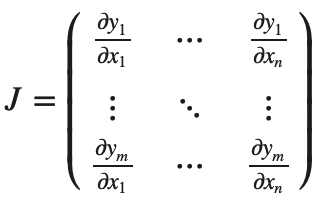
一般来说,torch.autograd是一个计算vector-Jacobian矩阵乘积的引擎。也就是说，给定任意向量v=(v₁v₂⋯v_m)^T,计算v^T⋅J。

如果v是一个标量函数 l=g(y⃗）的梯度，那么v为 v=(∂l/∂y₁⋯∂l/∂y_m)^T,根据链式法则，vector-Jacobian矩阵乘积就是l相对与x的梯度: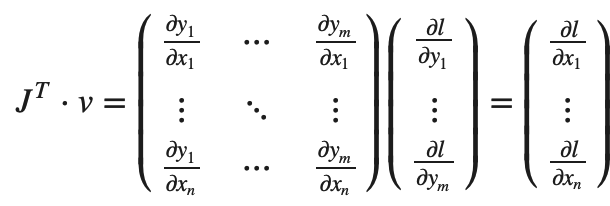

⚠️v^T⋅J给出一个行向量，通过 J^T⋅v该行向量可以被视为列向量

vector-Jacobian矩阵乘积的这种特性使得将外部梯度输入具有非标量输出的模型变得非常方便。
现在让我们看一个vector-Jacobian矩阵乘积的例子:

#-*- coding: utf- -*-
from __future__ import print_function
import torch

x = torch.randn(, requires_grad=True)
print(x)
y = x *
print(y)
while y.data.norm() < : #归一化
    y = y * 

print(y)

返回：

(deeplearning) userdeMBP:pytorch user$ python test.py
tensor([0.6542, 0.1118, 0.1979], requires_grad=True)
tensor([1.3084, 0.2236, 0.3958], grad_fn=<MulBackward0>)
tensor([1339.8406,  229.0077,  405.2867], grad_fn=<MulBackward0>)

在这种情况下，y不再是标量。 torch.autograd不能直接计算出整个Jacobian矩阵，但是如果我们只想要vector-Jacobian矩阵乘积，只需将向量作为参数向后传递:

#-*- coding: utf- -*-
from __future__ import print_function
import torch

x = torch.randn(, requires_grad=True)
print(x)
y = x *
print(y)
while y.data.norm() < : #归一化
    y = y * 

v = torch.tensor([0.1, 1.0, 0.0001], dtype=torch.float)
y.backward(v)

print(x.grad)

返回：

(deeplearning) userdeMBP:pytorch user$ python test.py
tensor([-0.7163,  1.6850, -0.0286], requires_grad=True)
tensor([-1.4325,  3.3700, -0.0572], grad_fn=<MulBackward0>)
tensor([1.0240e+02, 1.0240e+03, 1.0240e-01])

你可以通过使用with torch.no_grad():来封装代码块去阻止带有.requires_grad=True配置的Tensors的autograd去追踪历史：

#-*- coding: utf- -*-
from __future__ import print_function
import torch

x = torch.randn(, requires_grad=True)

print(x.requires_grad)
print((x ** ).requires_grad)

with torch.no_grad():
    print((x ** ).requires_grad)

返回：

(deeplearning) userdeMBP:pytorch user$ python test.py
True
True
False

有关autograd和Function的文档可见https://pytorch.org/docs/autograd