UVA1646-Edge Case（递推+斐波那契数列）

Problem UVA1646-Edge Case

Time Limit: 3000 mSec

Problem Description

Input

For each test case, you get a single line containing one positive integer: n, with 3 ≤ n ≤ 10000.

 Output

For each test case, a row containing the number of matchings in Cn.

 

 Sample Input

3

4

100

Sample Output

4
7
792070839848372253127

题解：这个题一看样例就知道涉及高精度，不过只有加法，即便用C++写也没有什么难度，大致看了一下网上的题解，都是只说找规律没有证明（可能是我没翻到），因此在这里简单做个说明。

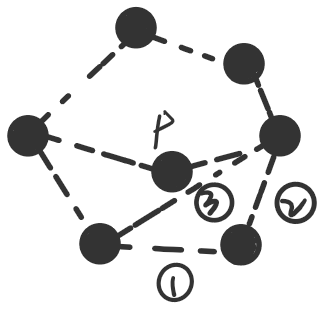
首先设最终结果为a[n]，递推过程中需要引入一个中间序列b[n]，b[n]的含义是强制让1、2两条边不连的匹配数。由此我们得到第一个递推式：

a[n] = b[n] + 2*b[n-1]

解释一下，n的时候的所有成立的情况可以分为三类，

1、1号边和2号边都不连

2、1号边连，2号边不连

3、2号边连，1号边不连

第一种情况自然对应b[n]，第二种情况，如果1连，则1的左右两条边都不能连，这时看我引入的点P以及它连出的线段，它们将多边形分成上下两部分，只看上半部分，第二种情况的情况数就等于上半部分多边形强制让点P连的线段不连的情况数，即b[n-1]，第三种情况类似。

我们再找一个关系式就可以递推了。从第一种情况入手，第一种情况等价于只有n-1个点时3号边不连，那我们就求强制让3不连的匹配数，发现不太好求，那就求强制让3连的匹配数，如果3号边连，那么它左右两条边都不能连，因此类似刚才的分析，匹配数等于b[n-1-1]=b[n-2]，这样一来得到如下关系式：

b[n] = a[n-1]-b[n-2]

有了这两个关系式，解出数列a即可，基本操作，不再赘述。

 #include <bits/stdc++.h>

 using namespace std;

 const int maxn =  + ;

 int Fib[maxn][];
 int n;

 void prepare()
 {
     Fib[][] = ;
     Fib[][] = ;
     Fib[][] = ;
     Fib[][] = ;
     for (int i = ; i < maxn; i++)
     {
         for (int j = ; j <= max(Fib[i - ][], Fib[i - ][]); j++)
         {
             Fib[i][j] += Fib[i - ][j] + Fib[i - ][j];
             Fib[i][j + ] = Fib[i][j] / ;
             Fib[i][j] %= ;
         }
         Fib[i][] = max(Fib[i - ][], Fib[i - ][]);
         if (Fib[i][Fib[i][] + ])
             Fib[i][]++;
     }
 }

 int main()
 {
     //freopen("input.txt", "r", stdin);
     //freopen("output.txt", "w", stdout);
     prepare();
     while (~scanf("%d", &n))
     {
         for (int i = Fib[n][]; i; i--)
             printf("%d", Fib[n][i]);
         printf("\n");
     }
     return ;
 }