机器学习笔记(5) KNN算法

这篇其实应该作为机器学习的第一篇笔记的,但是在刚开始学习的时候,我还没有用博客记录笔记的打算.所以也就想到哪写到哪了.

你在网上搜索机器学习系列文章的话,大部分都是以KNN（k nearest neighbors）作为第一篇入门的,因为这个算法实在是太简单了.简单到其实没啥可说的.

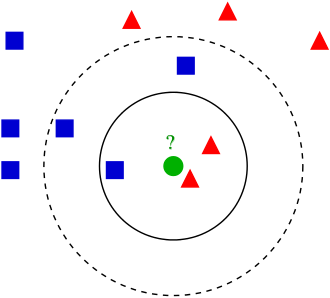
问题：已知正方形和三角形两种分类,现在来了个圆,问：应该归到正方形更合适还是三角形更合适？

算法的思想很朴素,假设我们有一个M*N的矩阵(M个样本,每个样本有N个特征).当我们来了一个新的样本test,我们要去判断这个样本属于什么类别,我们去计算test与M个样本中每一个样本的距离,选取最近的K个样本,投票出test的类别.

前面说了,通过判断两个样本之间的距离(或者说N维空间中的2个点之间的距离),来判断两个样本的相似程度. 那问题来了,我们如何表达"两个点之间的距离呢"？

二维空间中距离：$$\sqrt {(x^{(a)}-x^{(b)})^2+(y^{(a)}-y^{(b)})^2}$$

三维空间中距离：$$\sqrt {(x^{(a)}-x^{(b)})^2+(y^{(a)}-y^{(b)})^2+(z^{(a)}-z^{(b)})^2}$$

推而广之,N维空间中距离：$$\sqrt {(x_1^{(a)}-x_1^{(b)})^2+(x_2^{(a)}-x_2^{(b)})^2+…+(x_n^{(a)}-x_n^{(b)})^2} =\sqrt {\sum_{i=1}^n(x_i^{(a)}-x_i^{(b)})^2}$$

这就是我们熟知的欧拉距离.

实际上,如何度量距离,还有曼哈顿距离,$$\sum_{i=1}^n |X_i^{(a)}-X_i^{(b)}|$$

欧拉距离和曼哈顿距离都可以统一表达为明科夫斯基距离$$（\sum_{i=1}^n |X_i^{(a)}-X_i^{(b)}|^p）^\frac 1 p$$,

当p=1时,即是曼哈顿距离,当p=2时,即是欧拉距离.sklearn中默认的p=2.

事实上,距离的表达不仅仅是明科夫斯基距离,还有很多种,就不一一介绍了：

Metrics intended for real-valued vector spaces:

identifier	class name	args	distance function
“euclidean”	EuclideanDistance		sqrt(sum((x - y)^2))
“manhattan”	ManhattanDistance		sum(|x - y|)
“chebyshev”	ChebyshevDistance		max(|x - y|)
“minkowski”	MinkowskiDistance	p	sum(|x - y|^p)^(1/p)
“wminkowski”	WMinkowskiDistance	p, w	sum(|w * (x - y)|^p)^(1/p)
“seuclidean”	SEuclideanDistance	V	sqrt(sum((x - y)^2 / V))
“mahalanobis”	MahalanobisDistance	V or VI	sqrt((x - y)' V^-1 (x - y))

Metrics intended for integer-valued vector spaces: Though intended for integer-valued vectors, these are also valid metrics in the case of real-valued vectors.

identifier	class name	distance function
“hamming”	HammingDistance	N_unequal(x, y) / N_tot
“canberra”	CanberraDistance	sum(|x - y| / (|x| + |y|))
“braycurtis”	BrayCurtisDistance	sum(|x - y|) / (sum(|x|) + sum(|y|))

知道如何计算距离了,似乎我们的KNN已经可以工作了,但是,问题又来了,考虑一下这个场景：我们选取K=3，然鹅,好巧不巧的,最终算出来的最近的3个距离是一样的,而这3个样本又分别属于不同的类别,这我们要怎么归类呢？如果你觉得这个例子比较极端,那考虑一下这个场景：我们通过计算找出了距离待测样本最近的3个点,假设这3个点p1,p2,p3分别属于类别A，B，B. 但是,待测样本点距离点p1的距离为1,距离p2的距离为100，距离p3的距离为50.这个时候显然待测点和p1是极为接近的,把待测样本归类到A是更合理的.而由p1,p2,p3投票的话会把待测样本归类为B。

这就引入了权重(weight)的概念.由于p1和待测样本点距离极为接近,所以我们应该把p1的投票权重提高.

sklearn中的KNeighborsClassifier的weight参数有以下3个取值.

• ‘uniform’ : uniform weights. All points in each neighborhood are weighted equally.
• ‘distance’ : weight points by the inverse of their distance. in this case, closer neighbors of a query point will have a greater influence than neighbors which are further away.
• [callable] : a user-defined function which accepts an array of distances, and returns an array of the same shape containing the weights.

uniform 代表等权重. sklean中默认取值是uniform。

distance代表用距离的倒数作为权重.

callable代表用户自定义函数.

以下是sklearn中KNeighborsClassifier的具体参数.

class sklearn.neighbors.KNeighborsClassifier(n_neighbors=5, weights=’uniform’, algorithm=’auto’, leaf_size=30, p=2, metric=’minkowski’, metric_params=None, n_jobs=None, **kwargs)[source]¶

n_neighbors : int, optional (default = 5)

Number of neighbors to use by default for kneighbors queries.

weights : str or callable, optional (default = ‘uniform’)

weight function used in prediction. Possible values:

• ‘uniform’ : uniform weights. All points in each neighborhood are weighted equally.
• ‘distance’ : weight points by the inverse of their distance. in this case, closer neighbors of a query point will have a greater influence than neighbors which are further away.
• [callable] : a user-defined function which accepts an array of distances, and returns an array of the same shape containing the weights.

algorithm : {‘auto’, ‘ball_tree’, ‘kd_tree’, ‘brute’}, optional

Algorithm used to compute the nearest neighbors:

• ‘ball_tree’ will use BallTree
• ‘kd_tree’ will use KDTree
• ‘brute’ will use a brute-force search.
• ‘auto’ will attempt to decide the most appropriate algorithm based on the values passed to fitmethod.

Note: fitting on sparse input will override the setting of this parameter, using brute force.

leaf_size : int, optional (default = 30)

Leaf size passed to BallTree or KDTree. This can affect the speed of the construction and query, as well as the memory required to store the tree. The optimal value depends on the nature of the problem.

p : integer, optional (default = 2)

Power parameter for the Minkowski metric. When p = 1, this is equivalent to using manhattan_distance (l1), and euclidean_distance (l2) for p = 2. For arbitrary p, minkowski_distance (l_p) is used.

metric : string or callable, default ‘minkowski’

the distance metric to use for the tree. The default metric is minkowski, and with p=2 is equivalent to the standard Euclidean metric. See the documentation of the DistanceMetric class for a list of available metrics.

metric_params : dict, optional (default = None)

Additional keyword arguments for the metric function.

n_jobs : int or None, optional (default=None)

The number of parallel jobs to run for neighbors search. None means 1 unless in a joblib.parallel_backend context. -1 means using all processors. See Glossary for more details. Doesn’t affect fit method.

>>> X = [[0], [1], [2], [3]]
>>> y = [0, 0, 1, 1]
>>> from sklearn.neighbors import KNeighborsClassifier
>>> neigh = KNeighborsClassifier(n_neighbors=3)
>>> neigh.fit(X, y)
KNeighborsClassifier(...)
>>> print(neigh.predict([[1.1]]))
[0]
>>> print(neigh.predict_proba([[0.9]]))
[[0.66666667 0.33333333]]

---

到了这里,是不是觉得大功告成了呢？等等,还有问题...........

思考下这个场景：（一时间没有想出特别合适的例子,凑合看吧）

我们根据头发长度和指甲长度去判断一个人是男是女

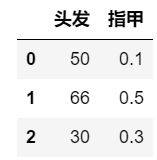
发现什么问题没有,两列数据的量级不在一个尺度上.所以在我们计算距离时,指甲长度的影响几乎可以忽略不计了.这显然不是我们想要的结果.

这里就引入了一个话题：数据的归一化.  数据归一化将所有的数据映射到同一尺度.

最值归一化，既用下面的公式把所有数据映射到0-1之间：

$$x_{scale} = \frac {x - x_{min}} {x_{max} - x_{min}}$$

最值归一化虽然简便，但是是有一定适用范围的，那就是适用于样本数据有明显分布边界的情况，并且最值归一化太容易受异常样本点的影响了,实际并不常用。

均值方差归一化，该方法就是把所有数据归一到均值为0方差为1的分布中，公式如下：

$$x_{scale} = \frac {x - x_{mean}} S$$

就是将每个值减去均值，然后除以方差，通过均值方差归一化后的数据不一定在0-1之间，但是他们的均值为0，方差为1。

关于两种归一化的适用场景,优缺点等请戳这里.

至此,KNN使用时需要注意的一些点也就写的差不多了,希望对大家有所启发.