Lingo求解线性规划案例4——下料问题

凯鲁嘎吉 - 博客园

http://www.cnblogs.com/kailugaji/

造纸厂接到定单，所需卷纸的宽度和长度如表

卷纸的宽度	长度
5 7 9	10000 30000 20000

工厂生产1号(宽度10)和2号(宽度20)两种标准卷纸，其长度未加规定。现按定单要求对标准卷纸进行切割，切割后有限长度的卷纸可连接起来达到所需卷纸的长度。问如何安排切割计划以满足定单需求而使切割损失最小?

解：为了满足定单要求和使切割损失最小，我们可以使用多种切割方法来进行组合。此时，我们不但要考虑对两种标准卷纸的宽度如何进行切割，而且还要确定按某一种方式切割时标准卷纸所耗用的长度。

例如，可以把宽10的1号标准卷纸切割成宽5的卷纸2卷，根据定单要求，此时需1号标准卷纸5000单位长度，与此同时，把宽度20的2号标准卷纸切割成宽度7和宽度9的卷纸各1卷，此时为满足定单要求，需2号标准卷纸30000单位长度。按此切割方案，宽度9的卷纸多生产10000单位长度，因此，切割损失的面积为(20-7-9) ×30000+9×10000。

设xij为第i号标准卷纸按第j种方式切割时所耗用的长度。

各种可能的切割方式及切割损失宽度由下表给出(每种方式所产生的切割损失宽度应小于5)。

                                            

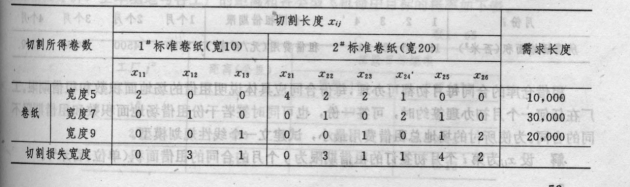
按这9种切割方式，宽度9的卷纸所得长度为

    x13+x23+x25+2x26。

令  xl=x13+x23+x25+2x26-20000，则宽度9、长度x1的卷纸再可切割成宽度5(切割损失宽度4)或宽度7(切割损失宽度2)的卷纸设它们的长度分别为x2及x3

现在切割所得宽度7的卷纸其长度为

    x12+x22+2x24+x25+x3

令    x4=x12+x22+2x24+x25+x3-30000，则宽度7、长度x4的卷纸又可切割成宽度5的卷纸(切割损失宽度2)。

在上述切割方式组合的条件下，宽度5的卷纸其所得长度为

    2xll+4x21+2x22+2x23+x24+x2+x4

令    x5=2x11+4x21+2x22+2x23+x24+x2+x4-10000

我们应注意到，4x2，2x3，2x4，5x5都为卷纸的切割损失面积。从而，总的切割损失面积

    f=3x12+x13+3x22+x23+x24+4x25+2x26+4x2+2x3+2x4+5x5

于是，我们得本问题的线性规划模型：

    minf=3x12+x13+3x22+x23+x24+4x25+2x26+4x2+2x3+2x4+5x5

 s．t． 2x11+4x21+2x22+2x23+x24+x2+x4- x5=10000

             x12+x22+2x24+x25+x3- x4=30000

             x13+x23+x25+2x26- x1=20000

            x2+x3=x1，

            xlj≥0，  j=1，2，3

            x2j≥0，  j=1，…，6

            xj≥0，  j=1，…，5

Lingo程序：

min=3*x12+x13+3*x22+x23+x24+4*x25+2*x26+2*x3+5*x5+4*x2+2*x4;
2*x11+4*x21+2*x22+2*x23+x24+x2+x4-x5=10000;
x12+x22+2*x24+x25+x3-x4=30000;
x13+x23+x25+2*x26-x1=20000;
x2+x3=x1;
end

结果为：

Global optimal solution found.
  Objective value:                              60000.00
  Infeasibilities:                              0.000000
  Total solver iterations:                             1

                       Variable           Value        Reduced Cost
                            X12        0.000000            0.000000
                            X13        0.000000            0.000000
                            X22        0.000000            10.00000
                            X23        0.000000            10.00000
                            X24        10000.00            0.000000
                            X25        0.000000            0.000000
                            X26        15000.00            0.000000
                             X3        10000.00            0.000000
                             X5        0.000000            0.000000
                             X2        0.000000            10.00000
                             X4        0.000000            10.00000
                            X11        0.000000            10.00000
                            X21        0.000000            20.00000
                             X1        10000.00            0.000000

                            Row    Slack or Surplus      Dual Price
                              1        60000.00           -1.000000
                              2        0.000000            5.000000
                              3        0.000000           -3.000000
                              4        0.000000           -1.000000
                              5        0.000000            1.000000