Solution -「BZOJ3894」文理分科

Sol.

说实话，对于一个初学者，这道题很难看出是一道网络流-最小割。对于一个熟练者，这是比较套路的一种模型。

最小割，可以看做是在一个图中删掉最小的边权和使得源点、汇点不连通。或者换一个角度，可以看做是将图中的所有点以最小的代价分成两个阵营。

现在就有点像这道题了。我们以损失最小代价将这些学生分开为文理两阵营。

答案即为 \(\sum \limits _{i, j} \mathrm{Art}(i, j) + \sum \limits _{i, j} \mathrm{Science}(i, j) + \sum \limits _{i, j} \mathrm{SameArt}(i, j) + \sum \limits _{i, j} \mathrm{SameScience}(i, j) - d\)。

其中 \(d\) 就是我们要考虑的最小代价，可以根据上面的思路设想到它应该是一个流图的最小割。

研究以下这个图的一些限定条件，不妨设 \(S\) 为文阵营，即源点，\(T\) 为理阵营，即汇点。则有：

• 对于一个割，所有的图中表示人的结点应该与且仅与 \(S,T\) 中的一个连通。
• 当表示两个相邻的人的结点属于同一阵营时，一定有与它们属于另一阵营产生的额外价值等量的边（允许多条）属于割。
• 再发现，若一条边的边权为极值，则可以看做我们强制绑定了两点，且该边一定不出现在割中。

我很难描述具体构图时的思路。

大概是灵活运用极值边权，以及多考虑若一边属于割则会损失多少权值这样的小事件。

基础想法先是将 \(S\) 和一个人相连，边权为 \(\mathrm{Art}\)，再将该人与 \(T\) 相连，边权为 \(\mathrm{Science}\)。

对于一个人即它相邻的人，我们考虑加入两个虚点，到 \(S, T\) 分别连 \(\mathrm{SameArt}, \mathrm{SameScience}\)，再将这两个点和这五个人（当前人和相邻人）绑定。

也就是说如果这五人当中有一人与 \(S\) 连通，则连向 \(T\) 的虚点一定会断开。

如下图。（图源网络，侵删。

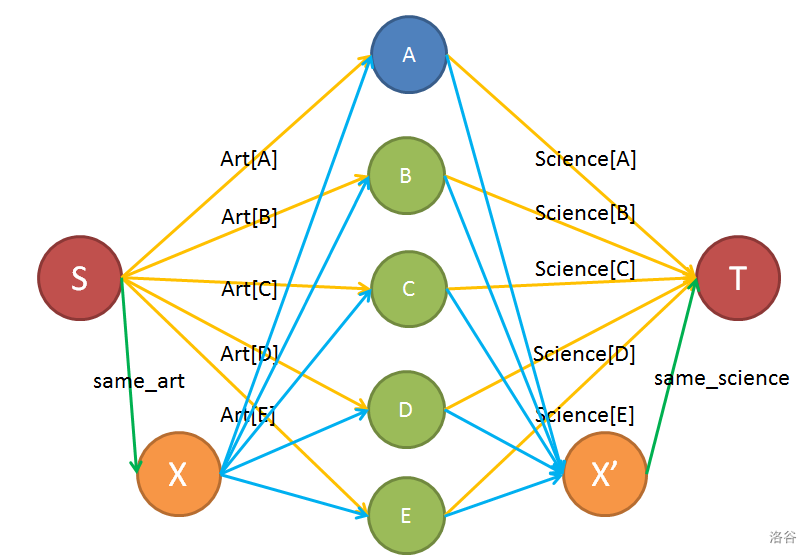
那么接下来就是一个最小割了。

---

Code.

#include <queue>
#include <cstdio>
using namespace std;
int Abs(int x) { return x < 0 ? -x : x; }
int Max(int x, int y) { return x > y ? x : y; }
int Min(int x, int y) { return x < y ? x : y; }
int read() {
    int x = 0, k = 1;
    char s = getchar();
    while(s < '0' || s > '9') {
        if(s == '-')
            k = -1;
        s = getchar();
    }
    while('0' <= s && s <= '9') {
        x = (x << 3) + (x << 1) + (s ^ 48);
        s = getchar();
    }
    return x * k;
}
void write(int x) {
    if(x < 0) {
        x = -x;
        putchar('-');
    }
    if(x > 9)
        write(x / 10);
    putchar(x % 10 + '0');
}
void print(int x, char s) {
    write(x);
    putchar(s);
}
const int MAXN = 1e2 + 5;
const int MAXM = 1e5 + 4e4 + 5;
const int MAXL = 3e4 + 5;
const int INF = 2147483647;
struct Maximum_flow {
    struct edge {
        int v, nxt;
        edge() {}
        edge(int V, int Nxt) {
            v = V, nxt = Nxt;
        }
    } e[MAXM << 1];
    int n, cnt, s, t;
    int Cap[MAXM << 1], Flow[MAXM << 1];
    int Lab[MAXL], Cur[MAXL], head[MAXL];
    queue<int> q;
    void init(int N, int S, int T) {
        for(int i = 0; i <= cnt; i++)
            Flow[i] = 0, Cap[i] = 0;
        n = N, cnt = 0, s = S, t = T;
        for(int i = 1; i <= n; i++)
            head[i] = -1;
    }
    void Add_Edge(int u, int v, int w) {
        Cap[cnt] += w;
        e[cnt] = edge(v, head[u]);
        head[u] = cnt++;
        e[cnt] = edge(u, head[v]);
        head[v] = cnt++;
    }
    bool Lab_Vertex() {
        for(int i = 1; i <= n; i++)
            Lab[i] = 0;
        Lab[t] = 1;
        while(!q.empty())
            q.pop();
        q.push(t);
        while(!q.empty()) {
            int v = q.front();
            q.pop();
            for(int i = head[v], u; ~i; i = e[i].nxt) {
                u = e[i].v;
                if(!Lab[u] && Cap[i ^ 1] - Flow[i ^ 1]) {
                    Lab[u] = Lab[v] + 1;
                    q.push(u);
                    if(u == s)
                        return Lab[s];
                }
            }
        }
        return Lab[s];
    }
    int Widen(int u, int Limit) {
        if(u == t)
            return Limit;
        int Used = 0, Delta;
        for(int i = Cur[u], v; ~i; i = e[i].nxt) {
            v = e[i].v;
            Cur[u] = i;
            if(Lab[v] + 1 != Lab[u] || Cap[i] - Flow[i] <= 0)
                continue;
            Delta = Widen(v, Min(Limit - Used, Cap[i] - Flow[i]));
            Used += Delta, Flow[i] += Delta, Flow[i ^ 1] -= Delta;
            if(Used == Limit)
                return Used;
        }
        return Used;
    }
    int Dinic() {
        int res = 0;
        while(Lab_Vertex()) {
            for(int i = 1; i <= n; i++)
                Cur[i] = head[i];
            res += Widen(s, INF);
            if(res < 0)
                return INF;
        }
        return res;
    }
} Flow_Graph;
int dir[5][2] = {{0, 0}, {0, 1}, {1, 0}, {-1, 0}, {0, -1}};
int a[MAXN][MAXN][2], s[MAXN][MAXN][2], n, m;
int Get(int x, int y) { return (x - 1) * m + y; }
int main() {
    n = read(), m = read();
    int Sum = 0;
    for(int i = 1; i <= n; i++)
        for(int j = 1; j <= m; j++)
            a[i][j][0] = read();
    for(int i = 1; i <= n; i++)
        for(int j = 1; j <= m; j++)
            s[i][j][0] = read();
    for(int i = 1; i <= n; i++)
        for(int j = 1; j <= m; j++)
            a[i][j][1] = read();
    for(int i = 1; i <= n; i++)
        for(int j = 1; j <= m; j++)
            s[i][j][1] = read();
    int S = n * m * 3 + 1, T = n * m * 3 + 2;
    Flow_Graph.init(T, S, T);
    for(int i = 1; i <= n; i++)
        for(int j = 1, Pos; j <= m; j++) {
            Pos = Get(i, j);
            Sum += a[i][j][0], Sum += a[i][j][1], Sum += s[i][j][0], Sum += s[i][j][1];
            Flow_Graph.Add_Edge(S, Pos, a[i][j][0]);
            Flow_Graph.Add_Edge(Pos, T, s[i][j][0]);
            Flow_Graph.Add_Edge(S, Pos + n * m, a[i][j][1]);
            Flow_Graph.Add_Edge(Pos + n * m * 2, T, s[i][j][1]);
            for(int k = 0, x, y; k < 5; k++) {
                x = i + dir[k][0], y = j + dir[k][1];
                if(x > n || x < 1 || y > m | y < 1)
                    continue;
                Flow_Graph.Add_Edge(Pos + n * m, Get(x, y), INF);
                Flow_Graph.Add_Edge(Get(x, y), Pos + n * m * 2, INF);
            }
        }
    print(Sum - Flow_Graph.Dinic(), '\n');
    return 0;
}