java实现二叉树的Node节点定义手撕8种遍历(一遍过)
java实现二叉树的Node节点定义手撕8种遍历(一遍过)
用java的思想和程序从最基本的怎么将一个int型的数组变成Node树状结构说起,再到递归前序遍历,递归中序遍历,递归后序遍历,非递归前序遍历,非递归前序遍历,非递归前序遍历,到最后的广度优先遍历和深度优先遍历
1.Node节点的Java实现
首先在可以看到打上Node这个字符串,就可以看到只能的IDEA系统提供的好多提示:
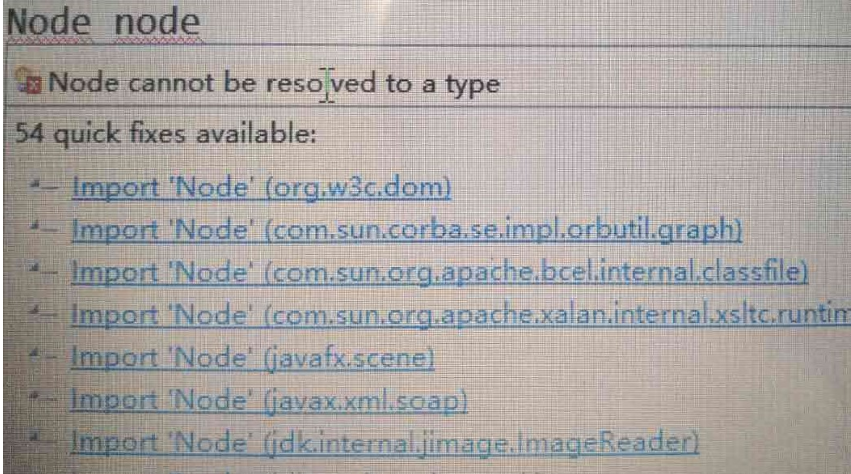
点进去看,却不是可以直接构成二叉树的Node,不是我们需要的东西。这里举个例子来看org.w3c.dom
这里面的Node是一个接口,是解析XML时的文档树。在官方文档里面看出:
该 Node 接口是整个文档对象模型的主要数据类型。它表示该文档树中的单个节点。
当实现 Node 接口的所有对象公开处理子节点的方法时,不是实现 Node 接口的所有对象都有子节点。
- 所以我们需要自定义一个Node类
package com.elloe.实现二叉树的Node节点.Node的Java实现;
import java.util.LinkedList;
import java.util.Stack;
/**
* @author ElloeStudy(Sifa Zhang)
* @create 2022-04-09 13:04
* To: 真常应物,真常得性,常清常静,常清静矣
*
* 自定义Node的节点
*/
public class Node {
private int value; // 节点的值
private Node node; // 当前节点
private Node left; // 此节点的左节点,类型为Node
private Node right; // 此节点的右节点,数据类型为Node
public Node() {
}
public Node(int value) {
this.value = value;
this.left = null;
this.right = null;
}
public int getValue() {
return value;
}
public void setValue(int value) {
this.value = value;
}
public Node getNode() {
return node;
}
public void setNode(Node node) {
this.node = node;
}
public Node getLeft() {
return left;
}
public void setLeft(Node left) {
this.left = left;
}
public Node getRight() {
return right;
}
public void setRight(Node right) {
this.right = right;
}
@Override
public String toString(){
return this.value + " ";
}
}
2.数组升华二叉树
一般拿到的数据是一个int型的数组,那怎么将这个数组变成我们可以直接操作的树结构呢?
1、数组元素变Node类型节点
2、给N/2-1个节点设置子节点
3、给最后一个节点设置子节点【有可能只有左节点】
那现在就直接上代码:
public static void create(int[] datas, List<Node> list){
// 将数组的数装换为节点Node
for (int i = 0; i < datas.length; i++) {
Node node = new Node(datas[i]);
node.setNode(node);
list.add(node);
}
// 节点关联树
for (int index = 0; index < list.size()/2 - 1; index++) {
//编号为n的节点他的左子节点编号为2*n 右子节点编号为2*n+1 但是因为list从0开始编号,所以还要+1
list.get(index).setLeft(list.get(index * 2 + 1));
list.get(index).setRight(list.get(index * 2 + 2));
}
// 单独处理最后一个节点,list.size()/2 -1 进行设置,避免单孩子情况
int index = list.size()/2 - 1;
list.get(index).setLeft(list.get(index * 2 + 1));
if (list.size()%2 == 1){
// 如果有奇数个节点,最后一个节点才有右节点
list.get(index).setRight(list.get(index * 2 + 2));
}
}
很细致的加上了很多的注释啊,所以保证一看就懂。
3.递归前序遍历
具体的原理没有什么好讲的,知道顺序即可
先序遍历过程:
(1)访问根节点;
(2)采用先序递归遍历左子树;
(3)采用先序递归遍历右子树;
这里用图来说明:
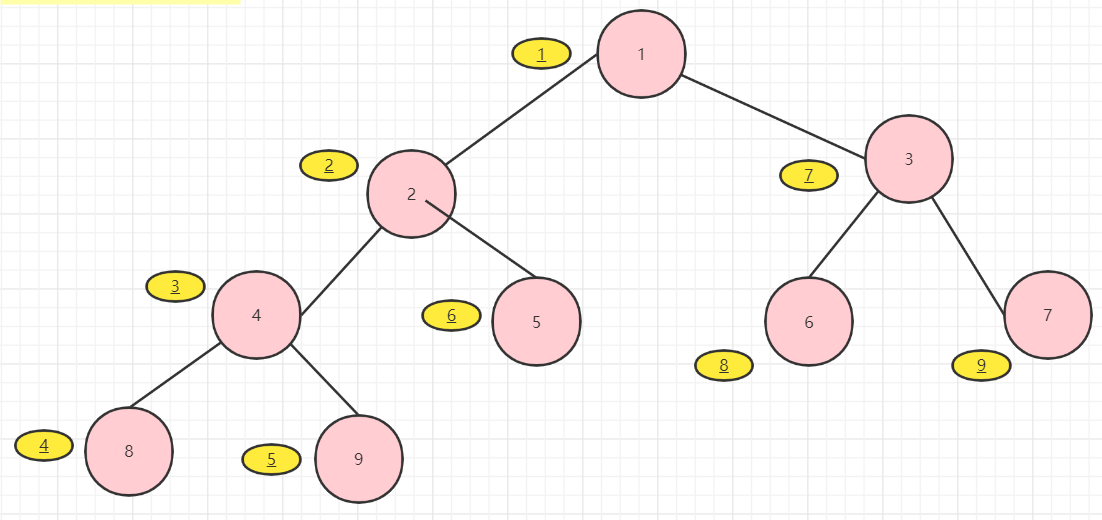
先序的结果:1 2 4 8 9 5 3 6 7
代码实现:
// 传入需要遍历的节点
public void preTraversal(Node node){
// 当遇到叶节点,停止向下遍历
if (node == null){
return;
}
// 相当于点前节点的根节点的值
System.out.print(node.getValue() + " ");
// 先从底下依次遍历左节点
preTraversal(node.getLeft());
// 先从底下依次遍历右节点
preTraversal(node.getRight());
}
看,说了很简单的!
4.递归中序遍历
中序遍历:
(1)采用中序遍历左子树;
(2)访问根节点;
(3)采用中序遍历右子树
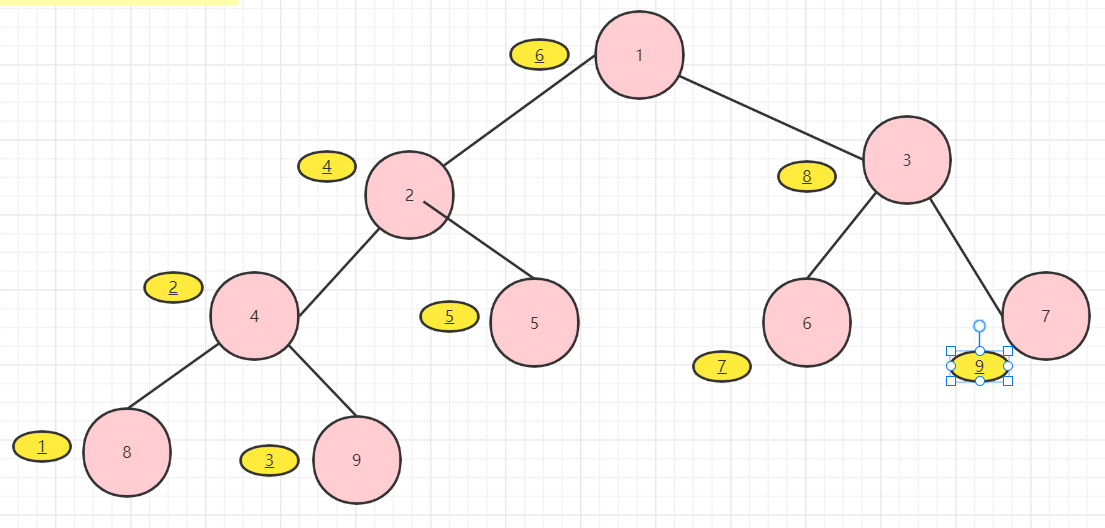
中序的结果:8 4 9 2 5 1 6 3 7
代码实现:
// 中序遍历(递归)
public void MidTraversal(Node node){
// 判断当前节点是否为叶子节点,如果为叶子节点,停止遍历
if (node == null){
return;
}
// 获得左节点
MidTraversal(node.getLeft());
// 获得根节点
System.out.print(node.getValue() + " ");
// 获得右节点
MidTraversal(node.getRight());
}
5.递归后序遍历
后序遍历:
(1)采用后序递归遍历左子树;
(2)采用后序递归遍历右子树;
(3)访问根节点;
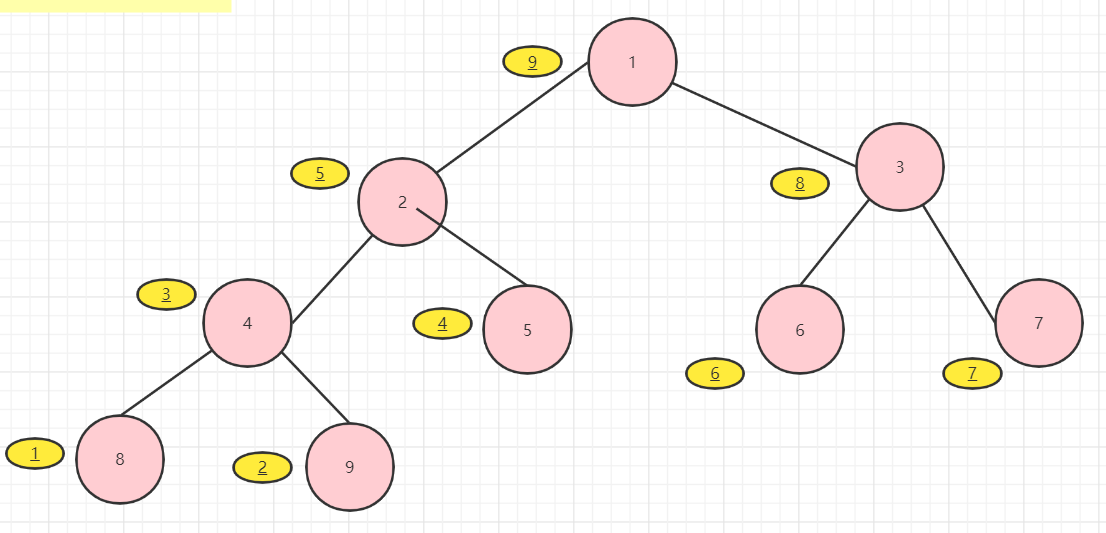
后序的结果:8 9 4 5 2 6 7 3 1
代码实现:
// 后序遍历(递归)
public void afterTraversal(Node node){
if (node == null){
return;
}
afterTraversal(node.getLeft());
afterTraversal(node.getRight());
System.out.print(node.getValue() + " ");
}
其实代码和思想一样,只是输出的位置和递归调用的位置不同而已。
个人觉得懂得非递归的原理和代码比懂递归更有意思,当你能手撕非递归二叉树遍历的时候,
面试官问你原理,还能不知道吗?
那接下来的三个模块就是非递归的三种遍历
拭目以待
6.非递归前序遍历
我这里使用了栈这个数据结构,用来保存不到遍历过但是没有遍历完全的父节点
之后再进行回滚。
基本的原理就是当循环中的present不为空时,就读取present的值,并不断更新present为其左子节点,
即不断读取左子节点,直到一个枝节到达最后的子节点,再继续返回上一层进行取值
代码:
// 非递归前序遍历
public void beforeTraversalByLoop(Node node){
// 创建栈保存遍历的节点,但又没有遍历完全的节点(即这个节点还没有操作完,临时保存一下)
Stack<Node> stack = new Stack<>();
Node present = node; // 当前的节点
while (present != null || !stack.isEmpty()){
// 当前的节点不为null 且 栈不为空
while (present != null){
// 当 当前的节点不为null时,读取present的值,
// 并不断更新present为其左子节点(不断读取左节点的值)
// 读取根节点
System.out.print(present.getValue() + " ");
stack.push(present); // 将present压入栈(此时这个节点还没有操作好,临时保存)
present = present.getLeft(); // 读取当前节点的左节点
}
if (!stack.isEmpty()){
// 当栈不为空时
present = stack.pop(); // 将临时保存的数取出
present = present.getRight(); // 操作临时保存的节点的右节点(此时左节点已经全部读取好了)
}
}
}
先序的结果:1 2 4 8 9 5 3 6 7
7.非递归中序遍历
同原理
就是当循环中的present不为空时,就读取present的值,并不断更新present为其左子节点,
但是切记这个时候不能进行输出,必须不断读取左子节点,直到一个枝节到达最后的子节点,
然后每次从栈中拿出一个元素,就进行输出,再继续返回上一层进行取值。
代码实现:
// 非递归中序遍历
public void traversalMidByLoop(Node node) {
// 创建栈保存遍历的节点,但又没有遍历完全的节点(即这个节点还没有操作完,临时保存一下)
Stack<Node> stack = new Stack<>();
Node present = node; // 当前操作的节点
while (present != null || !stack.isEmpty()) {
// 当前的节点不为null 且 栈不为空
// 获取左节点
while (present != null) {
stack.push(present);// 将present压入栈(此时这个节点还没有操作好,临时保存)
present = present.getLeft();// 读取当前节点的左节点
}
if (!stack.isEmpty()) {
present = stack.pop();
// 获取根节点
System.out.print(present.getValue() + " ");
present = present.getRight(); // 获取右节点
}
}
}
8.非递归后序遍历
后序遍历相比前面的前序遍历和中序遍历在编程这里会难一点,不过理解了思想,看代码还是没有什么问题的
代码实现:
// 非递归后序遍历
public void traversalAfterByLoop(Node node){
// 存放还没有完成操作的节点,临时储存
Stack<Node> stack = new Stack<>();
Node present = node; // 当前的操作节点
Node prev = node; // 先前的根节点(一个标志flag)
while (present != null || !stack.isEmpty()){
// 当前的节点不为null 且 栈不为空
while(present != null){
// 如果当前的节点不为空
stack.push(present); // 将当前这个节点临时存储
present = present.getLeft(); // 遍历获取其左节点
}
if (!stack.isEmpty()){
// 拿出栈顶的值,并没有进行删除
Node temp = stack.peek().getRight(); // 获取栈顶节点的右节点
// 节点没有右节点或者到达根节点【考虑到了最后一种情况】
if (temp == null || temp == prev){
present = stack.pop();
// 获取根节点
System.out.print(present.getValue() + " ");
prev = present; // 将当前的节点作为 根节点的标志(flag)
present = null; // 将当前节点 设为空
}else{
// 节点有右节点 或者 没有到达根节点
present = temp; // 将这个右节点设置为当前节点
}
}
}
}
最后就可以放大招了,来看看广度优先遍历和深度优先遍历吧
9.广度优先遍历
在广度优先遍历里面我用到了队列,不明白的小伙伴可以看我的上一篇!
// 广度优先遍历
public void bfs(Node root){
if (root == null) {
return ;
}
LinkedList<Node> queue = new LinkedList<>();
queue.offer(root); // 将根节点存入队列
//当队列里有值时,每次取出队首的node打印,打印之后判断node是否有子节点,
// 若有,则将子节点加入队列
while (queue.size() > 0){
Node node = queue.peek(); // 查看队列的头部节点,不会删除节点
queue.poll(); // 取出(移除)对首的节点并打印
System.out.print(node.getValue() + " ");
if (node.getLeft() != null){
// 如果有左节点,则将其存入队列
queue.offer(node.getLeft());
}
if (node.getRight() != null){
// 如果有右节点,则将其存入对列
queue.offer(node.getRight());
}
}
}
10.深度优先遍历
在深度优先遍历里面我用到了栈,不明白的小伙伴可以看我的上一篇!
// 深度优先遍历
public void dfs(Node root) {
if (root == null){
return;
}
Stack<Node> stack = new Stack<>();
stack.push(root); // 将根节点压入栈里面
while (!stack.isEmpty()){
Node node = stack.pop(); // 弹出栈顶的节点
System.out.print(node.getValue() + " ");
// 深度优先遍历,先遍历左边在右边,所以先将右边压入再将左边压入
if (node.getRight() != null){
stack.push(node.getRight());
}
if (node.getLeft() != null){
stack.push(node.getLeft());
}
}
}
11.测试用例(贴心吧)
public static void main(String[] args) {
int[] ints = new int[9];
for (int i = 0; i < ints.length; i++) {
ints[i] = i + 1;
}
List<Node> nodes = new ArrayList<>();
// 数组创建二叉树
BinaryFromArray.create(ints,nodes);
for (Node node : nodes){
System.out.print(node.getValue() + " ");
System.out.print(node.getNode() + " ");
System.out.print(node.getLeft() + " ");
System.out.println(node.getRight());
}
// 先序遍历(递归),从当前数组的第一个node节点开始
nodes.get(0).preTraversal(nodes.get(0));
// 中序遍历(递归),从当前数组的第一个node节点开始
System.out.print("\r\n"); // \r\n 换行
nodes.get(0).MidTraversal(nodes.get(0));
// 后序遍历(递归),从当前数组的第一个node节点开始
System.out.print("\r\n"); // \r\n 换行
nodes.get(0).afterTraversal(nodes.get(0));
}
public static void main(String[] args) {
int[] ints = new int[9];
for (int i = 0; i < ints.length; i++) {
ints[i] = i + 1;
}
List<Node> nodes = new ArrayList<>();
// 数组创建二叉树
BinaryFromArray.create(ints,nodes);
for (Node node : nodes){
System.out.print(node.getValue() + " ");
System.out.print(node.getNode() + " ");
System.out.print(node.getLeft() + " ");
System.out.println(node.getRight());
}
// 先序遍历,从当前数组的第一个node节点开始
nodes.get(0).beforeTraversalByLoop(nodes.get(0));
// 中序遍历,从当前数组的第一个node节点开始
System.out.println(" ");
nodes.get(0).traversalMidByLoop(nodes.get(0));
// 后序遍历,从当前数组的第一个node节点开始
System.out.println(" ");
nodes.get(0).traversalAfterByLoop(nodes.get(0));
}
public static void main(String[] args) {
int[] ints = new int[9];
for (int i = 0; i < ints.length; i++) {
ints[i] = i + 1;
}
List<Node> nodes = new ArrayList<>();
// 数组创建二叉树
BinaryFromArray.create(ints,nodes);
for (Node node : nodes){
System.out.print(node.getValue() + " ");
System.out.print(node.getNode() + " ");
System.out.print(node.getLeft() + " ");
System.out.println(node.getRight());
}
// 广度优先遍历
nodes.get(0).bfs(nodes.get(0));
// 深度优先遍历
System.out.println();
nodes.get(0).dfs(nodes.get(0));
}
12.全部代码(完整版)[前面成功的小伙伴可以直接跳过]
package com.elloe.实现二叉树的Node节点.Node的Java实现;
import java.util.LinkedList;
import java.util.List;
import java.util.Stack;
/**
* @author ElloeStudy(Sifa Zhang)
* @create 2022-04-09 13:04
* To: 真常应物,真常得性,常清常静,常清静矣
*
* 自定义Node的节点
*/
public class Node {
private int value; // 节点的值
private Node node; // 当前节点
private Node left; // 此节点的左节点,类型为Node
private Node right; // 此节点的右节点,数据类型为Node
public Node() {
}
public Node(int value) {
this.value = value;
this.left = null;
this.right = null;
}
public int getValue() {
return value;
}
public void setValue(int value) {
this.value = value;
}
public Node getNode() {
return node;
}
public void setNode(Node node) {
this.node = node;
}
public Node getLeft() {
return left;
}
public void setLeft(Node left) {
this.left = left;
}
public Node getRight() {
return right;
}
public void setRight(Node right) {
this.right = right;
}
@Override
public String toString(){
return this.value + " ";
}
// 构建二叉树
public static void create(int[] datas, List<Node> list){
// 将数组的数装换为节点Node
for (int i = 0; i < datas.length; i++) {
Node node = new Node(datas[i]);
node.setNode(node);
list.add(node);
}
// 节点关联树
for (int index = 0; index < list.size()/2 - 1; index++) {
//编号为n的节点他的左子节点编号为2*n 右子节点编号为2*n+1 但是因为list从0开始编号,所以还要+1
list.get(index).setLeft(list.get(index * 2 + 1));
list.get(index).setRight(list.get(index * 2 + 2));
}
// 单独处理最后一个节点,list.size()/2 -1 进行设置,避免单孩子情况
int index = list.size()/2 - 1;
list.get(index).setLeft(list.get(index * 2 + 1));
if (list.size()%2 == 1){
// 如果有奇数个节点,最后一个节点才有右节点
list.get(index).setRight(list.get(index * 2 + 2));
}
}
// 先序遍历(递归)
// 传入需要遍历的节点
public void preTraversal(Node node){
// 当遇到叶节点,停止向下遍历
if (node == null){
return;
}
// 相当于点前节点的根节点的值
System.out.print(node.getValue() + " ");
// 先从底下依次遍历左节点
preTraversal(node.getLeft());
// 先从底下依次遍历右节点
preTraversal(node.getRight());
}
// 中序遍历(递归)
public void MidTraversal(Node node){
// 判断当前节点是否为叶子节点,如果为叶子节点,停止遍历
if (node == null){
return;
}
// 获得左节点
MidTraversal(node.getLeft());
// 获得根节点
System.out.print(node.getValue() + " ");
// 获得右节点
MidTraversal(node.getRight());
}
// 后序遍历(递归)
public void afterTraversal(Node node){
if (node == null){
return;
}
afterTraversal(node.getLeft());
afterTraversal(node.getRight());
System.out.print(node.getValue() + " ");
}
// 非递归前序遍历
public void beforeTraversalByLoop(Node node){
// 创建栈保存遍历的节点,但又没有遍历完全的节点(即这个节点还没有操作完,临时保存一下)
Stack<Node> stack = new Stack<>();
Node present = node; // 当前的节点
while (present != null || !stack.isEmpty()){
// 当前的节点不为null 且 栈不为空
while (present != null){
// 当 当前的节点不为null时,读取present的值,
// 并不断更新present为其左子节点(不断读取左节点的值)
// 读取根节点
System.out.print(present.getValue() + " ");
stack.push(present); // 将present压入栈(此时这个节点还没有操作好,临时保存)
present = present.getLeft(); // 读取当前节点的左节点
}
if (!stack.isEmpty()){
// 当栈不为空时
present = stack.pop(); // 将临时保存的数取出
present = present.getRight(); // 操作临时保存的节点的右节点(此时左节点已经全部读取好了)
}
}
}
// 非递归中序遍历
public void traversalMidByLoop(Node node) {
// 创建栈保存遍历的节点,但又没有遍历完全的节点(即这个节点还没有操作完,临时保存一下)
Stack<Node> stack = new Stack<>();
Node present = node; // 当前操作的节点
while (present != null || !stack.isEmpty()) {
// 当前的节点不为null 且 栈不为空
// 获取左节点
while (present != null) {
stack.push(present);// 将present压入栈(此时这个节点还没有操作好,临时保存)
present = present.getLeft();// 读取当前节点的左节点
}
if (!stack.isEmpty()) {
present = stack.pop();
// 获取根节点
System.out.print(present.getValue() + " ");
present = present.getRight(); // 获取右节点
}
}
}
// 非递归后序遍历
public void traversalAfterByLoop(Node node){
// 存放还没有完成操作的节点,临时储存
Stack<Node> stack = new Stack<>();
Node present = node; // 当前的操作节点
Node prev = node; // 先前的根节点(一个标志flag)
while (present != null || !stack.isEmpty()){
// 当前的节点不为null 且 栈不为空
while(present != null){
// 如果当前的节点不为空
stack.push(present); // 将当前这个节点临时存储
present = present.getLeft(); // 遍历获取其左节点
}
if (!stack.isEmpty()){
// 拿出栈顶的值,并没有进行删除
Node temp = stack.peek().getRight(); // 获取栈顶节点的右节点
// 节点没有右节点或者到达根节点【考虑到了最后一种情况】
if (temp == null || temp == prev){
present = stack.pop();
// 获取根节点
System.out.print(present.getValue() + " ");
prev = present; // 将当前的节点作为 根节点的标志(flag)
present = null; // 将当前节点 设为空
}else{
// 节点有右节点 或者 没有到达根节点
present = temp; // 将这个右节点设置为当前节点
}
}
}
}
// 广度优先遍历
public void bfs(Node root){
if (root == null) {
return ;
}
LinkedList<Node> queue = new LinkedList<>();
queue.offer(root); // 将根节点存入队列
//当队列里有值时,每次取出队首的node打印,打印之后判断node是否有子节点,
// 若有,则将子节点加入队列
while (queue.size() > 0){
Node node = queue.peek(); // 查看队列的头部节点,不会删除节点
queue.poll(); // 取出(移除)对首的节点并打印
System.out.print(node.getValue() + " ");
if (node.getLeft() != null){
// 如果有左节点,则将其存入队列
queue.offer(node.getLeft());
}
if (node.getRight() != null){
// 如果有右节点,则将其存入对列
queue.offer(node.getRight());
}
}
}
// 深度优先遍历
public void dfs(Node root) {
if (root == null){
return;
}
Stack<Node> stack = new Stack<>();
stack.push(root); // 将根节点压入栈里面
while (!stack.isEmpty()){
Node node = stack.pop(); // 弹出栈顶的节点
System.out.print(node.getValue() + " ");
// 深度优先遍历,先遍历左边在右边,所以先将右边压入再将左边压入
if (node.getRight() != null){
stack.push(node.getRight());
}
if (node.getLeft() != null){
stack.push(node.getLeft());
}
}
}
}
13.小结
- 以上的代码,全部为我自己成功实现的coding,希望看到这里的你,已经完全理清二叉树的遍历
- 继续努力!!!
- 参考文章:https://blog.csdn.net/weixin_42636552/article/details/82973190

java实现二叉树的Node节点定义手撕8种遍历(一遍过)的更多相关文章
- Java实现二叉树的前序、中序、后序遍历(递归方法)
在数据结构中,二叉树是树中我们见得最多的,二叉查找树可以加速我们查找的效率,那么输出一个二叉树也变得尤为重要了. 二叉树的遍历方法分为三种,分别为前序遍历.中序遍历.后序遍历.下图即为一个二叉 ...
- Java实现二叉树的前序、中序、后序遍历(非递归方法)
在上一篇博客中,实现了Java中二叉树的三种遍历方式的递归实现,接下来,在此实现Java中非递归实现二叉树的前序.中序.后序遍历,在非递归实现中,借助了栈来帮助实现遍历.前序和中序比较类似,也简单 ...
- C语言递归实现二叉树(二叉链表)的三种遍历和销毁操作(实验)
今天写的是二叉树操作的实验,这个实验有三个部分: ①建立二叉树,采用二叉链表结构 ②先序.中序.后续遍历二叉树,输出节点值 ③销毁二叉树 二叉树的节点结构定义 typedef struct BiTNo ...
- 创建B树,动态添加节点,并使用三种遍历算法对树进行遍历
ks17:algorithm apple$ cat btree_test.c ///********************************************************** ...
- Java实现二叉树先序,中序,后序遍历
以下是我要解析的一个二叉树的模型形状 接下来废话不多直接上代码 一种是用递归的方法,另一种是用堆栈的方法: 首先创建一棵树: public class Node { private int data; ...
- 二叉树总结—建树和4种遍历方式(递归&&非递归)
版权声明:本文为博主原创文章,未经博主同意不得转载. https://blog.csdn.net/u013497151/article/details/27967155 今天总结一下二叉树.要考离散了 ...
- python、java实现二叉树,细说二叉树添加节点、深度优先(先序、中序、后续)遍历 、广度优先 遍历算法
数据结构可以说是编程的内功心法,掌握好数据结构真的非常重要.目前基本上流行的数据结构都是c和c++版本的,我最近在学习python,尝试着用python实现了二叉树的基本操作.写下一篇博文,总结一下, ...
- 算法进阶面试题05——树形dp解决步骤、返回最大搜索二叉子树的大小、二叉树最远两节点的距离、晚会最大活跃度、手撕缓存结构LRU
接着第四课的内容,加入部分第五课的内容,主要介绍树形dp和LRU 第一题: 给定一棵二叉树的头节点head,请返回最大搜索二叉子树的大小 二叉树的套路 统一处理逻辑:假设以每个节点为头的这棵树,他的最 ...
- Java实现二叉树的创建和遍历操作(有更新)
博主强烈建议跳过分割线前面的部分,直接看下文更新的那些即可. 最近在学习二叉树的相关知识,一开始真的是毫无头绪.本来学的是C++二叉树,但苦于编译器老是出故障,于是就转用Java来实现二叉树的操作.但 ...
随机推荐
- 5月4日 python学习总结 socketserver
一.socketserver SocketServer简化了网络服务器的编写. 它有4个类:TCPServer,UDPServer,UnixStreamServer,UnixDatagramServe ...
- 内网渗透----Linux信息收集整理
一.基础信息收集 1.查看系统类型 cat /etc/issue cat /etc/*-release cat /etc/lsb-release cat /etc/redhat-release 2.内 ...
- Docker安装与基本命令
docker安装 Ubuntu 更新apt包索引 sudo apt-get update 更新apt包索引 sudo apt-get upgrade 安装docker sudo apt-get ins ...
- [root-me](web-client)write up 一个大坑怎么填啊
root-me web-client writeup 地址:www.root-me.org HTML - disabled buttons 打开网页发现按钮不能按,查看源代码,有 'disabled' ...
- Ajax是什么?包含什么技术?有什么作用?
Ajax 是 Asynchronous JavaScript and XML(以及 DHTML 等)的缩写. Ajax 尝试建立桌面应用程序的功能和交互性,与不断更新的 Web 应用程序之间的桥梁.不 ...
- 接口是否可继承(extends)接口?抽象类是否可实现(implements)接口?抽象类是否可继承具体类(concrete class)?
接口可以继承接口,而且支持多重继承.抽象类可以实现(implements)接口,抽象类可继承具体类也可以继承抽象类.
- 解释Spring支持的几种bean的作用域?
Spring框架支持以下五种bean的作用域: singleton :bean在每个Spring ioc 容器中只有一个实例. prototype:一个bean的定义可以有多个实例. request: ...
- AQS分析笔记
1 介绍 AQS: AbstractQueuedSynchronizer,即队列同步器.是构建锁或者其他同步组件的基础框架.它维护了一个volatile int state(代表共享资源)和一个FIF ...
- 什么是消费者驱动的合同(CDC)?
这基本上是用于开发微服务的模式,以便它们可以被外部系统使用.当我们处理 微服务时,有一个特定的提供者构建它,并且有一个或多个使用微服务的消费者. 通常,提供程序在 XML 文档中指定接口.但在消费者驱 ...
- 学习Nginx(三)
nginx的性能测试及常用优化手段 一.nginx的性能测试及对比 1.环境准备 [root@test8_hadoop_kaf ~]# yum install -y httpd-tools [ro ...
