algorithm learning for Leetcode (1)

Leetcode 算法学习（一）

前言：最近学校要求必须学习C++，着重提升技能板块。为了快速升级，我在GitHub上发现了一个开源的学习号召: https://labuladong.github.io/ebook/; 目前我决定跟随lab的步子结合自身规划学习，如果有相同或类似的内容，尊重原创。

这里可以关注lab的公众号，以及lab在github发布的共享，不过在下载他的包之后还是有点懵，排版和安排都很麻烦，幸好有群的存在让我理清了很多盲区。

1. memory of them

我们认为在数据逻辑存储管理中主要由“数组”以及“链表”，两种最基本的存储管理方式。在他们的基础上才派生出“树”、“栈”、“队列”、“图”等上层逻辑。

所以，我们在学习研究他们和他们派生的上层逻辑时，必须先弄清楚他们是怎样在计算机中存储管理的，进而了解为什么它们具有相应的特征，比如数组可以随机访问而链表则不能。

首先，我们的解释器通过read数组的type a和size b分配 b 个a 规格大小的空间(所以超过这个范围就会出错，而且不会报错)。而在数组中我们认为第一个数据块的第一个字节的地址 c 是我们整个数组的地址(我们只将这个地址记录在解释器的表单，换句话说如果你想访问这个数组的任何一个元素则必须通过他的首地址)，在后面的第 n 个数据块的地址就是初始地址 c + n*b。在这个过程中很明显的我们发现我们默认data1结束后下一个地址就是data2，我们没有任何软件层面的跳转的指针，那么他们只能通过物理连续的情况连续排列在一起，所以我们说数组是连续的。

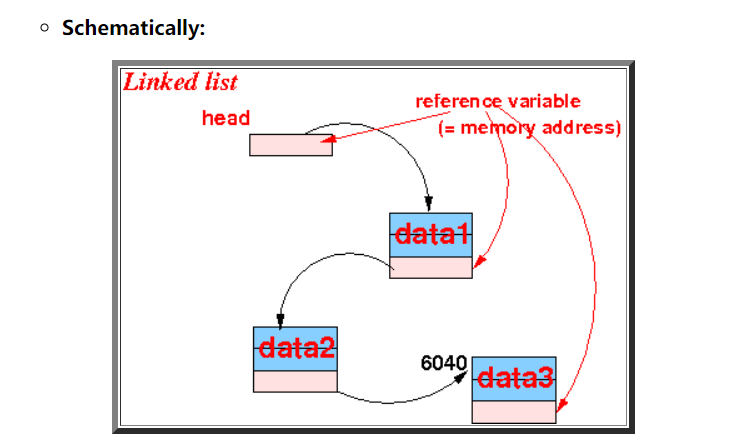
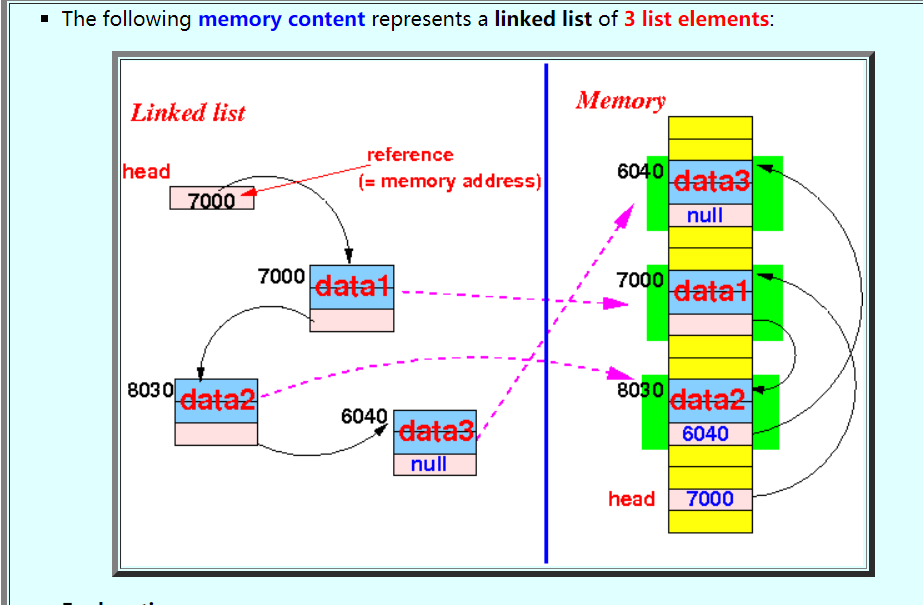
其次，我们再回头说如果我们不要求每个data在物理层面上连续，那么就只能通过软件告诉我们的电脑如何找到下一个data的位置。所以，我们可以通过让每个data[i] 存储data[i+1] 的地址的方式找到这一串的数据。显而易见，这样就意味着我们相对数组就需要更多的空间来存放地址，并且想访问第 n 个数据元素，必须通过第 n-1个元素才能知道，因此我们说链表是顺序的。（注意：和数组一样你仍然只能知道第一个头元素的地址。但是，他和数组不同的是：因为数组在物理地址连续，所以在知道第一个地址的时候，就意味着可以直接通过首地址 c + n*b 的计算方法，直接得到任意元素 n 的地址，但是链表不能直接通过首地址得到任意元素n的地址，必须一个一个的按照顺序访问才能找到。综上所述，我们得出“数组可以随机访问而链表不能随机访问的说法”）

最后，我们说因为数组在分配空间时有一个最大值，当数组空间不够用的时候就会出现错误的读写情况。所以当我们发现数组或者链表空间不够的时候就需要扩容。链表由于没有连续物理空间限制所以不存在这样的问题直接插入即可，时复杂度为O(1), 而数组则需要重新分配一个更大的空间然后把原来的数组复制过去，这样的空间负责度为O（N）。

2. operation

这是lab的原话：数据结构种类很多，但它们存在的目的都是在不同的应用场景，尽可能高效地增删查改。

在这里我们把操作归纳为“线性以及非线性”的“遍历和访问”，并对他们进行梳理和复习。

ok, than, what is the difference between linear and nonlinear in computer?

some commonly used linear data structures are like arrays, linked lists, stacks, and queues.

Data structures like trees and graphs are some examples of nonlinear data structures.

like this.

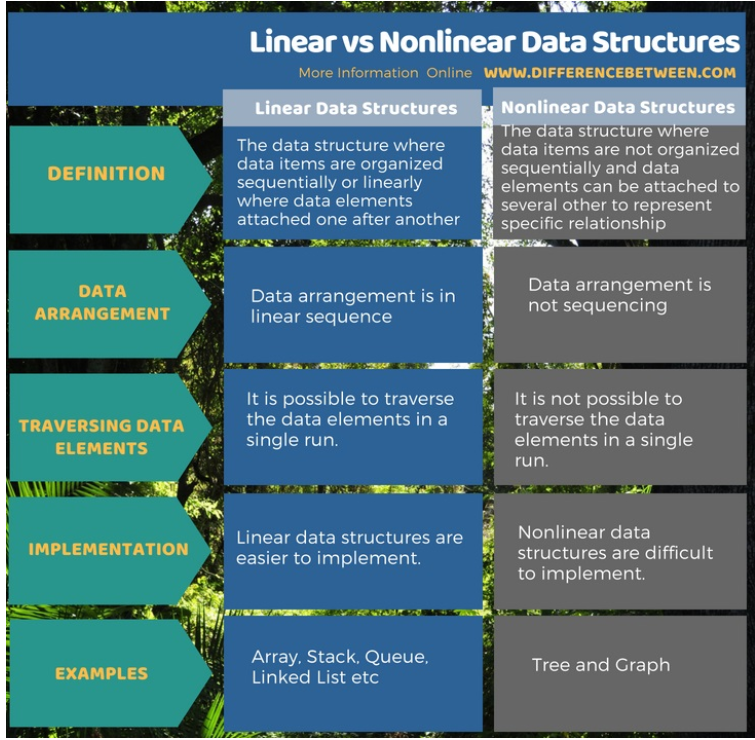
所以综上所述，简单而符合物理存储的是线性的，复杂的、数据组织难以通过顺序方式实现且不能在非线性结构一次性运行完的是非线性的。迭代算法将比递归算法更快，因为要反复调用函数和注册堆栈等开销。很多时候递归算法是无效的，因为它们占用更多的空间和时间。递归算法在应用简单、有效的情况下，多用于求解复杂问题。以Hannoi算法为例，通过递归简化了算法塔的设计，使迭代法得到了广泛的应用，提高了算法的效率。

这是lab的原话：所谓框架，就是套路。不管增删查改，这些代码都是永远无法脱离的结构，你可以把这个结构作为大纲，根据具体问题在框架上添加代码就行。

最后lab推荐从二叉树下手，前 10 道也许有点难受；结合框架再做 20 道，也许你就有点自己的理解了；刷完整个专题，再去做什么回溯动规分治专题，你就会发现只要涉及递归的问题，都是树的问题。