论文解读（ChebyGIN）《Understanding Attention and Generalization in Graph Neural Networks》

论文信息

论文标题：Understanding Attention and Generalization in Graph Neural Networks
论文作者：Boris Knyazev, Graham W. Taylor, Mohamed R. Amer
论文来源：2019,NeurIPS
论文地址：download
论文代码：download

1 Introduction

　　本文关注将注意力 GNNs 推广到更大、更复杂或有噪声的图。作者发现在某些情况下，注意力机制的影响可以忽略不计，甚至有害，但在某些条件下，它给一些分类任务带来了超过 60% 的额外收益。

2 Attention meets pooling in graph neural networks

　　注意力机制可以用在边上，也可以用在节点上，传统的 GAT 是用在边上，本文更关注于节点上的注意力机制。

　　注意力机制在CNN里一般用以下公式表达：

　　　　$Z=\alpha \odot X  \quad\quad\quad(1)$

　　其中:

• • $X \in \mathbb{R}^{N \times C}$ 代表输入；
  • $Z_{i}=\alpha_{i} X_{i}$ 是使用注意力机制后的输出；
  • $\alpha$ 是注意力系数，并有 $\sum_{i}^{N} \alpha_{i}=1$；

　　在 Graph U-Nets​ 的 $\text{Eq.2}$ 中，同样使用到了注意力机制：

　　　　$Z_{i}=\left\{\begin{array}{ll}\alpha_{i} X_{i}, & \forall i \in P \\\emptyset, & \text { otherwise }\end{array}\right.\quad\quad\quad(2)$

　　其中：

• • $P$ 是一组集合节点的索引，且有 $|P| \leq N$；
  • $\emptyset$ 表示输出中不存在该单元；

　　本文的 $\text{Eq.2}$ 和 $\text{Eq.1}$ 的不同之处在于，在 Graph U-Nets 中 $Z \in \mathbb{R}^{|P| \times C}$ 表明只使用了部分节点，即保存了 $r=|P| / N \leq 1$ 部分的节点。

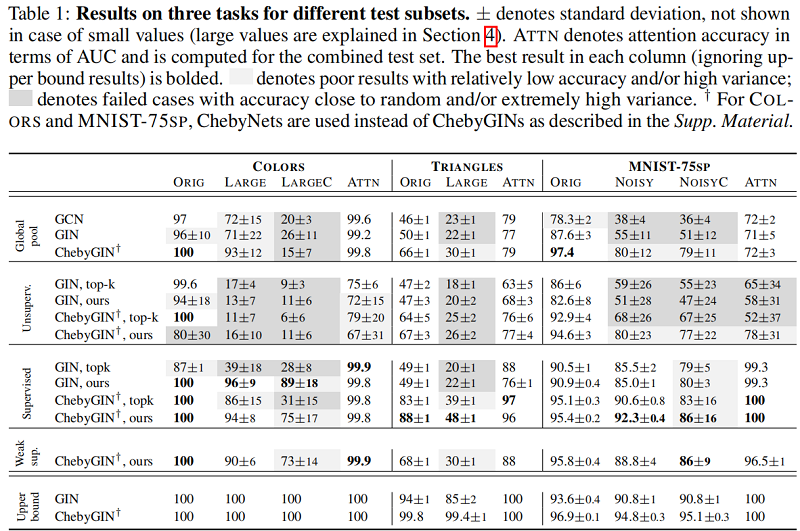
　　本文设计了两个简单的图形推理任务，让我们在一个受控环境中研究注意力，了解地面真实注意力。第一个任务是计算图中的颜色，其中颜色是一个唯一的离散特征。第二个任务是计算图形中的三角形的数量。​我们在一个标准基准，MNIST[13]（Figure1）上证实了我们的观察结果，并确定了影响注意力有效性的因素。​

　　

3 Model

　　本文研究了两种GNNs：GCN 和 GIN，其中 GIN 将原有的 MEAN aggregator 替换为 SUM aggregator，然后使用一个 FC 层。

3.1 Thresholding by attention coefficients

　　使用 Graph U-Nets 中的方法，需要使用预定义的比率 $r=|P| / N$  为整个数据集选择节点。比如对每个 pooling 设置 r = 0.8 即 80% 的节点被保存下来。直观地说，对于大小不同的图，这个比率应该是不同的。因此，建议选择阈值 $\tilde{\alpha}$，这样就只传播具有注意值 $\alpha_{i}>\tilde{\alpha}$ 的节点：

　　　　$Z_{i}=\left\{\begin{array}{ll}\alpha_{i} X_{i}, & \forall i: \alpha_{i}>\tilde{\alpha} \\\emptyset, & \text { otherwise }\end{array}\right. \quad\quad\quad(3)$

　　Note：图中删除的节点不同于保存的节点，其特征的值是非常小的，甚至为 $0$。在本实验中，相近邻域的节点通常有相似 $\alpha$ ，因此整个局部邻域被合并或者丢弃，而不是基于聚类的方法将每个邻域压缩为单个节点。

3.2 Attention subnetwork

　　为了训练一个预测节点系数的注意模型，我们考虑了两种方法：

• • Linear Projection[11]：只有单层投影 $\mathbf{p} \in \mathbb{R}^{C}$ 需要被训练：$\alpha_{\text {pre }}=X \mathbf{p}​$；
  • DiffPool[10]，其中训练了一个单独的 GNN：$\alpha_{\text {pre }}=X \mathbf{p}​$；

　　在所有情况下，我们在[11]中使用 softmax 激活函数而不是 tanh，因为它提供了更可解释的结果和稀疏输出：$\alpha=\operatorname{softmax}\left(\alpha_{p r e}\right)$ 。为了以监督或弱监督的方式训练注意力，我们使用 KL 散度损失。

3.3 ChebyGIN

　　有些结果下，GCNs 和 GINs 表现的较差，本文将 GIN 和 ChebyNet 进行融合，研究了 $K=2$ 的 ChebyGIN。

4 Experiments

4.1 Datasets

COLORS

　　本文引入了颜色计数任务，即统计图中绿色的节点有多少个，对于绿色节点设置 注意力系数为 $\alpha_{i}^{G T}=1 / N_{\text {green }}$。

TRIANGLES

　　统计图中有多少个三角形？显然一个简单 的方法是计算：$\operatorname{trace}\left(A^{3}\right) / 6$ 。

　　接着对每个节点设置注意力系数：$\alpha_{i}^{G T}=T_{i} / \sum\limits _{i} T_{i}$，其中 $T_{i}$ 是多少个三角形包含节点 $i$。

MNIST-75SP

 

　　该任务的目的是识别出图片代表的数字是多少，其中图片为 $0-9$ 的数字。具体方法是先用 SLIC 算法生成超像素快，然后构建图。每个节点对应一个超像素块。然后 $\alpha$ 系数的初始值的计算公式为：$\alpha_{i}^{G T}=1 / N_{\text {nonzero }}$ ，$N_{\text {nonzero }}$ 是这些超像素的总数。

4.2 Generalization to larger and noisy graphs

　　为了验证注意力机制的健壮性，作者将颜色实验和三角形实验引入到更大的网络之中。如图：

　　

　　在颜色实验中添加了另外一个通道，变成 $4$ 个通道 [ c_1,c_2,c_3,c_3 ]，然后其中 [0,1,0,0] 的时候代表绿色，其他的时候 $[c_1,0,c_3,c_4]$ 其中 $c_1$，$c_3$，$c_4$，可以是 $0-1$ 之间的数值，代表红色，蓝色，透明色的三种颜色的混合。

　　在三角形计数实验中，也引入了更多的节点数。

　　在MNIST数据集的实验中，加入了高斯噪音，是的模型的识别度更高。

4.3 Network architectures and training

　　对于 COLORS 和 TRIANGLES，我们最小化了其他任务的回归损失(MSE)和交叉熵(CE)，对于有监督和弱监督实验，本文还最小化了 ground truth attention $\alpha^{G T}$ 和 predicted coefficients $\alpha$ 之间的 KL 散度。

　　　　$\mathcal{L}=\mathcal{L}_{M S E / C E}+\frac{\beta}{N} \sum\limits _{i} \alpha_{i}^{G T} \log \left(\frac{\alpha_{i}^{G T}}{\alpha_{i}}\right)   \quad\quad\quad(5)$

　　为了评估注意力系数的正确性，遵循CNN的方式，我们在训练完一个模型之后呢，移除这个节点，再计算预测一个标签，计算与原始标签的差异，这样来计算出一个评估的 $\alpha$ 系数：

　　　　$\alpha_{i}^{W S}=\frac{\left|y_{i}-y\right|}{\sum\limits _{j=1}^{N}\left|y_{j}-y\right|}$

5 Experiments

　　

6 Conclusion

　　证明了注意力对于图神经网络是非常强大的，但是由于初始注意力系数的敏感性，要达到最优是很困难的。特别是在无监督的环境中，由于不能确定初始注意力系数的值，使得这样的训练更加困难。我们还表明，注意力可以使GNN对更大，更嘈杂的图形有更强的能力。同时本文提出的弱监督模型和有监督模型具有相似的优势性。