python 动态规划（背包问题和最长公共子串）

背包问题

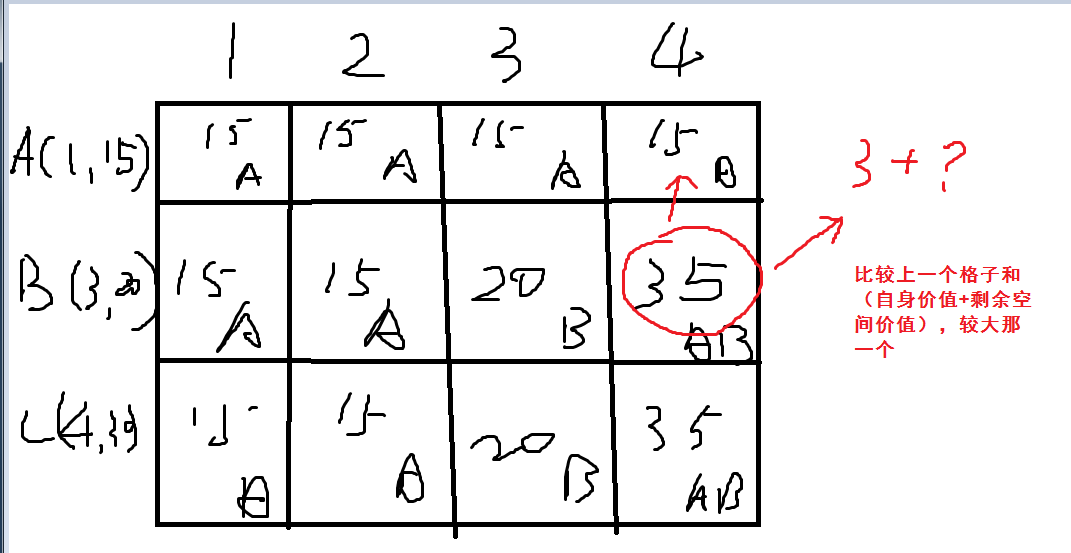
现在要往一个可以装4个单位重量的背包里怎么装价值最高：A重量1个单位，价值15；B重量3个单位，价值20；C重量4个重量，价值30

使用动态规划填充空格

class SolutionBag:
    def valuableBag(self,optionalList,sizeBig):
        #创建网格
        grid = [[0 for i in range(sizeBig+1)] for j in range(len(optionalList)+1)]
        #从行列序号1开始计数
        column = 1
        for v in optionalList.values():
            optionalWeight,optionalPrice = v
            for row in range(sizeBig):
                if optionalWeight > row+1:
                    grid[column][row+1] = grid[column-1][row+1]
                else:
                    grid[column][row+1] = max(grid[column-1][row+1],optionalPrice+grid[column-1][row+1-optionalWeight])
            column += 1

        return grid

#SolutionBag().valuableBag({"A":(1,15),"B":(3,20),"C":(4,30)},4)

最长公共子串

在动态规划中，你要将某个指标最大化。在这个例子中，你要找出两个单词的最长公共子串。fish和fosh都包含的最长子串是什么呢

如何将这个问题划分为子问题呢？你可能需要比较子串：不是比较hish和fish，而是先比较his和fis

我们网格填充的方法来实现

#伪代码

#字母相同则左上方+1
if word1[i] == word2[j] :
    cell[i][j] = cell[i-1][j-1] +1
else:
    cell[i][j] = max(cell[i][j-1],cell[i-1][j])

python实现网格

class SolutionLengthS:
    def longestLength(self,str1,str2):
        grid = [[0 for j in range(len(str2)+1)] for i in range(len(str1)+1)]
        for i in range(len(str2)):
            for j in range(len(str1)):
                if str1[j] == str2[i] :
                    grid[i+1][j+1] = grid[i][j] + 1
                else:
                    grid[i+1][j+1] = max(grid[i+1][j],grid[i][j+1])
        return grid