Java数据结构和算法（一）概念

数据结构和算法（一）复杂度分析

数据结构与算法目录(https://www.cnblogs.com/binarylei/p/10115867.html)

目录

• 数据结构和算法（一）复杂度分析
  • 1. 时间复杂度
    • 1.1 什么是时间复杂度
    • 1.2 时间复杂度分析
    • 1.3 常见的时间复杂度
    • 1.4 主定律
    • 1.5 最好、最坏、平均、均摊时间复杂度
  • 2.2 空间复杂度

数据结构和算法本身解决的是 "快" 和 "省" 的问题，即如何让代码运行得更快，如何让代码更省存储空间。所以，执行效率是算法一个非常重要的考量指标。那如何来衡量你编写的算法代码的执行效率呢？这里就要用：时间复杂度和空间复杂度分析。

复杂度分析是整个算法学习的精髓，只要掌握了它，数据结构和算法的内容基本上就掌握了一半。

1. 时间复杂度

1.1 什么是时间复杂度

一个算法花费的时间与算法中语句的执行次数成正比例，哪个算法中语句执行次数多，它花费时间就多。一个算法中的语句执行次数称为语句频度或时间频度。记为 T(n)。

在刚才提到的时间频度中，n 称为问题的规模，当 n 不断变化时，时间频度 T(n) 也会不断变化。但有时我们想知道它变化时呈现什么规律。为此，我们引入时间复杂度概念。

一般情况下，算法中基本操作重复执行的次数是问题规模 n 的某个函数，用 T(n) 表示，若有某个辅助函数 f(n)，使得当 n 趋近于无穷大时，T(n) / f(n) 的极限值为不等于零的常数，则称 f(n) 是 T(n) 的同数量级函数。记作 T(n) = O(f(n))，称 O(f(n)) 为算法的渐进时间复杂度，简称时间复杂度。

• 随着问题规模 n 的增大，常数部分的影响越来越小
  
  T(n) = 2n² + 4n +log₂n + 4

• 随着问题规模 n 的増大，增长最快的项影响越来越大
  
  T(n) = 2n² + 4n + log₂n + 4

• 渐进时间复杂度只关注增长最快的项
  
  T(n) = O(n²) // 去除常数系数，去除复杂度小的项

• logn 一般表示 log₂n

有时候，算法中基本操作重复执行的次数还随问题的输入数据集不同而不同，如在冒泡排序中，输入数据有序而无序，其结果是不一样的。此时，我们计算平均值。

1.2 时间复杂度分析

（1）只关注循环执行次数最多的一段代码

（2）加法法则：总复杂度等于量级最大的那段代码的复杂度

（3）乘法法则：嵌套代码的复杂度等于嵌套内外代码复杂度的乘积

实例 1： T(n) = 1 + n + 2n² = O(n²)

sum = 0;                   // 执行 1 次
for(i = 1; i <= n; i++)    // 执行 n 次
    for(j = 1;j <= n;j++)  // 执行 n^2 次
        sum++;             // 执行 n^2 次

实例 2：T(n) = 1 + 4n = O(n)

a = 0;  b= 1;                // 执行 1 次
for (i = 1; i <= n; i++) {   // 执行 n 次
    s = a + b;               // 执行 n 次
    b = a;                   // 执行 n 次
    a = s;                   // 执行 n 次
}

实例 3：T(n) = O(log₂n)

i = 1;            // 执行 1 次
while (i <= n)
    i = i * 2;    // 设频度是 f(n)，则：2^f(n)<=n; f(n)<=log2n

1.3 常见的时间复杂度

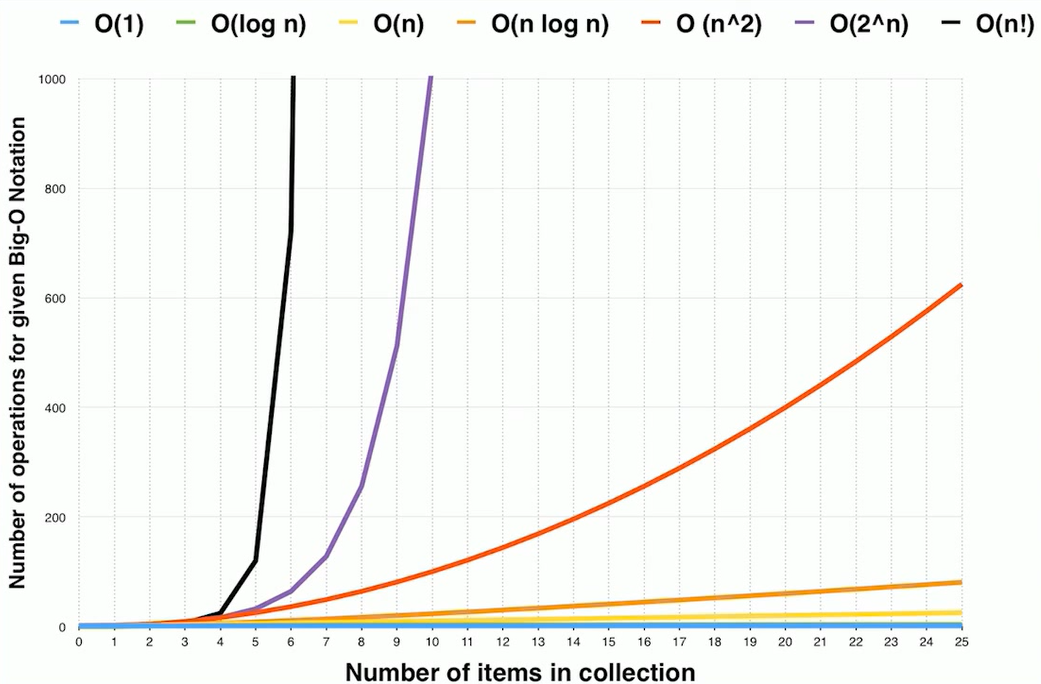
虽然代码千差万别，但是常见的复杂度量级并不多。我稍微总结了一下，这些复杂度量级几乎涵盖了你今后可以接触的所有代码的复杂度量级。对于以下复杂度量级，可以粗略地分为两类，多项式量级和非多项式量级。其中，非多项式量级只有两个：O(2n) 和 O(n!)，执行效率也非常低。

1. 常量阶 O(1)
2. 对数阶 O(logn)
3. 线性阶 O(n)
4. 线性对数阶 O(nlogn)
5. 平方阶 O(n²) O(n³) O(n⁴)
6. 指数阶 O(2ⁿ)：不常见
7. 阶乘阶 O(n!)：不常见

常见的算法的时间复杂度之间的关系为：

O(1) < O(logn) < O(n) < O(nlogn) < O(n²) < O(2ⁿ)<O(n!) < O(nⁿ)

1.4 主定律

1.5 最好、最坏、平均、均摊时间复杂度

1. 最好情况时间复杂度：代码在最坏情况下执行的时间复杂度。（少使用）
2. 最坏情况时间复杂度：代码在最理想情况下执行的时间复杂度。（少使用）
3. 平均时间复杂度：用代码在所有情况下执行的次数的加权平均值表示。（少使用）
4. 均摊时间复杂度：在代码执行的所有复杂度情况中绝大部分是低级别的复杂度，个别情况是高级别复杂度且发生具有时序关系时，可以将个别高级别复杂度均摊到低级别复杂度上，也叫摊还算法。（极少使用）

下面以一段代码示例，对上述 4 个概念进行简单的分析。

int arr[] = new int[10];
int len = 10;
int i = 0;

void add(int element) {    // 插入元素时，如果空间不够，先扩容再插入
    if (i >= len) {
        int newArr[] = new int[len * 2];
        for (int j = 0; j < len; ++j) {
            newArr[j] = arr[j];
        }
        arr = newArr;
        len = 2 * len;
    }
    arr[i] = element;
    ++i;
}

上述示例：最好是 O(1)，最坏是O(n)，平均和均摊都是O(1)。

摊还算法分析，执行 n 次 O(1) 插入后会执行一次 O(n) 插入，那么我们可以将这次 O(n) 插入公摊到 n 次操作上，这样均摊后仍是 O(1)。

个人体会：平均和平摊基本就是一个概念，平摊是特殊的平均。在分析时间复杂度是 O(1) 还是 O(n) 的时候最简单就是凭感觉，出现 O(1) 的次数远大于出现 O(n) 出现的次数，那么平均平摊时间复杂度就是O(1)。

2.2 空间复杂度

空间复杂度：算法所需存储空间的度量，记作： S(n) = O(f(n))，其中 n 为问题的规模。

我们常见的空间复杂度就是 O(1)、O(n)、O(n²)，像 O(logn)、O(nlogn) 这样的对数阶复杂度平时都用不到。如下代码空间复杂度 O(n)。

int i = 0;                     // 申请空间大小为 1
int[] arr = new int[n];        // 申请空间大小为 n 的数组
for (i; i < n; i++) {
    arr[i] = i;
}

一个算法在计算机存储器上所占用的存储空间，包括存储算法本身所占用的存储空间，算法的输入输出数据所占用的存储空间和算法在运行过程中临时占用的存储空间这三个方面。如果额外空间相对于输入数据量来说是个常数，则称此算法是原地工作。

算法的输入输出数据所占用的存储空间是由要解决的问题决定的，是通过参数表由调用函数传递而来的，它不随本算法的不同而改变。存储算法本身所占用的存储空间与算法书写的长短成正比，要压缩这方面的存储空间，就必须编写出较短的算法。

---

每天用心记录一点点。内容也许不重要，但习惯很重要！