维诺图（Voronoi Diagram）分析与实现（转）

一、问题描述
1.Voronoi图的定义
又叫泰森多边形或Dirichlet图，它是由一组由连接两邻点直线的垂直平分线组成的连续多边形组成。

2.Voronoi图的特点
（1）每个V多边形内有一个生成元；
（2）每个V多边形内点到该生成元距离短于到其它生成元距离；
（3）多边形边界上的点到生成此边界的生成元距离相等；
（4）邻接图形的Voronoi多边形界线以原邻接界线作为子集。

3.Voronoi的应用
在计算几何学科中的重要地位，由于其根据点集划分的区域到点的距离最近的特点，其在地理学、气象学、结晶学、航天、核物理学、机器人等领域具有广泛的应用。如在障碍物点集中，规避障碍寻找最佳路径。

二、算法分析与设计
Voronoi图有着按距离划分邻近区域的普遍特性，应用范围广。生成V图的方法很多，常见的有分治法、扫描线算法和Delaunay三角剖分算法。

1.建立Voronoi图方法和步骤
本次实验采用的是Delaunay三角剖分算法。主要是指生成Voronoi图时先生成其对偶元Delaunay三角网，再找出三角网每一三角形的外接圆圆心，最后连接相邻三角形的外接圆圆心，形成以每一三角形顶点为生成元的多边形网。如下图所示。

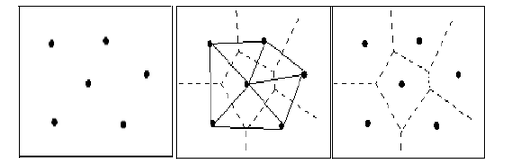
建立Voronoi图算法的关键是对离散数据点合理地连成三角网，即构建Delaunay三角网。
建立Voronoi图的步骤为：
（1）离散点自动构建三角网，即构建Delaunay三角网。对离散点和形成的三角形编号，记录每个三角形是由哪三个离散点构成的。
（2）计算每个三角形的外接圆圆心，并记录之。
（3）遍历三角形链表，寻找与当前三角形pTri三边共边的相邻三角形TriA，TriB和TriC。
（4）如果找到，则把寻找到的三角形的外心与pTri的外心连接，存入维诺边链表中。如果找不到，则求出最外边的中垂线射线存入维诺边链表中。
（5）遍历结束，所有维诺边被找到，根据边画出维诺图。

2. Delaunay三角网的生成
建立Voronoi图的关键是Delaunay三角网的生成。Delaunay三角网的特性：
（1）空圆性，任一三角形外接圆内部不包含其他点。
（2）最接近：以最近临的三点形成三角形，且各线段(三角形的边)皆不相交。
（3）唯一性：不论从区域何处开始构建，最终都将得到一致的结果。
（4）最优性：任意两个相邻三角形形成的凸四边形的对角线如果可以互换的话，那么两个三角形六个内角中最小的角度不会变大。
（5）最规则：如果将三角网中的每个三角形的最小角进行升序排列，则Delaunay三角网的排列得到的数值最大。
（6）区域性：新增、删除、移动某一个顶点时只会影响临近的三角形。
（7）具有凸多边形的外壳：三角网最外层的边界形成一个凸多边形的外壳。
Delaunay剖分是一种三角剖分的标准，实现它有多种算法。本次采用Bowyer-Watson算法，算法的基本步骤是：
（1）构造一个超级三角形，包含所有散点，放入三角形链表。
（2）将点集中的散点依次插入，在三角形链表中找出其外接圆包含
插入点的三角形（称为该点的影响三角形），删除影响三角形的公共边，将插入点同影响三角形的全部顶点连接起来，从而完成一个点在Delaunay三角形链表中的插入。
（3）根据优化准则对局部新形成的三角形进行优化。将形成的三角形放入Delaunay三角形链表。
（4）循环执行上述第2步，直到所有散点插入完毕。

关键步骤2如下图所示：

步骤3的局部优化的准则指的是：
1.对新形成的三角形进行优化，将两个具有共同边的三角形合成一个多边形。
2.以最大空圆准则作检查，看其第四个顶点是否在三角形的外接圆之内。
3.如果在，修正对角线即将对角线对调，即完成局部优化过程的处理。

LOP (Local Optimization Procedure)处理过程如下图所示：

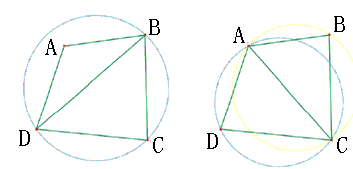
3.数据结构的设计
本程序的实现采用C#面向对象语言实现，故数据结构的设计采用类的形式，具体有：

点：
    public class Site
    {
        public double x, y;
        public Site()
        { }
        public Site(double x, double y)
        {
            this.x = x;
            this.y = y;
        }
    }
边：
    public class Edge
    {
        public Site a, b;
        public Edge(Site a, Site b)
        {
            this.a = a;
            this.b = b;
        }
    }
三角形：
    public class DelaunayTriangle
    {
        Voronoi voronoi = new Voronoi();
        public Site site1, site2, site3;//三角形三点
        public Site centerPoint;//外界圆圆心
        public double radius;//外接圆半径
        public List<DelaunayTriangle> adjoinTriangle;//邻接三角形 

        public DelaunayTriangle(Site site1,Site site2,Site site3)
        {
            centerPoint = new Site();
            this.site1 = site1;
            this.site2 = site2;
            this.site3 = site3;
            //构造外接圆圆心以及半径
            voronoi.circle_center(centerPoint, site1, site2,site3,ref radius);
        }
    }

4. 算法复杂度分析
时间复杂度：
Delaunay三角网的生成的时间复杂度：
步骤一：构造一个超级三角形，O（1）；
步骤二：产找影响的三角形，构造新的三角形，O（1+2+…+n）=O(n2)O（1+2+…+n）=O(n2)
步骤三：对新形成的三角形进行优化局部优化：O(n)。
因此，整体时间复杂度是：O(1)+O(n2)+O(n)=O(n2)O(1)+O(n2)+O(n)=O(n2)。

从Delaunay三角网生成Voronoi图的时间复杂度：
步骤一：构造构建Delaunay三角网，O(n2)O(n2)；
步骤二：计算三角形外接圆圆心，O(n)；
步骤三：寻找三角形三边相邻三角形：3O(n)；
步骤四：找到的维诺边存入链表中，画出维诺图：O(n)。
因此，整体时间复杂度是O(n2)+O(n)+3O(n)+O(n)=O(n2)O(n2)+O(n)+3O(n)+O(n)=O(n2)。

三、实验结果
随机生成点：

生成Delaunay三角形网：

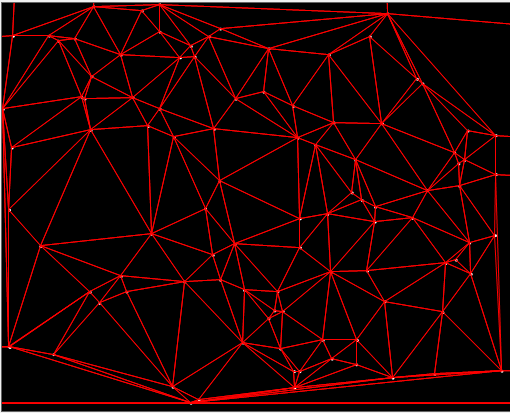
生成Voronoi图：

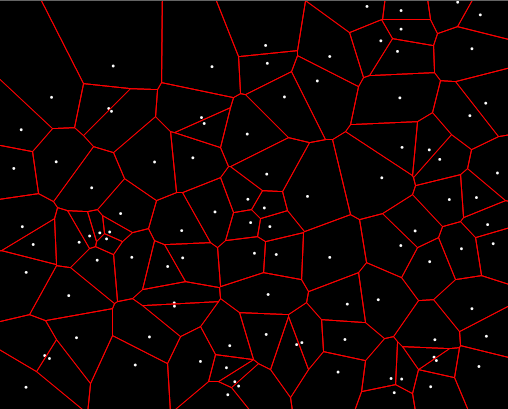
生成Voronoi图的可执行程序和源码工程文件见here。

下面附上相关函数申明（详细代码见源码工程文件）。

//根据点集构造Delaunay三角形网
public void setDelaunayTriangle(List<DelaunayTriangle> allTriangle, List<Site> sites);

//根据Delaunay三角形网构造Voronoi图的边
public List<Edge> returnVoronoiEdgesFromDelaunayTriangles(List<DelaunayTriangle> allTriangle, List<Edge> voronoiRayEdgeList);

//根据三角形链表返回三角形所有的边
public List<Edge> returnEdgesofTriangleList(List<DelaunayTriangle> allTriangle);

//对新形成的三角形进行局部优化
public List<DelaunayTriangle> LOP(List<DelaunayTriangle> newTriList);

//判断边是否属于三角形
public bool isEdgeOnTriangle(DelaunayTriangle triangel,Edge edge);

//判断点是否属于三角形
public bool isPointOnTriangle(DelaunayTriangle triangle, Site site);

//将点与受影响的三角形三点连接，形成新的三个三角形添加到三角形链中
public void addNewDelaunayTriangle(List<DelaunayTriangle> allTriangles,DelaunayTriangle influenedTri,Site point);

//找出受影响的三角形的公共边
public List<Edge> findCommonEdges(List<DelaunayTriangle> influenedTriangles);

//找出两个三角形的公共边
public Edge findCommonEdge(DelaunayTriangle chgTri1, DelaunayTriangle chgTri2);

//判断插入点是否在三角形边上
public Site[] isOnEdges(DelaunayTriangle triangle,Site site);  

//判断点是否在三角形外接圆的内部
public bool isInCircle(DelaunayTriangle triangle, Site site) ;

//求三角形的外接圆心
public void circle_center(Site center, Site sites0, Site sites1, Site sites2, ref double radius) ;

//求两点之间距离
public double distance2Point(Site p,Site p2);

原文：https://blog.csdn.net/k346k346/article/details/52244123