hdu3714 三分

Error Curves

Time Limit: 4000/2000 MS (Java/Others)    Memory Limit: 65536/65536 K (Java/Others)
Total Submission(s): 4590    Accepted Submission(s): 1753

Problem Description

Josephina is a clever girl and addicted to Machine Learning recently. She
pays much attention to a method called Linear Discriminant Analysis, which
has many interesting properties.
In order to test the algorithm's efficiency, she collects many datasets.
What's more, each data is divided into two parts: training data and test
data. She gets the parameters of the model on training data and test the
model on test data. To her surprise, she finds each dataset's test error curve is just a parabolic curve. A parabolic curve corresponds to a quadratic function. In mathematics, a quadratic function is a polynomial function of the form f(x) = ax2 + bx + c. The quadratic will degrade to linear function if a = 0.

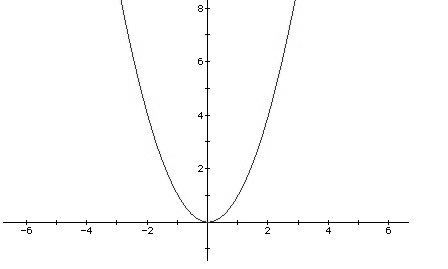
It's very easy to calculate the minimal error if there is only one test error curve. However, there are several datasets, which means Josephina will obtain many parabolic curves. Josephina wants to get the tuned parameters that make the best performance on all datasets. So she should take all error curves into account, i.e., she has to deal with many quadric functions and make a new error definition to represent the total error. Now, she focuses on the following new function's minimum which related to multiple quadric functions. The new function F(x) is defined as follows: F(x) = max(Si(x)), i = 1...n. The domain of x is [0, 1000]. Si(x) is a quadric function. Josephina wonders the minimum of F(x). Unfortunately, it's too hard for her to solve this problem. As a super programmer, can you help her?

 

Input

The input contains multiple test cases. The first line is the number of cases T (T < 100). Each case begins with a number n (n ≤ 10000). Following n lines, each line contains three integers a (0 ≤ a ≤ 100), b (|b| ≤ 5000), c (|c| ≤ 5000), which mean the corresponding coefficients of a quadratic function.

 

Output

For each test case, output the answer in a line. Round to 4 digits after the decimal point.

 

Sample Input

2
1
2 0 0
2
2 0 0
2 -4 2

 

Sample Output

0.0000
0.5000

题目大意：mdzz，英语不好的我理解了半天才搞懂，就是给你若干个二维函数，让你在[0,1000]这个区间里

确定由这些函数最大值连接起来新函数图像的最小值。

思路分析：

光说不练假把式orz，画一下图就可以发现这是一个单峰函数，很明显可以用三分来做，注意精度，听说开到

1e-9才不会wa，试了一下，果然1A了，我发现，当三分问题和几何问题结合的时候一定要记得画图，这样可

以更容易看出这道题的特点。

代码：

#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <queue>
#include <stack>
using namespace std;
const int maxn=10000+100;
const double eps=1e-9;
const int inf=0xfffffff;
int n;
struct nod
{
    double a;
    double b;
    double c;
};
nod f[maxn];
double cal(double x)
{
    double maxn=-inf;
    for(int i=0;i<n;i++)
    {
       maxn=max(maxn,f[i].a*x*x+f[i].b*x+f[i].c);
    }
    return maxn;
}
int main()
{
    int T;
    scanf("%d",&T);
    while(T--)
    {
        scanf("%d",&n);
        for(int i=0;i<n;i++)
          scanf("%lf%lf%lf",&f[i].a,&f[i].b,&f[i].c);
        double l=0,r=1000;
        while(l+eps<=r)
        {
            double mid=(l+r)/2;
            double mmid=(mid+r)/2;
            if(cal(mid)<=cal(mmid))  r=mmid;
            else l=mid;
        }
        printf("%.4lf\n",cal(l));
    }
    return 0;
}