LibreOJ 6004 圆桌聚餐 (最大流)

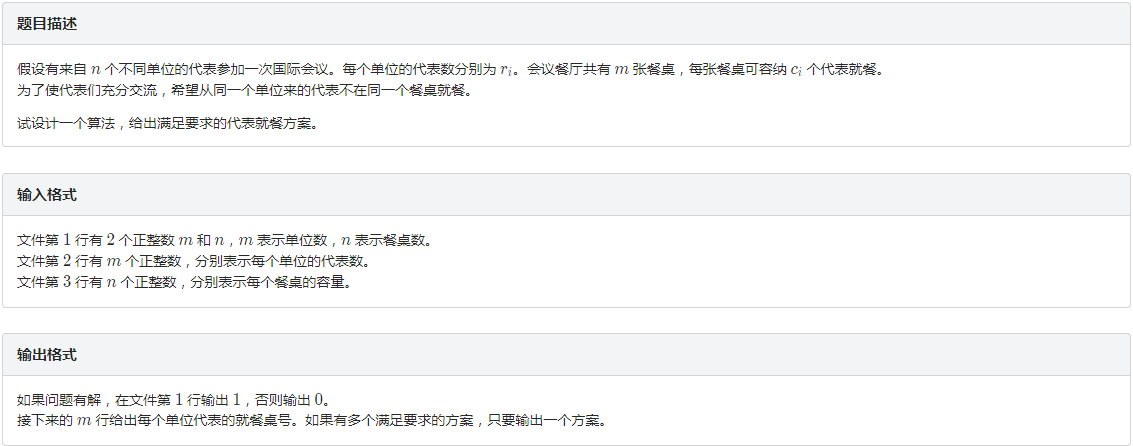
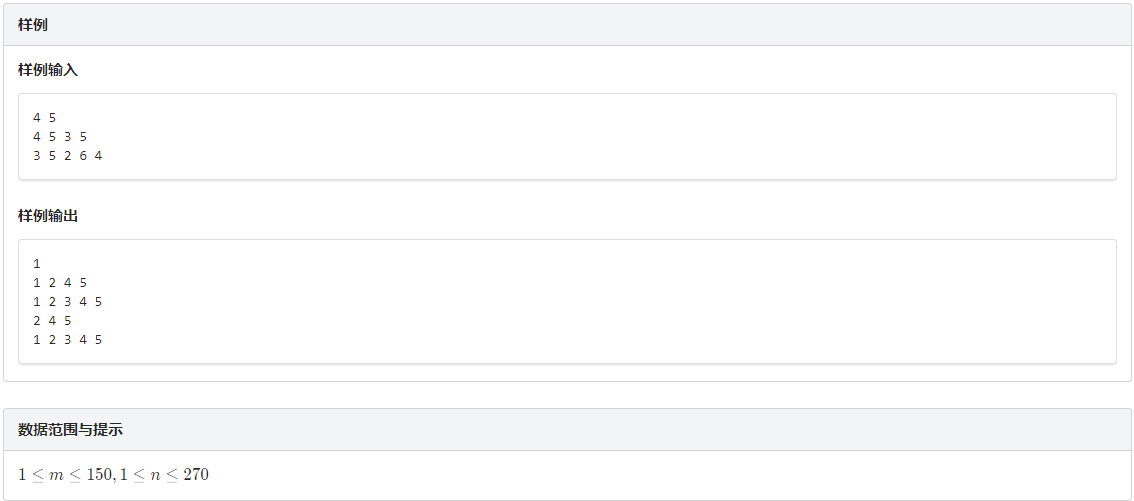
题解:天啊,这道最大流真是水的一批……只需要每张桌子向每个单位建一条容量为1的边,源点向桌子建边,容量为桌子能坐的人数;单位向汇点建边,容量为单位人数即可,然后根据单位与桌子的连边值是否为一来了解每个单位配对的桌子即可

代码如下:

#include<queue>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define inf 0x3f3f3f3f
using namespace std;

int head[],next[],w[],v[],deep[],cur[];
int n,m,s,t,cnt;

int init()
{
    cnt=-;
    memset(head,-,sizeof(head));
    memset(next,-,sizeof(next));
}

void add(int from,int to,int cost)
{
    cnt++;
    next[cnt]=head[from];
    w[cnt]=cost;
    v[cnt]=to;
    head[from]=cnt;
} 

void add_edge(int from,int to,int cost)
{
    add(from,to,cost);
    add(to,from,);
}

int bfs(int s,int t)
{
    queue<int> q;
    memset(deep,,sizeof(deep));
    deep[s]=;
    q.push(s);
    while(!q.empty())
    {
        int u=q.front();
        q.pop();
        for(int i=head[u];i!=-;i=next[i])
        {
            if(w[i]>&&!(deep[v[i]]))
            {
                deep[v[i]]=deep[u]+;
                q.push(v[i]);
            }
        }
    }
    if(!deep[t])
    {
        return ;
    }
    return ;
}

int dfs(int u,int t,int dist)
{
    if(u==t)
    {
        return dist;
    }
    for(int &i=cur[u];i!=-;i=next[i])
    {
        if(deep[v[i]]==deep[u]+&&w[i]!=)
        {
            int di=dfs(v[i],t,min(dist,w[i]));
            if(di>)
            {
                w[i]-=di;
                w[i^]+=di;
                return di;
            }
        }
    }
    return ;
}

int dinic(int s,int t)
{
    int res=;
    while(bfs(s,t))
    {
        for(int i=s;i<=t;i++)
        {
            cur[i]=head[i];
        }
        while(int di=dfs(s,t,inf))
        {
            res+=di;
        }
    }
    return res;
}

int main()
{
    int a[],b[],sum=;
    vector<int> g[];
    scanf("%d%d",&m,&n);
    init();
    s=;t=n+m+;
    for(int i=;i<=m;i++)
    {
        scanf("%d",&a[i]);
        add_edge(i+n,t,a[i]);
        sum+=a[i];

    }
    for(int i=;i<=n;i++)
    {
        scanf("%d",&b[i]);
        add_edge(s,i,b[i]);
        for(int j=;j<=m;j++)
        {
            add_edge(i,j+n,);
        }
    }
    int ans=dinic(s,t);
    if(ans==sum)
    {
        puts("");
    }
    else
    {
        puts("");
        return ;
    }
    for(int i=head[t];i!=-;i=next[i])
    {
        for(int j=head[v[i]];j!=-;j=next[j])
        {
            if(w[j]&&v[j]!=t)
            {
                g[v[i]-n].push_back(v[j]);
            }
        }
    }
    for(int i=;i<=n;i++)
    {
        for(int j=;j<g[i].size();j++)
        {
            printf("%d ",g[i][j]);
        }
        printf("\n");
    }
}