a) setter(重要)

 <property name="userDAO">

       <ref bean="u"/>

 </property>

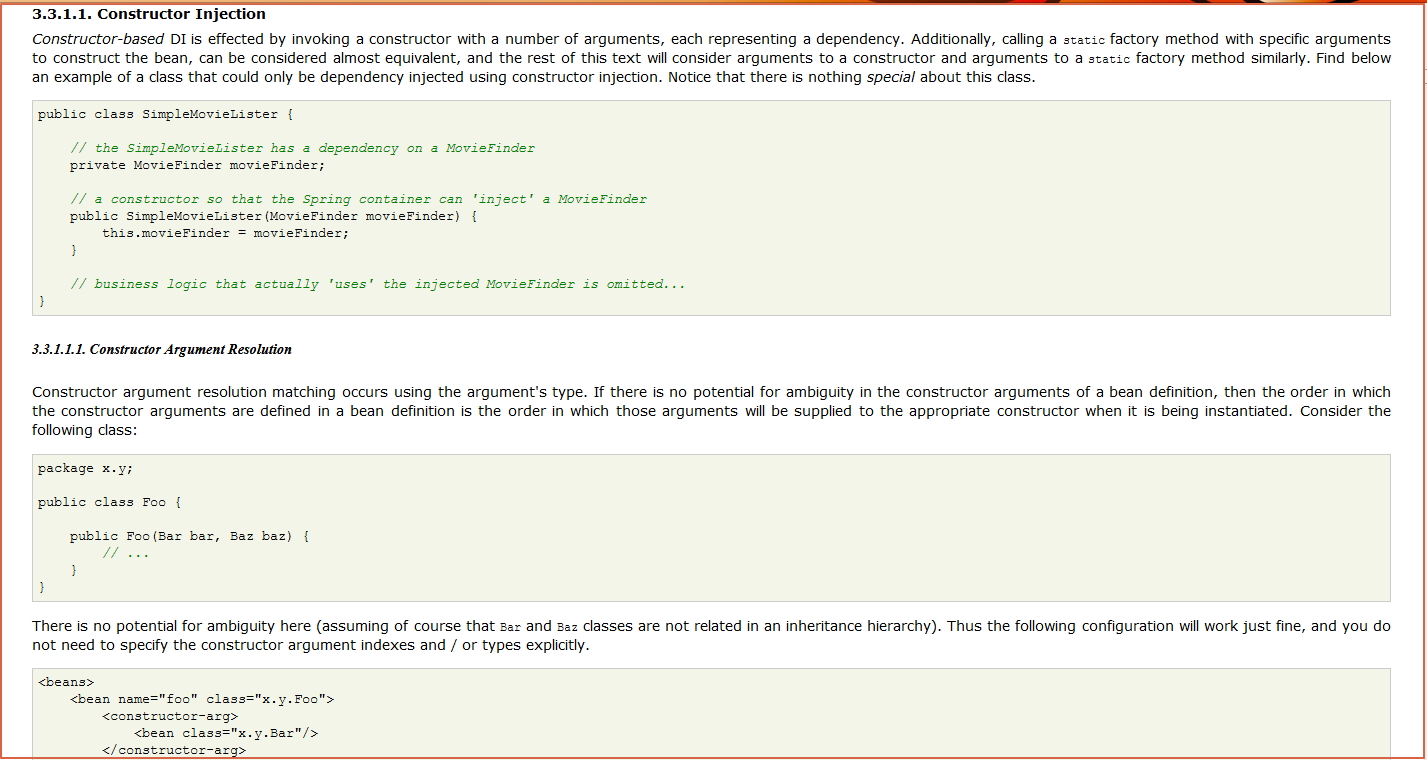
b) 构造方法(可以忘记)，简单例子：

 <constructor-arg>

     <ref bean="u"/>

 </constructor-arg>

用的不多，具体的构造函数重构应用可以参考源文档

c) 接口注入(可以忘记)。

代码链接: http://pan.baidu.com/s/1pKAe5Vt 密码: qvyy

jar 包:

　　链接: http://pan.baidu.com/s/1i4M2dfv 密码: hdbd

注入类型(Injection Type)的更多相关文章

  1. 14.AutoMapper 之依赖注入(Dependency Injection)

    https://www.jianshu.com/p/f66447282780   依赖注入(Dependency Injection) AutoMapper支持使用静态服务定位构建自定义值解析器和自定 ...

  2. SQL注入(SQL Injection)案例和防御方案

    sql注入(SQL Injection):就是通过把SQL命令插入到Web表单递交或输入域名或页面请求的查询字符串,最终达到欺骗服务器执行恶意的SQL命令. SQL注入攻击的主要危害包括:非法读取.篡 ...

  3. 简明依赖注入(Dependency Injection)

    前言 这是因特奈特上面不知道第几万篇讲依赖注入(Dependency Injection)的文章,但是说明白的却寥寥无几,这篇文章尝试控制字数同时不做大多数. 首先,依赖注入的是一件很简单的事情. 为 ...

  4. spring之注入类型

    spring有三种注入类型: set注入: 构造注入: 接口注入: 一.set注入(引用spring官方文档中的例子)(用的最多) 1.首先在代码中我们需要编写成员变量的set方法,如下所示,一般情况 ...

  5. 控制反转Inversion of Control (IoC) 与 依赖注入Dependency Injection (DI)

    控制反转和依赖注入 控制反转和依赖注入是两个密不可分的方法用来分离你应用程序中的依赖性.控制反转Inversion of Control (IoC) 意味着一个对象不会新创建一个对象并依赖着它来完成工 ...

  6. html <input>标签类型属性type(file、text、radio、hidden等)详细介绍

    html <input>标签类型属性type(file.text.radio.hidden等)详细介绍 转载请注明:文章转载自:[169IT-最新最全的IT资讯] html <inp ...

  7. Swift编程语言学习12 ——实例方法(Instance Methods)和类型方法(Type Methods)

    方法是与某些特定类型相关联的函数.类.结构体.枚举都能够定义实例方法:实例方法为给定类型的实例封装了详细的任务与功能.类.结构体.枚举也能够定义类型方法:类型方法与类型本身相关联.类型方法与 Obje ...

  8. 读书笔记 effective c++ Item 19 像设计类型（type）一样设计

    1. 你需要重视类的设计 c++同其他面向对象编程语言一样,定义了一个新的类就相当于定义了一个新的类型(type),因此作为一个c++开发人员,大量时间会被花费在扩张你的类型系统上面.这意味着你不仅仅 ...

  9. C# 8中的范围类型(Range Type)

    C# 8.0中加入了一个新的范围类型(Range Type). 这里我们首先展示一些代码,并一步一步为代码添加一些不同的东西, 为大家展示一下范围类型的功能和用法. 我们最原始的代码如下: stati ...

随机推荐

  1. GDI绘图写的简单扫雷

    由于没话多少时间,这个扫雷我只实现了主要功能(扫雷功能,递归实现) 废话不多说,直接上代码 using System; using System.Collections.Generic; using ...

  2. [BZOJ 4923][Lydsy1706月赛]K小值查询

    传送门 势能分析平衡树,splay或treap都可以 放个指针版的就跑 #include <bits/stdc++.h> using namespace std; #define rep( ...

  3. SPOJ - DQUERY 莫队

    题意:给定\(a[1...n]\),\(Q\)次询问,每次统计\([L,R]\)范围内有多少个不同的数字 xjb乱写就A了,莫队真好玩 #include<iostream> #includ ...

  4. JAVA 使用Dom4j 解析XML

    [转自] http://blog.csdn.net/yyywyr/article/details/38359049 解析XML的方式有很多,本文介绍使用dom4j解析xml. 1.环境准备 (1)下载 ...

  5. python中变量，常量

    1.变量 变量的作用:一个变化的值 把程序运算的中间结果临时存到内存里,以备后面的代码继续调用,这几个名字的学名就叫做“变量“ 查看变量在内存中的位置用id(name) 变量定义规则: 变量名只能是 ...

  6. JavaEE 数据库随机值插入测试

    package com.jery.javaee.dbtest; import java.sql.Connection; import java.sql.DriverManager; import ja ...

  7. PIE SDK介绍

    1. 产品概述 PIE-SDK是航天宏图自主研发的PIE二次开发组件包,集成了专业的遥感影像处理.辅助解译.信息提取.专题图表生成.二三维可视化等功能.底层采用微内核式架构,由跨平台的标准C++编写, ...

  8. 有关tensorflow一些问题

    1.python版本 采用64位的python 2.系统不支持高版本tensorflow(>1.6),运行报错如下: 问题描述如下: ImportError: DLL load failed: ...

  9. Python-2.7 配置 tab 自动补全功能

    作者博文地址:http://www.cnblogs.com/liu-shuai/ 之前一直使用shell编程,习惯了shell的 tab 自动补全功能,而Python的命令行却不支持 tab 自动补全 ...

  10. HikariCP配置使用spring结合--Java数据库连接池

    我的个人德州扑克项目https://github.com/mingzijian/pokers,欢迎给星星.maven引入: Java 8 maven artifact: <dependency& ...