python集合、函数实例

集合

1、list ==》允许重复的集合，可修改
2、tuple ==》允许重复的集合，不可修改
3、dict ==》
4、set ==》不允许重复的集合，相当于不可重复的列表

set

是一个无序的且不重复的元素集合，不能通过下标取值
创建

s=set()
s={11,22,44,55}可以这样创建set

转换

s=set([11,22,22,333])#转换时自动忽略重复的
l=""
s=set(l)

s.add(33)添加一个元素
s.clear()清除元素

se={1,2,3,4}
b={4,4,4}
bb=se.difference(b)#找se中存在，b中不存在的的集合，需要用一个新的
#值接收
bb=se.difference_update(b)#找se中存在，b中不存在的的集合，并把值
#赋给se，不用赋给新的值（在原数据中更新）

se={1,2,3,4}
se.discart(5)移除，出错不报错
se.remove(5)移除，出错报错

se={1,2,3,4}
be={0,2,3,6}
ret=se.intersection(be)#取交集
print(ret)
se.intersection_update(be)#取交集在se中更新，（赋值给原数据）
ret=se.isdisjoint(be)#检测是不是无交集，有交集F，无T
se.issubset(be)#检测se是否为be的子集
se.issuperset(be)#检测se是否为be的父集（be是否为se的子集）
ret=se.pop()#ret为移除的值，由于set是无序的，所以删除最后一个值
#也是不确定的
ret=se.symmetrice(be)#把se中存在，be中不存的集合，和be中存在，se中不存
#在的集合赋值给ret（对称差集）
ret=se.symmetrice_difference_update（be）#在se中更新对称差集
ret=se.union(be)#取并集重复的只输出一个
se.update(be)#把be中的集合循环的添加到到se中
se.update([44,33,55])#把这个列表中的数据循环的添加到se中

例题old_dict={"#1":11,"#2":22,"#3":100,}
new_dict={"#1":33,"#4":22,"#7":100,}
将old_dict和new_dict都有的元素用new的更新old的
new_dict有的old_dict没有的添加到old中
将old_dict有的new_dict没有的删除

解题z

                old_dict={"#1":11,"#2":22,"#3":100,}
                new_dict={"#1":33,"#4":22,"#7":100,}
                old_keys=old_dict.keys()
                new_keys=new_dict.keys()

                old_set=set(old_keys)
                new_set=set(new_keys)

                del_set=old_set.difference(new_set)
                add_set=new_set.difference(old_set)
                ass=new_set.intersection(old_set)

                for i in old_set:
                    for k in del_set:
                        if i==k:
                            old_dict.pop(i)
                for i in old_dict.keys():
                    for k in ass:
                        if i==k:
                            old_dict[i]=new_dict[i]
                for i in add_set:
                    item={i:new_dict[i]}
                    old_dict.update(item)
                print(old_dict)
                print(ass)

三目运算，三元运算

if 1==1:
　　name="alex"
else:
　　name="eric"

name=值1 if 条件 else 值2
如果"条件"成立就把"值1"赋值给"name"
如果"条件"不成立就把"值2"赋值给"name"

name="alex" if 1==1 else "eric"
print(name)

#str,在内存中，一次性创建，不能被修改，只要修改，就在创建
#就是修改以后就重新创建一个，在指向这新创建的，而那个原来的还在
#只是不用了

#list，只要可以修改的，就是动态的，相当于链表，有下一个元素的位置
#和上一个元素的位置
#如果对列表里的元素进行里修改就重新创建一，它的索引禁指向新创建的
内容
a="alex"

浅拷贝

n1=123
import copy
n2=copy.copy(n1)
id<n1>
id<n2>

此时n1和n2的地址相同，字符串内部有优化机制

深拷贝

n1=123
import copy
n2=copy.deepcopy(n1)
id<n1>
id<n2>

此时n1和n2的地址也相同
数字、字符串
只要是拷贝，赋值
地址都一样

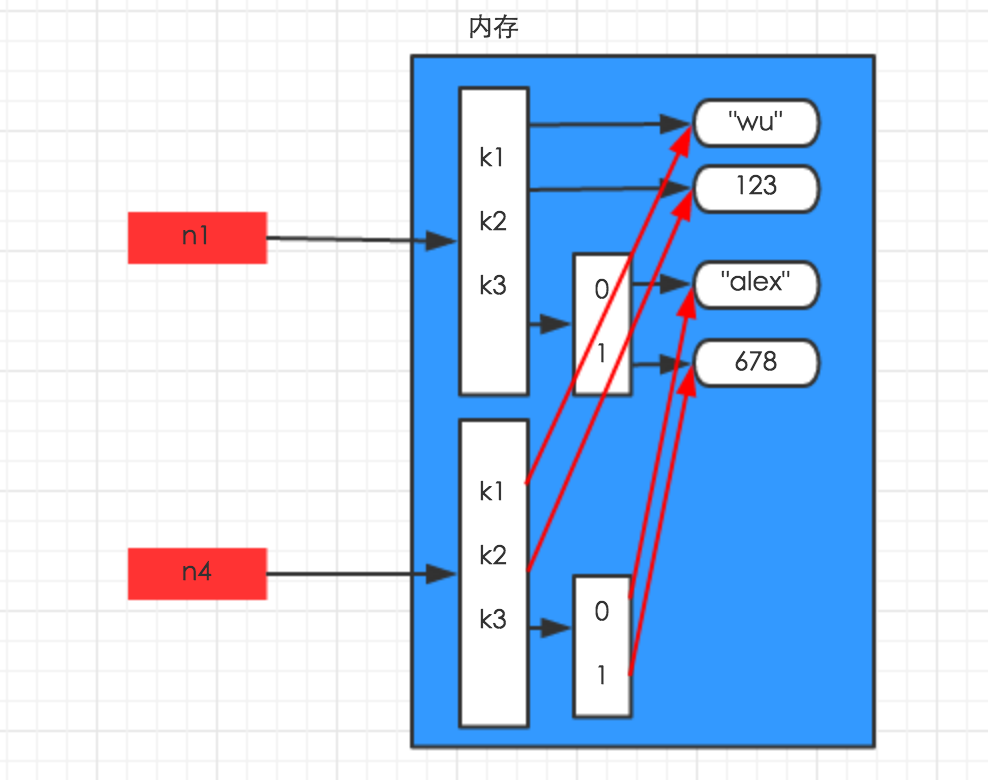
列表，字典，元素、、、、
深拷贝拷贝除了最里面那一层的所有层
浅拷贝拷贝最外面的那一层

过程式编程

函数式编程

创建一个函数

def xx():
　　print("alex")
　　return(可以是任意类型的值)
xx()

如果没有写返回值，这对一个函数赋值之后（a=xx()）则返回一个None给a
并不是像其他语言的函数一样不返回值

参数

def kd(p)
　　print(p) p为形参
　　return True

ret =kd("") 实参
print(ret)