一道组合数问题--出自 曹钦翔_wc2012组合计数与动态规划

一道组合数问题--出自 曹钦翔_wc2012组合计数与动态规划

【问题描述】

众所周知，xyc 是一个宇宙大犇，他最近在给他的学弟学妹们出模拟赛。

由于 xyc 实在是太巨了，他出了一套自认为很水的毒瘤模拟赛（看看这题的文件名你就

知道是什么难度了）。

这些题目对于选手来说实在是太 hard 了，愤怒的选手们在评测的时候蜂拥而上，把 xyc

抬了起来……在这一过程中，xyc 用于评测的电脑也被选手们给砸坏了。

尽管选手们的成绩极其惨淡，xyc 还是想研究一下选手们的分数分布情况，他尝试还原

出了电脑中的部分信息：

已知有 n 人参加这场模拟赛，共有 m 道题。现在模拟赛己经结束，评测正在进行中，

对于已经结束评测的试题，已知每名选手这道题的答案是否正确，对于未结束评测的试题，

只知道每名选手是否提交了代码。每个题分数固定，提交正解的选手可以得到这一题的分数

（由于比赛太毒瘤了，每一题没有任何部分分），分数越高排名越靠前，分数相同编号小的

选手排名靠前。

xyc 想知道如果要在排名最靠前的 s 人中选出 t 人，有多少种组合的可能。

xyc 认为这个问题太 naive 了，所以他就把这个问题丢给你了。

【输入格式】

输入文件第一行是 m，接下去 m 行每行一个整数来表示每道题目的分值（整数是正的

表示该题已经评测，否则表示该题尚未评测，该题目的分值为这个整数的绝对值）

然后是一个整数 n，接下去是一个 n 行 m 列的字母阵，字母阵只包含 YN 两种字母（Yes

or No）。如果第 i 题已经完成评测，那么这个字母矩阵中第 j 行第 i 列的字母表示第 j 名选

手的第 i 题是否已经得分；如果第 i 题尚未完成评测，那么这个字母矩阵中第 j 行第 i 列的

字母表示第 j 名选手的第 i 题是否提交了代码。

最后两行两个数字，分别为 s 和 t。

如果先选出s个再选出其中t个，可以写爆搜，需要判重比较难写。

不如直接枚举我们选哪t个。

那么就需要分析一波了。

我们需要维护每位选手可以得到分数的最大值和最小值。

这样就可以得出他们分数的大小关系。

先把选手按照第一关键字为最大分数第二关键字为编号的方式排序。

那么就可以得到一些东西，比如说：

​ 对于一个选手i，我们设他是t名里的最后一名，那么他的前面一共有i-1个人，这i-1个人中有t-1个在t名中（这是非常显然的）。

​ 那么我们对于每一个i，就可以去枚举他前面这i-1个人中哪t-1个人在t名中就可以了。

​ 怎么枚举，还有一个需要注意的地方。

​ 就是可能在1到i-1中可能有一些人满足：如果i在前t名，那么这些人必然在前t名。

​ 为什么？其实非常简单：因为这些人的最小分数可能大于i的最大分数。

那么我们就需要计算出究竟有多少个这样的人，这也是我们按照最大分数排序的原因，这样我们就可以将这些人弄在一起。

​ 具体如下图：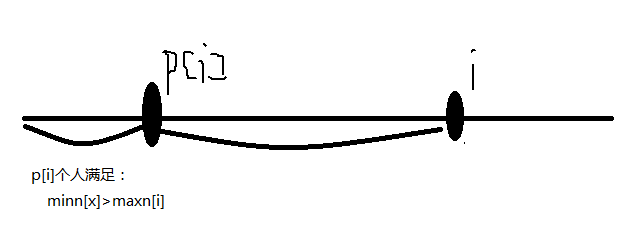

那么我们就成功地把1到i这一段线段分成了两段。

​ 这样之后我们就可以毫无顾虑的开始做数学了。

​ 我们要从这两段中一共选择t个人（第i个人必选）

​ 那么枚举一个量j设为在第一段中也就是前p[i]个人中有j个人被选中，那么就会有t-j-1个人在第二段也就是后\(i-1-p[i]\)被选中。

​ 直接组合数？

​ 并不，因为j还要有一些范围。

​ 1，\(j<=p[i]\)显然吧

​ 2，\(j<=t-1\)第i个人必选

​ 3，\(j>=p[i]+t-s\)，因为\(p[i]-j\)是第一段中不被选的，\(s-t\)是总共不会选的，那么就有:\(p[i]-j<=s-t\)

​ 4，\(p[i]+1<=s\)这样i才会在前s名中。

这样确定了j的范围之后，枚举j就可以了。

​ 即

\[ans=\prod_{j=max(0,p[i]+t-s)}^{max(p[i],t-1)}C(p[i],j)*C(i-p[i]-1,t-j-1)
\]

另外，求组合数不能用阶乘，用O(N)递推。

​ 即

\[C(n,i+1)=C(n,i)*(n-i)/(i+1)
\]

既然都会了，那就可以愉快地打代码了。

code：

#include <iostream>
#include <cstdio>
#include <algorithm>

using namespace std;

#define int long long

const int wx=117;

inline int read(){
	int sum=0,f=1; char ch=getchar();
	while(ch<'0'||ch>'9'){if(ch=='-')f=-1; ch=getchar();}
	while(ch>='0'&&ch<='9'){sum=(sum<<1)+(sum<<3)+ch-'0'; ch=getchar();}
	return sum*f;
}

struct node{
	int pts1,pts2; int flag,id;
	friend bool operator < (const node & a,const node & b){
		if(a.pts1==b.pts1)return a.id<b.id;
		return a.pts1>b.pts1;
	}
}a[wx],b[wx];

int n,m,T,S,ans;
int vis[wx],flag[wx],t[wx],tt[wx],p[wx];
char c[wx];

int Abs(int x){
	if(x<0)return -x;
	return x;
}

int C(int nn,int mm){
	if(nn<0||mm<0)return 0;
	if(mm==0)return 1;
	if(nn==0)return 0;
	if(nn==mm)return 1;
	if(mm>nn)return 0;
	int re=1;
	for(int i=0;i<nn-mm;i++){
		re=re*(nn-i)/(i+1);
	}
	return re;
}

signed main(){
	freopen("ctsc.in","r",stdin);
	freopen("ctsc.out","w",stdout);

	n=read();
	for(int i=1;i<=n;i++){
		int x=read();
		if(x>0)flag[i]=1;
		t[i]=Abs(x);
	}
	m=read();
	for(int i=1;i<=m;i++){
		scanf("%s",c+1);
		a[i].id=i;
		for(int j=1;j<=n;j++){
			if(flag[j])
				{
					if(c[j]=='Y')a[i].pts1+=t[j],a[i].pts2+=t[j];
				}
			else
				{
					if(c[j]=='Y')a[i].pts1+=t[j];
				}
		}
	}
	S=read(); T=read();
	sort(a+1,a+1+m);
	for(int i=1;i<=m;i++){
		for(int j=1;j<i;j++){
			p[i]+=((a[j].pts2>a[i].pts1)||(a[j].pts2==a[i].pts1&&a[j].id<a[i].id));
		}
	}
	for(int i=T;i<=m;i++){
		if(p[i]>S)break;
		int don=max(p[i]-S+T,(long long)0);
		int upp=min(p[i],T-1);
		for(int j=don;j<=upp;j++){
			ans+=C(p[i],j)*C(i-p[i]-1,T-j-1);
		}
	}

	printf("%lld\n",ans);
	return 0;
}