POJ 1039 Pipe【经典线段与直线相交】

链接：

http://poj.org/problem?id=1039

http://acm.hust.edu.cn/vjudge/contest/view.action?cid=22013#problem/B

Pipe

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 8350		Accepted: 2501

Description

The GX Light Pipeline Company started to prepare bent pipes for the new transgalactic light pipeline. During the design phase of the new pipe shape the company ran into the problem of determining how far the light can reach inside each component of the pipe.
Note that the material which the pipe is made from is not transparent and not light reflecting. 




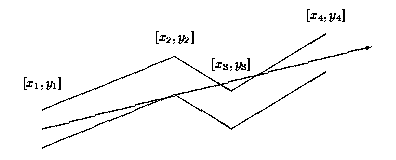
Each pipe component consists of many straight pipes connected tightly together. For the programming purposes, the company developed the description of each component as a sequence of points [x1; y1], [x2; y2], . . ., [xn; yn], where x1 < x2 < . . . xn . These
are the upper points of the pipe contour. The bottom points of the pipe contour consist of points with y-coordinate decreased by 1. To each upper point [xi; yi] there is a corresponding bottom point [xi; (yi)-1] (see picture above). The company wants to find,
for each pipe component, the point with maximal x-coordinate that the light will reach. The light is emitted by a segment source with endpoints [x1; (y1)-1] and [x1; y1] (endpoints are emitting light too). Assume that the light is not bent at the pipe bent
points and the bent points do not stop the light beam.

Input

The input file contains several blocks each describing one pipe component. Each block starts with the number of bent points 2 <= n <= 20 on separate line. Each of the next n lines contains a pair of real values xi, yi separated by space. The last block is denoted
with n = 0.

Output

The output file contains lines corresponding to blocks in input file. To each block in the input file there is one line in the output file. Each such line contains either a real value, written with precision of two decimal places, or the message Through all
the pipe.. The real value is the desired maximal x-coordinate of the point where the light can reach from the source for corresponding pipe component. If this value equals to xn, then the message Through all the pipe. will appear in the output file.

Sample Input

4
0 1
2 2
4 1
6 4
6
0 1
2 -0.6
5 -4.45
7 -5.57
12 -10.8
17 -16.55
0

Sample Output

4.67
Through all the pipe.

Source

Central Europe 1995

题意：

      给你一个管道,问是否能有这样一条光线从左到右边完整通过

       如果不能完整通过,则输出最远的相交点【x 最大】

算法：直线与线段相交【叉积】

思路：

           枚举上下端点成光线所在的直线即可

           看是否合法,如果合法：那么再看是否能够通过整个通道

            如果不能通过,则输出最远的 X

注意：

       判断线段和直线相交时,不能直接用两个叉积的积来判断

      【有可能光线早就跑到了管道外面,而你判断的确是没有交点,

      最后结果就变成了光线通过了整个通道,但是事实却并不是这样】

      所以，必须让光线和挡板【上下端点所成直线】相交,来确定光线确实在管道内

错误思想：

开始想着直线与线段只可能是下图的情况，那么直接用叉积的积判断直线和线段是否相交好了

                                                              

红色箭头的代表直线 AB,三条黑色线段代表所有的线段与直线 AB的关系【直线可以延伸,所以画一段没有关系】

那么如果是一般的情况，直接用直线和线段相交的代码判断就好了

/** 叉积*/
double Cross(Point A, Point B){
    return A.x*B.y - A.y*B.x;
}

/** Segment l1 cross Line l2*/
bool SegmentCrossLine(Line l1, Line l2) //Segment l1 cross Line l2
{
    return Cross(l1.s-l2.s,l2.e-l2.s)*Cross(l2.e-l2.s,l1.e-l2.s) > 0;
}

但是直接这样的裸判断无法判断下面这种情况,如果遇到下图的情况一开始光线就跑出了管道，那么永远不会有交点，那么如果放在我开始连样例都没有出的代码里面，就会直接输出

Through all the pipe.

然而事实并非这样。。。

那么如何解决：

方法一：

像第二个代码一样【kuangbin】先判断是否和挡板相交【也就是判断光线是否跑到管道外面】

尽量让光线和挡板相交就好了

如果当前遍历的端点所成的光线和前面所有的挡板【绿色部分】都相交,则光线合法

如果一条合法的光线也和后面的挡板都相交，那么光线能够通过后面的通道，也就是光线能够通过所有的光线

如果不能，则找出刚好不相交的挡板，看是从上面还是下面跑出去的，求出交点，更新最远的 X

方法二：

来自依然神的博客，不过还是KB神给我分析了上面的，我才想清楚的了

把管道上面的线段和管道下面的线段分开分析。

如果光线通过了这段管道，

那么上面的线段一定在光线上面，那么光线与上面的线段叉积就不会出现 < 0的情况

那么下面的线段也一定在光线下面，光线与下面的线段的叉积不会出现 > 0 的情况

【上面说的叉积，主要是看你程序具体中遍历的方向了】

参考博客：

KB神

依然神

/*************************************************************
B	Accepted	192 KB	47 ms	C++	2744 B
题意：给你一个管道,问是否能有这样一条光线从左到右边完整通过
       如果不能完整通过,则输出最远的相交点【x 最大】
算法：直线与线段相交【叉积】
思路：枚举上下端点成光线所在的直线即可
       看是否合法,如果合法：那么再看是否能够通过整个通道
       如果不能通过,则输出最远的 X
注意：判断线段和直线相交时,不能直接用两个叉积的积来判断
      【有可能光线早就跑到了管道外面,而你判断的确是没有交点,
      最后结果就变成了光线通过了整个通道,但是事实却并不是这样】
      所以，必须让光线和挡板【上下端点所成直线】相交,来确定光线确实在管道内
**************************************************************/
#include<stdio.h>
#include<math.h>
#include<algorithm>
using namespace std;

const int maxn = 30;
const double DNF = 100000000;
int n;
double ans;

struct Point{
    double x,y;
    Point() {}
    Point(double _x, double _y) {
        x = _x;
        y = _y;
    }

    Point operator + (const Point &B) const {
        return Point(x+B.x, y+B.y);
    }
    Point operator - (const Point &B) const {
        return Point(x-B.x, y-B.y);
    }
    Point operator * (const double &p) const {
        return Point(p*x, p*y);
    }
    bool operator == (const Point &B) const {
        return x == B.x && y == B.y;
    }
}up[maxn],down[maxn];
typedef Point Vector;

double Cross(Point A, Point B){
    return A.x*B.y - A.y*B.x;
}
/** 求直线 P+tv 和直线 Q+tw的交点 */
Point GetLineIntersection(Point P, Vector v, Point Q, Vector w){
    Vector u = P-Q;
    double t = Cross(w,u) / Cross(v,w);
    return P+v*t;
}

/** 精度判断 */
const double eps = 1e-5;
int dcmp(double x)
{
    if(fabs(x) < eps) return 0;
    else return x < 0 ? -1 : 1;
}

/** 检查直线 AB , 当前光线在第 e 段通道确定 */
bool check(Point A, Point B, int e){
    int sign = 0;
    int i;
    for(i = 1; i < n; i++)
    {
        if(dcmp(Cross(B-A, up[i]-A)) < 0  || dcmp(Cross(B-A,up[i+1]-A)) < 0)
        {//判断直线 AB 与线段 up[i] —— up[i+1]是否相交【注意】
            sign = 1; break;
        }

        if(dcmp(Cross(B-A,down[i]-A)) > 0 || dcmp(Cross(B-A,down[i+1]-A)) > 0 )
        {//判断直线 AB 与线段 down[i]——down[i+1]是否相交【注意】
            sign = 2; break;
        }

    }
    if(i < e) return false; //光线不合法
    if(i == n) return true; //通过整条通道
    //求最远的 x
    Point InterPoint;
    if(sign == 1) //与管道上面的线段相交
    {
        InterPoint = GetLineIntersection(A,A-B,up[i],up[i]-up[i+1]);
    }
    else if(sign == 2) //与管道下面的线段相交
    {
        InterPoint = GetLineIntersection(A,A-B,down[i],down[i]-down[i+1]);
    }
    //if(InterPoint == up[n] || InterPoint == down[n]) return true;
    ans = max(ans,InterPoint.x);
    return false;

}

int main()
{
    while(scanf("%d", &n) != EOF)
    {
        if(n == 0) break;

        double x,y;
        for(int i = 1; i <= n; i++)
        {
            scanf("%lf%lf", &x, &y);
            up[i] = Point(x,y);
            down[i] = Point(x,y-1);
        }

        ans = -DNF;
        int flag = 0; //标记是否能通过整条通道
        if(n < 3) flag = 1;
        for(int i = 1; i <= n && !flag; i++)
        {
            for(int j = i+1; j <= n; j++)
            {
                flag = check(up[i],down[j],i);
                if(flag) break;
                flag = check(down[i],up[j],i);
                if(flag) break;
            }
            if(flag) break;
        }
        if(flag) printf("Through all the pipe.\n");
        else printf("%.2lf\n", ans);
    }
    return 0;
}

Kuangbin大神的代码【先判断了是否和挡板相交，确定了光线在管道内，再直接用线段与直线相交求的】

http://www.cnblogs.com/kuangbin/p/3192590.html

#include <iostream>
#include <stdio.h>
#include <string.h>
#include <algorithm>
#include <queue>
#include <map>
#include <vector>
#include <set>
#include <string>
#include <math.h>

using namespace std;

const double eps = 1e-8;
int sgn(double x)
{
    if(fabs(x) < eps)return 0;
    if(x < 0)return -1;
    else return 1;
}
struct Point
{
    double x,y;
    Point(){}
    Point(double _x,double _y)
    {
        x = _x;y = _y;
    }
    Point operator -(const Point &b)const
    {
        return Point(x - b.x,y - b.y);
    }
    //叉积
    double operator ^(const Point &b)const
    {
        return x*b.y - y*b.x;
    }
    //点积
    double operator *(const Point &b)const
    {
        return x*b.x + y*b.y;
    }
    void input()
    {
        scanf("%lf%lf",&x,&y);
    }
};
struct Line
{
    Point s,e;
    Line(){}
    Line(Point _s,Point _e)
    {
        s = _s;e = _e;
    }
    //两直线相交求交点
    //第一个值为0表示直线重合，为1表示平行，为0表示相交,为2是相交
    //只有第一个值为2时，交点才有意义
    pair<int,Point> operator &(const Line &b)const
    {
        Point res = s;
        if(sgn((s-e)^(b.s-b.e)) == 0)
        {
            if(sgn((s-b.e)^(b.s-b.e)) == 0)
                return make_pair(0,res);//重合
            else return make_pair(1,res);//平行
        }
        double t = ((s-b.s)^(b.s-b.e))/((s-e)^(b.s-b.e));
        res.x += (e.x-s.x)*t;
        res.y += (e.y-s.y)*t;
        return make_pair(2,res);
    }
};
//判断直线和线段相交
bool Seg_inter_line(Line l1,Line l2) //判断直线l1和线段l2是否相交
{
    return sgn((l2.s-l1.e)^(l1.s-l1.e))*sgn((l2.e-l1.e)^(l1.s-l1.e)) <= 0;
}

Point up[100],down[100];
int main()
{
    int n;
    while(scanf("%d",&n) == 1 && n)
    {
        for(int i = 0;i < n;i++)
        {
            up[i].input();
            down[i] = up[i];
            down[i].y -= 1;
        }
        bool flag = false;//穿过所有的标记
        double ans = -10000000.0;
        int k;
        for(int i = 0;i < n;i++)
        {
            for(int j = i+1;j < n;j++)
            {
                //判断直线 up[i]——down[j]
                for(k = 0;k < n;k++) //判断是否跑到管道外面,应该和前面的所有的挡板相交
                    if(Seg_inter_line(Line(up[i],down[j]),Line(up[k],down[k])) == false)
                        break;
                if(k >= n) //通过了所有的挡板,光线可以射穿管道
                {
                    flag = true;
                    break;
                }
                if(k > max(i,j)) //如果光线合法
                {
                    if(Seg_inter_line(Line(up[i],down[j]),Line(up[k-1],up[k])))
                    {
                        pair<int,Point>pr = Line(up[i],down[j])&Line(up[k-1],up[k]);
                        Point p = pr.second;
                        ans = max(ans,p.x);
                    }
                    if(Seg_inter_line(Line(up[i],down[j]),Line(down[k-1],down[k])))
                    {
                        pair<int,Point>pr = Line(up[i],down[j])&Line(down[k-1],down[k]);
                        Point p = pr.second;
                        ans = max(ans,p.x);
                    }
                }

                //判断直线 down[i]——up[j]
                for(k = 0;k < n;k++)
                    if(Seg_inter_line(Line(down[i],up[j]),Line(up[k],down[k])) == false)
                        break;
                if(k >= n)
                {
                    flag = true;
                    break;
                }
                if(k > max(i,j))
                {
                    if(Seg_inter_line(Line(down[i],up[j]),Line(up[k-1],up[k])))
                    {
                        pair<int,Point>pr = Line(down[i],up[j])&Line(up[k-1],up[k]);
                        Point p = pr.second;
                        ans = max(ans,p.x);
                    }
                    if(Seg_inter_line(Line(down[i],up[j]),Line(down[k-1],down[k])))
                    {
                        pair<int,Point>pr = Line(down[i],up[j])&Line(down[k-1],down[k]);
                        Point p = pr.second;
                        ans = max(ans,p.x);
                    }
                }
            }
            if(flag)break;
        }
        if(flag)printf("Through all the pipe.\n");
        else printf("%.2lf\n",ans);
    }
    return 0;
}