POJ 3734 生成函数
题意:一排n长度的砖,有四种颜色,红色绿色是偶数,有少染色方式。
分析:
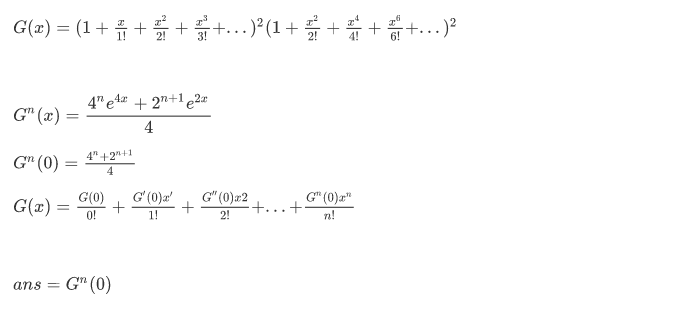
泰勒展开式:
chx = (e^x+e^(-x))/2 = 1 + x^2/2! + x^4/4! + x^6/6! + ... ...
shx = (e^x-e^(-x))/2 = x + x^3/3! + x^5/5! + x^7/7! + ... ...
POJ 3734 生成函数的更多相关文章
- poj 3734 Blocks【指数型生成函数】
指数型生成函数,推一推可得: \[ (1+\frac{x^1}{1!}+\frac{x^2}{2!}+\frac{x^3}{3!}+...)^2+(1+\frac{x^2}{2!}+\frac{x^4 ...
- [POJ 3734] Blocks (矩阵高速幂、组合数学)
Blocks Time Limit: 1000MS Memory Limit: 65536K Total Submissions: 3997 Accepted: 1775 Descriptio ...
- poj 3734 Blocks
ゲート 分析:这题过的人好多,然后大家好像是用矩阵过的(((φ(◎ロ◎;)φ))).我自己是推公式的. 对于任意的有这个式子, 就是先从里面选偶数个涂成两个指定的颜色,再在选出的里面选定涂某种颜色,选 ...
- poj 3734 Blocks 快速幂+费马小定理+组合数学
题目链接 题意:有一排砖,可以染红蓝绿黄四种不同的颜色,要求红和绿两种颜色砖的个数都是偶数,问一共有多少种方案,结果对10007取余. 题解:刚看这道题第一感觉是组合数学,正向推了一会还没等推出来队友 ...
- poj 3734 矩阵快速幂+YY
题目原意:N个方块排成一列,每个方块可涂成红.蓝.绿.黄.问红方块和绿方块都是偶数的方案的个数. sol:找规律列递推式+矩阵快速幂 设已经染完了i个方块将要染第i+1个方块. a[i]=1-i方块中 ...
- POJ 3734
题目的大意: 给定待粉刷的n个墙砖(排成一行),每一个墙砖能够粉刷的颜色种类为:红.蓝.绿.黄, 问粉刷完成后,红色墙砖和蓝色墙砖都是偶数的粉刷方式有多少种(结果对10007取余). 解题思路: 思路 ...
- Blocks(POJ 3734 矩阵快速幂)
Blocks Input The first line of the input contains an integer T(1≤T≤100), the number of test cases. E ...
- poj 3734 方块涂色 求红色 绿色方块都为偶数的方案数 (矩阵快速幂)
N个方块排成一列 用红,蓝,绿,黄4种颜色去涂色,求红色方块 和绿色方块个数同时为偶数的 方案数 对10007取余 Sample Input 212Sample Output 2//(蓝,黄)6//( ...
- POJ 3734 Blocks (矩阵快速幂)
题目链接 Description Panda has received an assignment of painting a line of blocks. Since Panda is such ...
随机推荐
- 小众软件:Windows 下优化软件推荐—— Dism++ | 强迫症晚期患者福音 - 少数派
Windows 下优化软件推荐—— Dism++ | 强迫症晚期患者福音 - 少数派 https://sspai.com/post/41992 官方网站免费下载
- 《阿里如何实现秒级百万TPS?搜索离线大数据平台大数据平台架构解读》读后感
在使用淘宝时发现搜索框很神奇,它可以将将我们想要的商品全部查询出来,但是我们并感觉不到数据库查询的过程,速度很快.通过阅读这篇文章让我知道了搜索框背后包含着很多技术,对我以后的学习可能很有借鉴. 平时 ...
- Ubuntu安装Docker步骤
环境:Ubuntu Trusty 14.04 (LTS) 前提条件: Docker requires a 64-bit installation regardless of your Ubuntu v ...
- springboot 之 使用jetty web容器
springboot 中默认的web容器是tomcat. 在maven 的pom 文件中加入如下依赖,便可使用tomcat 容器. <dependency> <groupId> ...
- HZAU 18——Array C——————【贪心】
18: Array C Time Limit: 1 Sec Memory Limit: 128 MBSubmit: 586 Solved: 104[Submit][Status][Web Boar ...
- Python高级用法------字典无需提前定义key
from collections import defaultdict import json def tree(): return defaultdict(tree) categories = tr ...
- 【linux相识相知】独立硬盘冗余阵列-RAID
独立硬盘冗余阵列(RAID,Redundant Array of Independant Disks),旧称为廉价磁盘冗余阵列(Redundant Array of Inexpensive Disks ...
- 微信小程序参考资料及网址
微信小程序 https://mp.weixin.qq.com/debug/wxadoc/dev/api/ http://www.w3cschool.cn/weixinapp/ 微信小程序 开发工具 h ...
- JavaScript 监听回车事件
JS监听某个输入框 //回车事件绑定 $('#search_input').bind('keyup', function(event) { if (event.keyCode == "13& ...
- Git for Android Studio 学习笔记
http://learngitbranching.js.org/ 一个特别好的git学习教程 创建一个project,然后导入github
