神秘值分解（Singular Value Decomposition）

- 线性变化的几何表现

• 首先看下简单的矩阵，这是一个对角矩阵
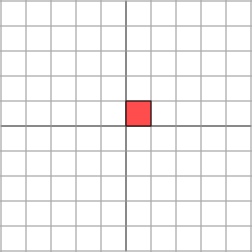
  M=(3001)

  我们先用这个对角矩阵乘以一个点来看看它的几何变化。

  (3001)∗(xy)=(3xy)

  在几何上就相当于把原来的向量x轴方向拉伸成了原来的3倍
  
  –》

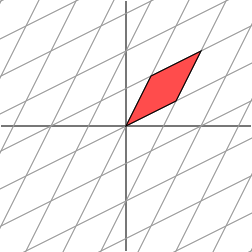
• 再来看下对称矩阵

  M=(2112)

  利用对称矩阵乘以一个点来看看它的几何变化

  -》
  
  这并不能清晰的显示出发生了如何的几何变换。我们能够把整个坐标轴逆时针旋转45度来更好的发现规律。
  
  -》
  
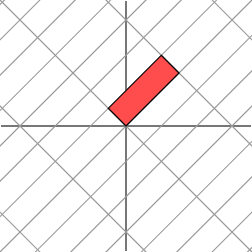
  从上图能够看出原来的红色部分。沿着一个方向被拉伸了3倍。

- 神秘值分解

这是神秘值分解的几何实质：对于随意的二维方阵（M）,我们都能够找到相互正交的向量 （v1,v2），使得经过M变换后得到的两个向量(Mv1,Mv2)还是正交的。

-》

 v1和v2是正交的单位向量 u1和u2是在Mv1和Mv2方向上的单位向量σ1和σ2表示v1和v2经过M变换后的拉伸倍数Mv1=σ1u1Mv2=σ2u2

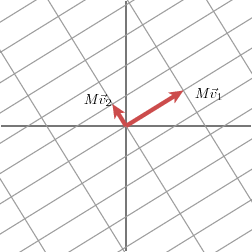
对于随意的二维向量x

x=(v1.x)v1+(v2.x)v2Mx=(v1.x)Mv1+(v2.x)Mv2Mx=(v1.x)σ1u1+(v2.x)σ2u2由于v.x=vTxMx=u1σ1vT1x+u2σ2vT2xM=u1σ1vT1+u2σ2vT2M=UΣVTU=(u1u2)Σ=(σ100σ2)V=(v1v2)

-那么我们怎么发现神秘值呢

我们能够对不论什么矩阵进行神秘值分解，首先我们先看下最先的样例，我们在原来的红色正方形上加上一个单位圆

-》

变化后的图形是个椭圆。我们我们能够在椭圆的最长和最短的方向上发现正交基

-》

我们可以发现vi和vj是MTM的特征向量，因为MTM是一个对称矩阵那么不同特征值所对应的特征向量都是正交的所以vTivj=0,奇异值σi=|Mvi|ui是Mvi方向上的单位向量，问题是为什么ui和uj是正交的呢？我们假设σi和σj是不同的奇异值Mvi=σiuiMvj=σjuj.(Mvi)TMvj=vTiMTMvj=vTiλvj=λvTivj=0.(Mvi)TMvj=(σiui)Tσjuj=0uTiuj=0ui和uj正交所以我们发现了一系列的正交的vi经过M变换后成为ui。uiuj还是正交的

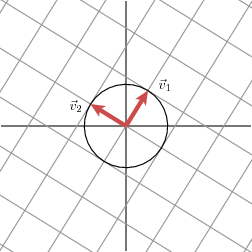- 另外一个样例

M=(1212)

利用M对v1 v2进行变换

-》

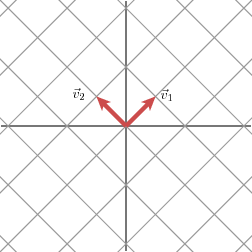在这个样例中第二个神秘值为0,

M=u1σ1vT1

M的秩是等于非0的神秘值的数目的。

- 数据压缩

神秘值分解能够有效地应用在数据表示中，如果我们来表示一个25*15的黑白像素



由于在整个图像中仅仅有3种列向量。所以我们能够来表示图像更加地高效



我们用一个25*15的矩阵来表示这个图像，1表示白色，0表示黑色



我们对M进行神秘值分解。仅仅发现了3个非0的神秘值

σ1=14.72σ2=5.22σ3=3.31M=u1σ1vT1+u2σ2vT2+u3σ3vT3ui是一个25维的向量vi是15维的向量我们用了非常少的数据量就把刚刚的M矩阵表示了

-噪音处理

如果我们利用了一个扫描器来扫描图像。可是在扫描的过程中引入了噪声



我们对这个25*15的矩阵进行神秘值分解

σ1=14.15σ2=4.67σ3=3.00σ4=0.21σ5=0.19...σ15=0.05M近似表示为M=u1σ1vT1+u2σ2vT2+u3σ3vT3