（原创）像极了爱情的详解排序二叉树，一秒get

排序二叉树（建立、查找、删除）

二叉树我们已经非常熟悉了，但是除了寻常的储存数据、遍历结构，我们还能用二叉树做什么呢？

我们都知道不同的遍历方式会对相同的树中产生不同的序列结果，排序二叉树就是利用二叉树的遍历特征实现的特殊树种，也叫二叉查找树。

1. 排序二叉树从根结点起的每一个结点的左子树元素均小于其自身，右子树元素值均大于其自身
2. 即任何结点的值均大于其左子树所有元素，均小于其右子树所有元素

如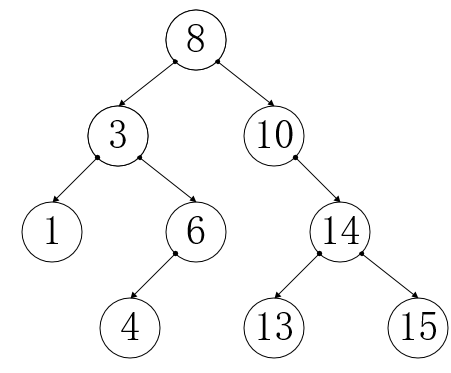：就是一个排序二叉树，直观的一批，从子树到根结点，永远符合左小右大的规则（中序遍历）

Ⅰ、结构定义

排序二叉树的定义与一般二叉树无异

typedef struct BiTree{
    int item;
    struct BiTree *lchild,*rchild;
}BiTree;

Ⅱ、排序二叉树的查找

我们先来看一下排序二叉树的查找实现，因为插入在排序二叉树中是实现后续建立、删除结点的基础，因为结点带有顺序，故而遍历条件有所改变，代码如下：

int searchnode(BiTree *t, int key)
{
    if(!t)
        return ;
    if(t->item == key)
    {
        return ;
    }
    else
    {
        if(t->item > key)
            return searchnode(t->lchild,key);
        if(t->item < key)
            return searchnode(t->rchild,key);
    }
}

清爽递归，不解释

Ⅲ、二叉排序树的插入

void insertbitree(BiTree **t, int value)
{
    if(!searchnode(*t,value))
    {
        if(*t == NULL)
        {
            *t = (BiTree *)malloc(sizeof(BiTree));
            (*t)->item = value;
            (*t)->lchild = NULL;
            (*t)->rchild = NULL;
        }
        else
        {
            if((*t)->item > value)
                insertbitree(&((*t)->lchild), value);
            else
                insertbitree(&((*t)->rchild), value);
        }
    }
}

这个插入上来先判断一哈我们现有的树里面有没有这个元素，如果有就不会进入循环，至于插入操作的框架也基本符合中序遍历的操作，只是加上了判断大小

Ⅳ、二叉排序树删除结点（HARD）

轻松愉快的建立、查找排序二叉树的操作完成之后，我们来看看比较困难的删除排序二叉树结点的操作。为什么说它困难呢，相比插入或者查找，删除面对的是一个已经成型的树，我们不仅要考虑怎样去掉这个结点，还要想到按照中序以及数字大小将原有结点按序放到正确位置。

好的，我们先来考虑一下我们可能删除哪几种结点：

第一类：待删除结点只有左子树，没有右子树，可以想见，这种情况下只需要把后续的左子树接到待删除结点的上一个结点上，再释放待删除结点的空间就OK

第二类：带删除结点只有右子树，没有左子树，跟第一类一个道理，这样的操作只需要三行就解决，但是棘手的问题总在短暂的轻松过后

第三类：这一类情况就是大魔王辽，左右孩子一个不缺，手心手背都是肉，哪个也不能少，怎么解决这个问题呢？让我们来看一个例子。

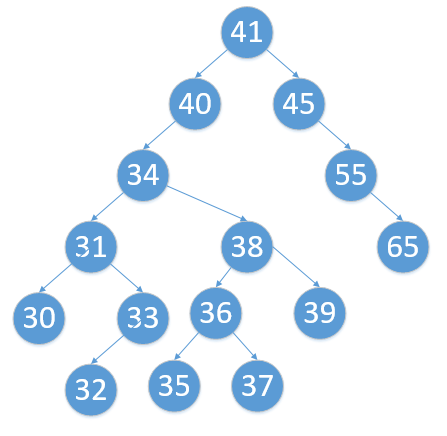看这个丑不拉叽的排序二叉树，非常体现中序遍历特点

现在我们要删除 34 这个结点，就是我们刚才说的那种第三类情况，左右均有结点，这个时候，我们有这两种方法阔以达成目的

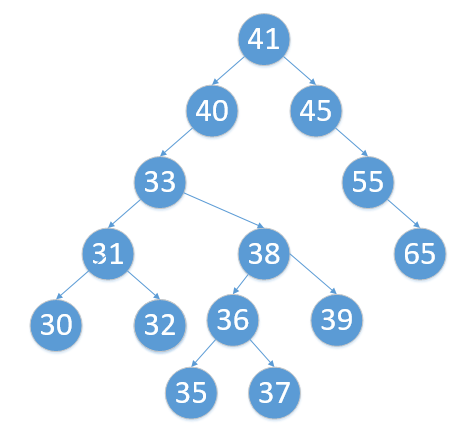
第一种：姑且叫他 牺牲前驱法 ，我们要去掉 34 ，就要把他的前驱拿来顶替这个位置，保持二叉排序树的序，然后当然要检测一下，如果牺牲的这个前驱点（在我们这里是 33 ）有子树，还需要把子树和上一级连上（如32），这是第一种方法

1. 用直接前驱 33 替换 34 
2. 删除原有的 33 结点
3. 把结点 32 ，移到原 33 位置

第二种：相信你也猜到了，牺牲后继法，反正兄弟两个要挑一个顶上去，让我们看一哈在这个例子中，怎么个牺牲后继

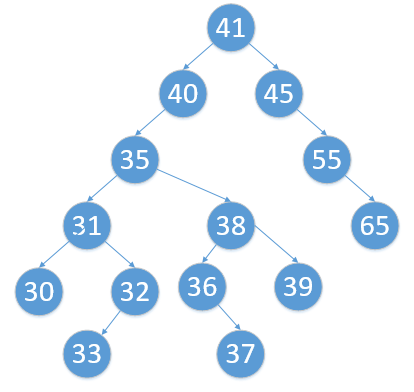
35 已经被我们放上来辽

1. 用直接后继 35 替换 34
2. 删除结点 35 

因为这里的 35 茕茕孑立，没儿没女，所以这个例子的这里不需要连接子树，但是千万注意不要认为所有的替换后继法都不用管子树

好的，方法讲明白了辽，我们代码实现一哈

int Delete(BiTree **t)
{
    BiTree *s,*q;
    if((*t) -> lchild == NULL)//左子树空的情况
    {
        q = *t;
        *t = (*t)->lchild;
        free(q);
    }
    else if( (*t) -> rchild == NULL)//右子树为空的情况
    {
        q = *t;
        *t = (*t)->rchild;
        free(q);
    }
    else //左右子数均为空
    {
        q = *t;
        s = (*t)->lchild;
        while(s->rchild)//循环找到直接前驱
        {
            q = s;
            s = s->rchild;
        }
        (*t) -> item = s -> item; //结点数据替换
        if(q != *t) //接原有左右子树
            q->rchild = s->lchild;
        else
            q->lchild = s->lchild;
        free(s);
    }
    return ;
}
int DeleteBST(BiTree **T, int key)
{

    if (!*T)
        return ;
    else
    {
        if (key ==  (*T)->item)
            return Delete(T);
        else if (key < (*T)->item)
            return DeleteBST(&(*T)->lchild, key);
        else
            return DeleteBST(&(*T)->rchild, key);
    }
    return ;
}

解读见注释

测试用主函数部分：

int main()
{
    int i;
    BiTree *t = NULL;
    int value[] = {,,,,,,,,,};
    for(i = ; i < ; i++)
        insertbitree(&t,value[i]);
    printf("建立序列为：\n");
    lar(t);
    printf("\n");
    printf("删除结点88，结果为：\n");
    DeleteBST(&t,);
    lar(t);
    printf("\n");
    return ;
}

呼~完毕