【LeetCode】【动态规划】Edit Distance

描述

Given two words word1 and word2, find the minimum number of operations required to convert word1 to word2.

You have the following 3 operations permitted on a word:

1. Insert a character
2. Delete a character
3. Replace a character

Example 1:

Input: word1 = "horse", word2 = "ros"
Output: 3
Explanation:
horse -> rorse (replace 'h' with 'r')
rorse -> rose (remove 'r')
rose -> ros (remove 'e')

Example 2:

Input: word1 = "intention", word2 = "execution"
Output: 5
Explanation:
intention -> inention (remove 't')
inention -> enention (replace 'i' with 'e')
enention -> exention (replace 'n' with 'x')
exention -> exection (replace 'n' with 'c')
exection -> execution (insert 'u')

思路：动态规划

这是一个经典的动态规划问题，思路参考斯坦福的课程：http://www.stanford.edu/class/cs124/lec/med.pdf

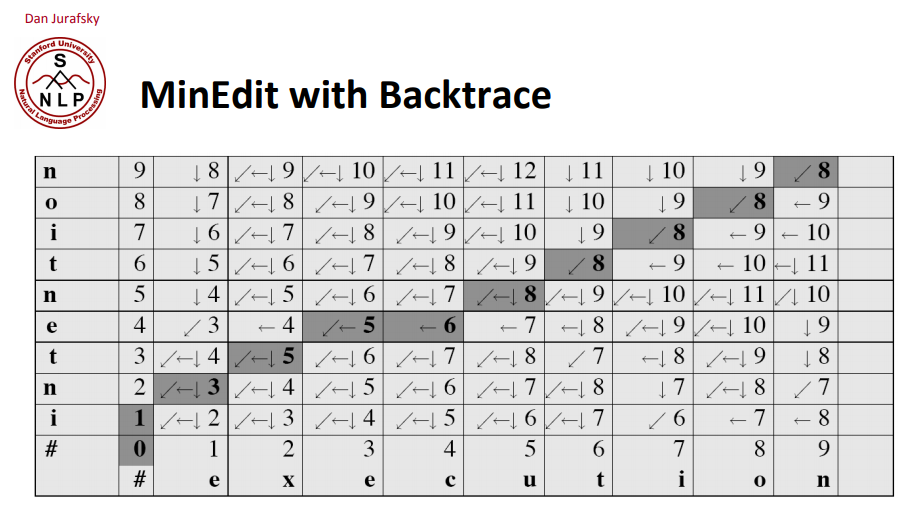
这里把加2变成加1即可

1. dp[i][0] = i;
2. dp[0][j] = j;
3. dp[i][j] = dp[i - 1][j - 1], if word1[i - 1] = word2[j - 1];
4. dp[i][j] = min(dp[i - 1][j - 1] + 1, dp[i - 1][j] + 1, dp[i][j - 1] + 1), otherwise.

class Solution {
public:
    int minDistance(string word1, string word2) {
        int m = word1.size(), n = word2.size();
        vector<vector<int> > dp(m+, vector<int>(n+, ));
        for(int i = ;i<=m;++i)
            dp[i][] = i;
        for(int i = ;i<=n;++i)
            dp[][i] = i;
        for(int i = ;i<=m;++i){
            for(int j = ;j<=n;++j){
                if(word1[i-] == word2[j-])
                    dp[i][j] = dp[i-][j-];
                else
                    dp[i][j] = min(dp[i-][j-], min(dp[i][j-], dp[i-][j])) + ;
            }
        }
        return dp[m][n];
    }
};